树的基本概念

在数据结构中，树（Tree）是一种层次结构，由节点和边组成。树的基本概念包括根节点、子节点、父节点、兄弟节点等。节点拥有零个或多个子节点，除了根节点外，每个节点有且仅有一个父节点。树的层数称为树的高度。子节点以及它后续节点所形成的数称为子树。

1.二叉树（Binary Tree）

二叉树是一种特殊的树结构，每个节点最多有两个子节点，分别称为左子节点和右子节点。

二叉树的基本概念：

1. 节点（Node）： 二叉树的基本构建单元，包含数据元素以及指向左右子节点的指针。

2. 根节点（Root）： 树的顶端节点，没有父节点。

3. 叶子节点（Leaf）： 没有子节点的节点称为叶子节点。

4. 父节点、子节点、兄弟节点： 一个节点的直接上级是其父节点，直接下级是其子节点。具有相同父节点的节点互为兄弟节点。

5. 深度（Depth）： 节点的深度是从根节点到该节点的路径长度，根节点的深度为0。

6. 高度（Height）： 节点的高度是从该节点到其最远叶子节点的路径长度，叶子节点的高度为0。

二叉树有以下几种特殊形态：

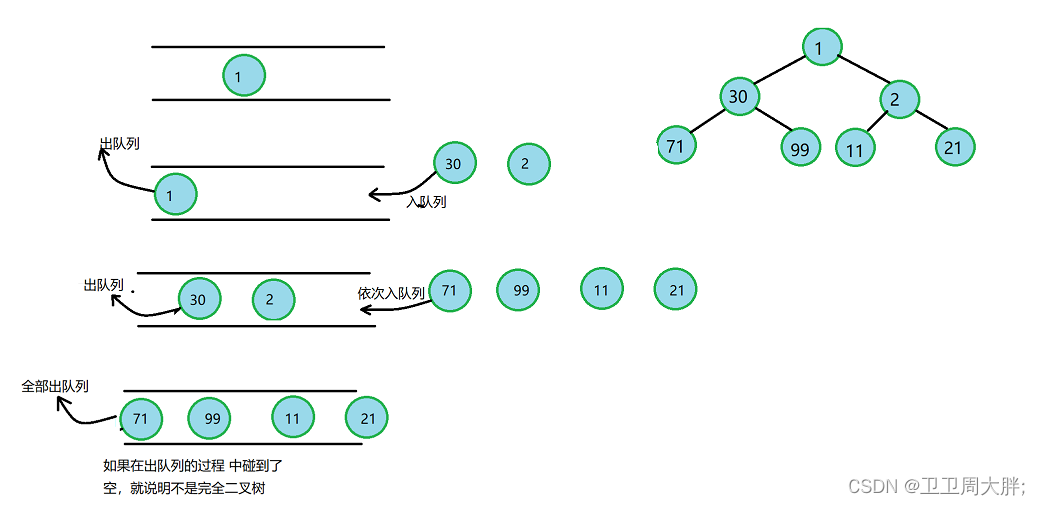
1.1完全二叉树（Complete Binary Tree）

除了最后一层外，其他层的节点都是满的，且最后一层的节点从左到右连续排列。最后一层空缺的节点必须在右边，左边必须填满。

1.2满二叉树（Full Binary Tree）

每个节点要么没有子节点，要么有两个子节点。

1.3完美二叉树（Perfect Binary Tree）

所有叶子节点都在同一层，且每个非叶子节点都有两个子节点。

2.平衡二叉树（Balanced Binary Tree）

平衡二叉树是一种特殊的二叉树，它的左子树和右子树的高度差不超过1。常见的平衡二叉树有AVL树和红黑树。

3.二叉搜索树（Binary Search Tree）

二叉搜索树是一种有序的二叉树，对于每个节点，其左子树的值都小于该节点的值，右子树的值都大于该节点的值。这种特性使得在二叉搜索树中进行查找、插入和删除操作非常高效。

4.自平衡二叉搜索树

自平衡二叉搜索树是一种特殊的二叉搜索树，它在插入或删除节点时会自动调整树的结构，以保持树的平衡性。常见的自平衡二叉搜索树有红黑树和AVL树。

• AVL树（AVL Tree）:
  

AVL树是一种高度平衡的二叉搜索树，它的每个节点都有一个平衡因子（Balance Factor），表示其左子树高度和右子树高度之差。AVL树满足以下性质：

1. 每个节点的平衡因子只能是-1、0或1。
2. 对于每个节点，其左子树和右子树的高度差的绝对值不超过1。

AVL树通过对节点进行旋转操作来保持树的平衡性。当插入或删除节点后，如果破坏了平衡性，AVL树会进行旋转操作来调整节点的位置，使得树重新平衡。相比于红黑树，AVL树的平衡性更加严格，因此在某些场景下，AVL树的查询效率可能更高。

• 红黑树（Red-Black Tree）:
  

红黑树是一种具有自平衡性质的二叉搜索树。它的每个节点都有一个颜色属性，可以是红色或黑色。红黑树满足以下几个性质：

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 每个叶子节点（NIL节点，空节点）是黑色。
4. 如果一个节点是红色，则它的两个子节点都是黑色。
5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数量的黑色节点。

通过这些性质，红黑树可以保持树的平衡，使得树的高度相对较小，从而提高了查找、插入和删除操作的效率。红黑树的插入和删除操作可能需要进行旋转和颜色调整来保持平衡性。

一般来说，红黑树适用于插入和删除操作较多的场景，而AVL树适用于对查询操作有更高要求的场景。

二叉树的应用：

1. 搜索和排序： 二叉搜索树可以用于快速搜索和排序。

2. 表达式树： 二叉树可以用于表示数学表达式，便于求值和转换。

3. 文件系统： 文件系统中的目录结构通常可以用二叉树表示。

4. 哈夫曼树： 用于数据压缩算法中，构建最优编码树。

5. 数据库索引： 数据库中的索引通常使用二叉树结构。

5.三叉树（Ternary Tree）

三叉树是一种每个节点最多有三个子节点的树结构。它可以用于表示多叉树的一种特殊情况。

6.多叉树（Multiway Tree）

多叉树是一种每个节点可以有多个子节点的树结构。每个节点的子节点数量可以是任意的。

---

图片来源：峰华前端工程师