【算法系列篇】递归、搜索和回溯（四）

在这里插入图片描述

文章目录

前言
什么是决策树
1. 全排列
- 1.1 题目要求
- 1.2 做题思路
- 1.3 代码实现
2. 子集
- 2.1 题目要求
- 2.2 做题思路
- 2.3 代码实现
3. 找出所有子集的异或总和再求和
- 3.1 题目要求
- 3.2 做题思路
- 3.3 代码实现
4. 全排列II
- 4.1 题目要求
- 4.2 做题思路
- 4.3 代码实现

前言

前面我们通过几个题目基本了解了解决递归类问题的基本思路和步骤，相信大家对于递归多多少少有了更加深入的了解。那么本篇文章我将为大家分享结合决策树来解决递归、搜索和回溯相关的问题。

什么是决策树

决策树是一种基本的分类与回归方法。在分类问题中，决策树通过构建一棵树形图来对数据进行分类。树的每个节点表示一个特征属性，每个分支代表一个特征属性上的判断条件，每个叶节点代表一个类别。在回归问题中，决策树可以预测一个实数值。

下面是一个简单的决策树：
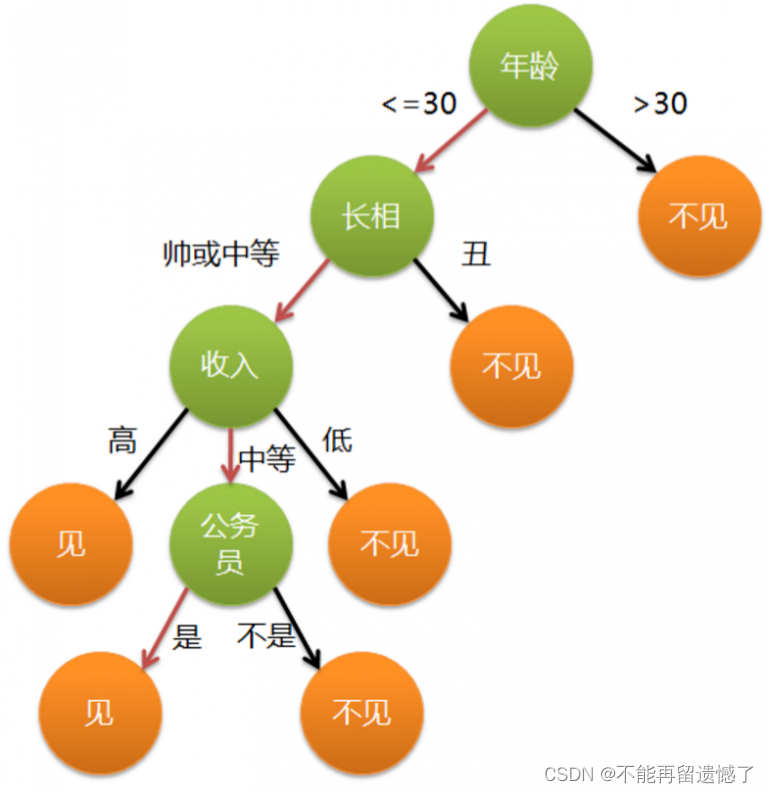
在这里插入图片描述
知道了什么是决策树，下面我们将运用决策树来解决实际问题。

1. 全排列

https://leetcode.cn/problems/permutations/

1.1 题目要求

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

class Solution {
    public List<List<Integer>> permute(int[] nums) {

    }
}

1.2 做题思路

相信大家肯定做过跟排列相关的问题，就是三个人坐座位的问题。第一座位可以坐A、B、C 任何一个人，如果第一个座位坐的是 A 的话，那么第二个位子 A 就不能再坐了，第二个位子就只能在 B、C 之间选择了，如果 B 选择了第二个位子，那么第三个位置就只能 C 选择了。所以这个问题通过决策树来体现的话就是这样的：

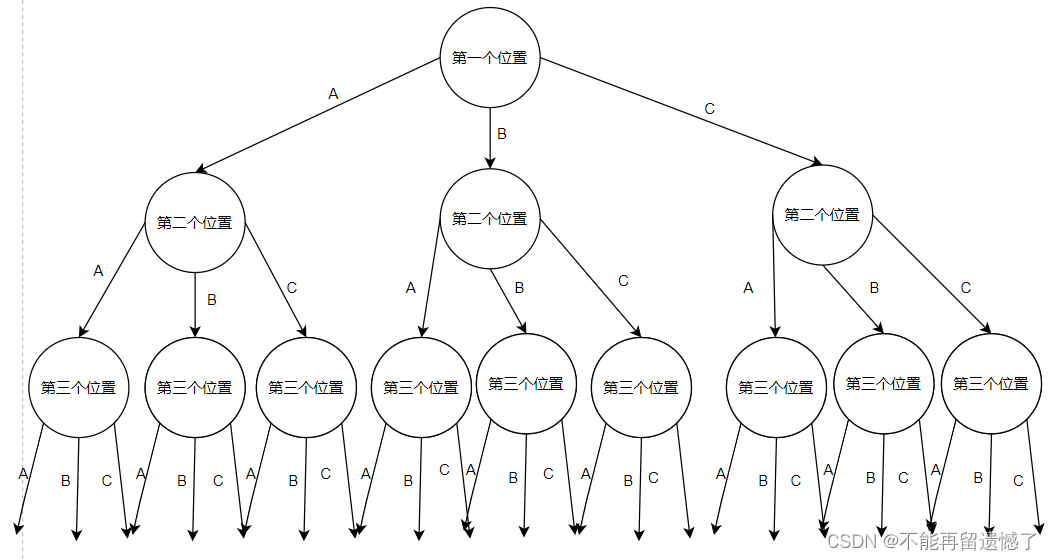
在这里插入图片描述
但是上面的图我们会发现这几种情况会有重复的情况，那么我们如何筛选掉这些重复的情况呢？可以使用一个标记数组来记录已经选择过的元素，当下一次选择的时候就选择这个标记数组中没有被选择的剩下的元素的其中一个。这道题目跟上面的例子的思路是一样的，这里我就不为大家再画一个图了。

那么这道题使用代码的思想该如何解决呢？每次递归我们还是将数组中的所有元素都给列举出来，不过我们需要根据标记数组中元素的使用情况来选择是否可以选择这个元素，如果某个元素没有被选择，那么这次就选择这个元素，将这个元素标记为已使用，然后继续递归，当当前情况列举完成之后就需要恢复现场，当路径集合中记录的元素的个数和数组中的元素个数相同的时候，就说明一种情况已经列举完成，就可以将当前情况添加进ret集合中，返回。

1.3 代码实现

class Solution {
    List<Integer> path;
    List<List<Integer>> ret;
    boolean[] vis;
    public List<List<Integer>> permute(int[] nums) {
        //对全局变量进行初始化
        path = new ArrayList<>();
        ret = new ArrayList<>();
        vis = new boolean[nums.length];
        dfs(nums);
        return ret;
    }

    private void dfs(int[] nums) {
    	//当path中元素的大小等于数组的大小，就说明一种情况已经列举完成，这事需要我们将当前path中的数据添加进ret中，并且返回
        if (path.size() == nums.length) {
            ret.add(new ArrayList<>(path));
            return;
        }
       for (int i = 0; i < nums.length; i++) {
           if (vis[i] == false) {
               path.add(nums[i]);
               //将当前元素标记为已使用
               vis[i] = true;
               //考虑该位置之后的其他元素的选择
               dfs(nums);
               //恢复现场
               path.remove(path.size() - 1);
               vis[i] = false;
           }
       }
    }
}

在这里插入图片描述

2. 子集

https://leetcode.cn/problems/subsets/

2.1 题目要求

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按任意顺序返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

class Solution {
    public List<List<Integer>> subsets(int[] nums) {

    }
}

2.2 做题思路

前面全排列中是当路径集合中的元素个数和数组中的元素的个数相同的时候视为一种情况，这道题目就不一样了，这个是数组的子集，也就是说每一种情况的元素的个数可能是不一样的，所以我们路径集合每新添加一个元素就可以视为一种情况，就需要将路径中的元素添加进ret集合中，思路跟上一道题目是类似的，都是通过决策树递归来实现的，但是呢？仔细看题目可以发现，就是集合[1,2]，[2,1]是一种情况，也就是说子集的选择跟顺序无关，那么我们又该如何避免出现重复的情况呢？

这其实也不难，想想如果是在数学中我们会怎样思考？如果当前位置我们选择了某个元素，那么后面的位置我们就从这个元素的后面元素中去选择。

在这里插入图片描述
所以通过代码体现的话，就是我们可以使用一个 pos 变量来记录当前位置选择的元素的下标，然后下一个位置选择元素递归的话，我们就从 pos 的下一个位置开始选择。

2.3 代码实现

class Solution {
    List<Integer> path;
    List<List<Integer>> ret;
    public List<List<Integer>> subsets(int[] nums) {
        path = new ArrayList<>();
        ret = new ArrayList<>();
        dfs(nums, 0)
        return ret;
    }

    private void dfs(int[] nums, int pos) {
        //进入这个函数就可以将path中的结果添加进ret中，这样就可以将空集的情况给考虑上
        ret.add(new ArrayList<>(path));
        //循环的话，就从pos位置开始遍历
        for (int i = pos; i < nums.length; i++) {
            path.add(nums[i]);
            dfs(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

在这里插入图片描述

3. 找出所有子集的异或总和再求和

https://leetcode.cn/problems/sum-of-all-subset-xor-totals/

3.1 题目要求

一个数组的异或总和定义为数组中所有元素按位 XOR 的结果；如果数组为空，则异或总和为 0 。

例如，数组 [2,5,6] 的异或总和为 2 XOR 5 XOR 6 = 1 。
给你一个数组 nums ，请你求出 nums 中每个子集的异或总和，计算并返回这些值相加之和。

注意：在本题中，元素相同的不同子集应多次计数。

数组 a 是数组 b 的一个子集的前提条件是：从 b 删除几个（也可能不删除）元素能够得到 a 。

示例 1：

输入：nums = [1,3]
输出：6
解释：[1,3] 共有 4 个子集：
- 空子集的异或总和是 0 。
- [1] 的异或总和为 1 。
- [3] 的异或总和为 3 。
- [1,3] 的异或总和为 1 XOR 3 = 2 。
0 + 1 + 3 + 2 = 6

示例 2：

输入：nums = [5,1,6]
输出：28
解释：[5,1,6] 共有 8 个子集：
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

示例 3：

输入：nums = [3,4,5,6,7,8]
输出：480
解释：每个子集的全部异或总和值之和为 480 。

提示：

1 <= nums.length <= 12
1 <= nums[i] <= 20

class Solution {
    public int subsetXORSum(int[] nums) {

    }
}

3.2 做题思路

这道题目跟上面的子集思路基本上没什么区别，之不过上面的子集是要求出所有子集的情况，而这道题目是求出所有子集异或之后的总和。因为思路基本跟上个题一样，所以我们直接来看代码。

3.3 代码实现

class Solution {
    int path;
    int ret;
    public int subsetXORSum(int[] nums) {
        dfs(nums, 0);
        return ret;
    }

    private void dfs(int[] nums, int pos) {
        //前面是将集合添加进ret中，这里我们是将每种情况加进ret中
        ret += path;
        for (int i = pos; i < nums.length; i++) {
            //这里我们不是将新加入的元素加入到path集合中，而是将新加入的元素和之前path元素的异或的结果异或
            path ^= nums[i];
            dfs(nums, i + 1);
            //恢复现场（两个相同的元素异或，结果为0）
            path ^= nums[i];
        }
    }
}

在这里插入图片描述

4. 全排列II

https://leetcode.cn/problems/permutations-ii/

4.1 题目要求

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {

    }
}

4.2 做题思路

这道题目跟全排列I 是不一样的，全排列I 中不存在重复的元素，但是这道题目中存在重复的元素，也就是说[1, 1, 2] 和 [1, 1, 2] 是同一个排列，这不看起来就是同一个排列吗？难道还能不同吗？其实这里的 1 不是同一个1，[1(下标为0), 1(下标为1), 2]，[1(下标为1), 1(下标为0), 2]，全排列I 中我们只需要使用一个标记数组来避免同一个元素被重复使用的情况，而这个全排列II 中，我们还需要筛选出因元素相同而导致的相同排列的情况。那么如何筛选呢？我们来看个例子：

在这里插入图片描述

4.3 代码实现

class Solution {
    List<Integer> path;
    List<List<Integer>> ret;
    boolean[] vis;
    public List<List<Integer>> permuteUnique(int[] nums) {
        path = new ArrayList<>();
        ret = new ArrayList<>();
        vis = new boolean[nums.length];
        //首先将重复元素给排序到一起
        Arrays.sort(nums);
        dfs(nums);
        return ret;
    }

    private void dfs(int[] nums) {
        if (path.size() == nums.length) {
            ret.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (vis[i] == false && (i == 0 || (nums[i - 1] != nums[i]) || vis[i - 1] == true)) {
                path.add(nums[i]);
                vis[i] = true;
                dfs(nums);
                //恢复现场
                path.remove(path.size() - 1);
                vis[i] = false;
            }
        }
    }
}