🏖️作者：@malloc不出对象
⛺专栏：《初识C语言》
👦个人简介：一名双非本科院校大二在读的科班编程菜鸟，努力编程只为赶上各位大佬的步伐🙈🙈

---

前言

本文要给大家带来的是时间复杂度与空间复杂度的讲解，这部分是我们学习数据结构与算法当中非常重要的一部分，判断一个算法的优劣主要就是这两部分决定的，所以要想写出一个好的算法程序了解这两部分是必不可少的。

一、算法效率

1.1 如何衡量一个算法的好坏

如何衡量一个算法的好坏呢？比如对于以下斐波那契数列：

long long Fib(int N)
{
	if(N < 3)
		return 1;
	return Fib(N-1) + Fib(N-2);
}

斐波那契数列的递归实现方式非常简洁，但简洁一定好吗？那该如何衡量其好与坏呢？

1.2 算法的复杂度

算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。 在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎，但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度，所以我们如今其实已经不需要再特别关注一个算法的空间复杂度，我们最看重的是它的时间效率。

二、时间复杂度

2.1 时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数(此函数为数学中的函数)，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

即：找到某条基本语句与问题规模N之间的数学表达式，就是算出了该算法的时间复杂度。

下面我们来简单的看下一个例子：

// 请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N ; ++ i)
	{
		for (int j = 0; j < N ; ++ j)
		{
			++count;
		}
	}
	
	for (int k = 0; k < 2 * N ; ++ k)
	{
		++count;
	}
	
	int M = 10;
	while (M--)
	{
		++count;
	}
	
	printf("%d\n", count);
}

此时count的执行次数可以简单的用一个数学表达式来表示：F(N) = N² + 2 * N + 10，这其实就是精确的时间复杂度：算法中基本操作的执行次数。

N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用大O的渐进表示法。

2.2 大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后，Func1的时间复杂度就为O(N²）了。

N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。举个简单的例子：今天王者出了一款皮肤，但是销售量并不高，而且还因此亏了点钱(手动dog~)，你觉得这笔钱对于腾哥来说他会放在心上吗？腾哥微微一笑格局小了，这点钱对于他来说就是三瓜俩枣，根本不会影响他的小金库，对他有影响的单位要以亿来衡量了，这也就是我们所说的保留影响大的项就可以了，其余对结果影响不大的项就可以省略了。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数(下界)

例如：在一个长度为N数组中搜索一个数据x
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到

那么在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)。
为什么总是要以最坏情况来进行衡量呢？这也是我们常听说的预期管理，例如：你跟你的女朋友如花约好一个时间点见面，本来你那天一下午其实没什么事要干，下午4点就可以约好了时间见面的，但是你故意延后到了6点，因为这段时间刚好也是在正常上班时间你怕会有人找你有事啥的，所以你为了保险一点把时间延后到了6点，然后在6点之前在女朋友的楼下拿着一束花等着她，蛙趣~这么蟀的男朋友谁不爱啊，如花下楼看见你心里直说这辈子我非你不嫁了🙈🙈(年度动画片来了，看就看了各位别当真哈哈哈~)；这样往往会产生意想不到的惊喜结果，而你约好的4点如果此时别人找你有事的话，此时如花心里又当如何作想呢(逃~)。所以说我们说话总是也要给自己留有余地的，有句话叫做话不能说的太满也同样的是这个道理。

2.3 常见时间复杂度计算举例

实例1：

void Func3(int N, int M)
{
	int count = 0;
	for (int k = 0; k < M; ++k)
	{
		++count;
	}
	for (int k = 0; k < N; ++k)
	{
		++count;
	}
	
	printf("%d\n", count);
}

这个案例应该是非常简单的，我们的算法基本执行次数为F(N) = M + N，用大O渐进法就表示为O(M + N)了，注意这里由于M与N都是未知数，所以不能省略项数。

实例2：

void Func4(int N)
{
	int count = 0;
	for (int k = 0; k < 100; ++k)
	{
		++count;
	}
	printf("%d\n", count);
}

这个算法的计算次数为F(N) = 100，它是一个常数所以用大O渐进法表示为O(1)，为什么说100次也可以被当中一个常数来看待呢？这是由于CPU的执行速度非常快，100次几乎不需要花费时间就能完成，所以它可以被当做常数项1看待。

下面我们来做一个简单的对比：

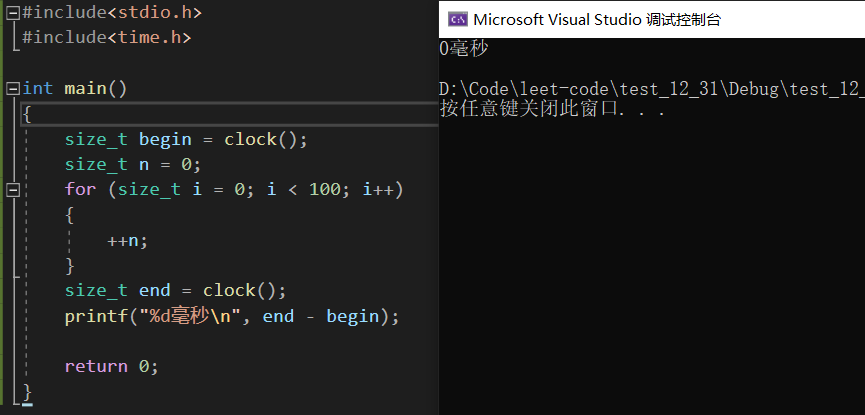
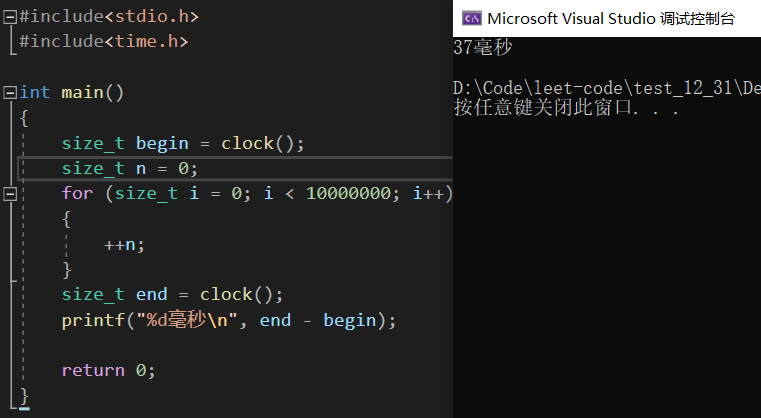
通过这俩张图我们可以发现100与10^8次数计算时间甚至相差无几，此时的i应该是编译器进行了一定的优化，将原本需要从内存中一个个进行读取优化到寄存器中进行读取，这样的计算速度非常之快，所以我们看到100跟千万级别的数都是一瞬间完成的，都可以把它们当做常数项来看待。这样也许有人会问了我们平常的N基本都是在10^9范围内的，你要这样说的话，那O(N)不也可以当做O(1)吗？其实O(1)与O(N)根本不是一个量级的，N是一个未知数，而我们1只是一个确定的常量数，而且其实我们平常见到的常数级其实也达不到10^8，大多都是成百上千上万的这样，这里我们一定要从量级上将它们区分开来看。

实例3：

void Bubble_sort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		for (int j = 0; j < n - i - 1; j++)
		{
			if (...)
			{
				...
			}
		}
	}
}

关于冒泡排序想必大家都会，它的核心思想是每次进行俩俩交换确定一个最大或最小的数，最后进行n - 1次比较此时就呈一个有序的状态了。下面我们来计算一下冒泡排序的时间复杂度：F(N) = n - 1 + n - 2 + …+ 2 + 1，此时它其实呈的是一个等差数列公差为1，F(N) = (n - 1 + 1) * (n - 1) / 2；首项加尾项乘以项数除以2，此时用大O渐进法就表示成了O(N²)。

实例4：

int BinarySearch(int* a, int n, int target)
{
	int l = 0;
	int r = n - 1;
	
	while (l <= r)
	{
		int mid = l + ((r - l) >> 1);
		if (a[mid] < target)
			l = mid + 1;
		else if (a[mid] > target)
			r = mid - 1;
		else
			return mid;
	}
	return -1;
}

这是一段标准的二分查找模板，二分思想也非常的简单，每次进行折半查找直到遇到target否则返回最接近target元素的那个位置(这里返回的是-1)，那么它的时间复杂度为O(logN)想必大家也都清楚，那么它是如何计算得来的呢？下面就带大家简单的算一下。

每次查找查找区间缩小一半，查找多少次呢？就是求除2多少次？
N / 2 / 2 …/ 2 = 1，假设查找x次， N = 1 *2 *2 …* 2，N = 2 ^ x， x = logN，这里的底数2我们此时忽略了，其他的底数不能忽略，我们一般的其实也很少见其他的底数，所以最终的时间复杂度就为O(logN)了。

实例5：

long long Fac(size_t N)
{
	if (1 == N)
		return 1;
	return Fac(N - 1) * N;
}

这是一段很简单的求N阶乘的代码，它的时间复杂度又为什么呢？我们该如何去计算呢？

首先我们来看看递归，调用自身的函数的可以简单的称做递归了，这段函数它要进行调用N次，而每次调用函数执行的是常数次，所以最终计算次数相加就为N次了，时间复杂度就为O(N)。我们再通过一张图来理解一下这个过程：

这里再说明一下，我们怎么来判断执行次数呢？像这段代码我们没有一个统一的标准，if执行算不算，return算不算…，虽然算进来都是常量级不影响最后的结果，但是这样未免有些烦琐了，，所以干脆我们看到循环条件了就判别它的执行次数，其余的条件啥的一律按照常数量来算就把它们当做执行次数为1.

实例6：

long long Fib(size_t N)
{
	if (N < 3)
		return 1;
	return Fib(N - 1) + Fib(N - 2);
}

这段代码依旧很熟悉，它就是我们常用的斐波那契数列，想必对于一个科班的学生来说都见过，它的代码这么的简洁，那它的时间复杂度也会很小吗？为什么我们大多数情况其实不用递归而用其改进的迭代法代替呢？下面我们来一探究竟。

关于递归我最想说的一点是多去画图分析，画图出来很多问题分析起来就非常的清晰了，，因为其实递归相对来说是非常简洁的，但其中蕴含的奥妙实在是妙不可言，，递归对于我来说是一直是一个非常头疼的问题，我也是秉持着能不用递归坚决不用递归的原则哈哈~，因为博主水平太有限了，废话不多说我们回到正题，同时也是通过一张图让大家了解一下这个过程：

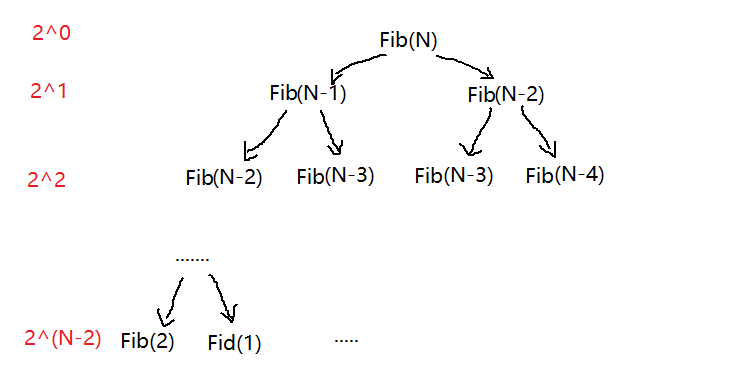
F(N) = 2 ^ 0 + 2 ^ 1 + 2 ^ 2 + …+ 2 ^ (n - 3) + 2 ^ (n - 2) ==> O(2 ^ N)，它的次数相加起来呈一个等比数列，根据等比数列公示就能表示出时间复杂度了，最后再提一点实际上最后一项是达不到2 ^ (n - 2)次的，因为右边部分项必定要先比左边调用到Fib(2)和Fib(1)也就是最后一层，所以最后一层实际上是有缺失的，如下图：

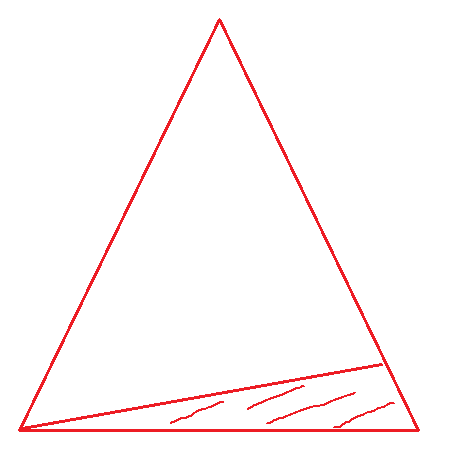
最终我们得到斐波那契数列递归调用的时间复杂度是O(2^N)，它是呈爆炸式增长的，N越大增长越恐怖，它比O(N²)还要慢上不少！！！这就是为什么大多数情况下求斐波那契数列不使用递归的原因，一旦N稍微大一点直接卡在那个地方等很久才出结果要么是程序直接发生崩溃，而用迭代法替代时间复杂就变为了O(N)，所以很快就能求出斐波那契数列的结果，即使N很大也能立马得到结果，但结果的正确性就不知道了，因为N一旦过大计算得出的结果可能会溢出等…

最后总结一下函数递归调用如何计算时间复杂度：首先函数调用是不会影响时间复杂度的，影响时间复杂度的是函数内部程序的执行次数，将每次函数调用内部程序的执行次数相加起来得到的就是总的执行次数，由此就可以推断出时间复杂度了。

三.空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。 空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。

空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。

注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

实例1：

int BinarySearch(int* a, int n, int target)
{
	int l = 0;
	int r = n - 1;
	
	while (l <= r)
	{
		int mid = l + ((r - l) >> 1);
		if (a[mid] < target)
			l = mid + 1;
		else if (a[mid] > target)
			r = mid - 1;
		else
			return mid;
	}
	return -1;
}

我们来看看二分查找模板的空间复杂度，它定义了三个变量l、r以及mid，所以它的量级为常数级，最终空间复杂度就为O(1)了，关于空间复杂度其实很简单就看它显式定义了几个变量就可以了。

实例2：

void Fac(int* nums, int n)
{
	int* a = (int*)malloc(n + 1);

	....
}

这段伪代码的空间复杂就为O(N)了，它显示动态的开辟了n+1个空间。

实例3：

long long Fac(size_t N)
{
	if (1 == N)
		return 1;
	return Fac(N - 1) * N;
}

看向这段函数递归调用的代码，我们没有发现它显式申请什么额外的空间啊，那么它的空间复杂度为O(1)? 跟计算函数递归调用的时间复杂度一样我们计算的是每次函数调用内部程序额外开辟的空间次数，我们通过画图分析一下：

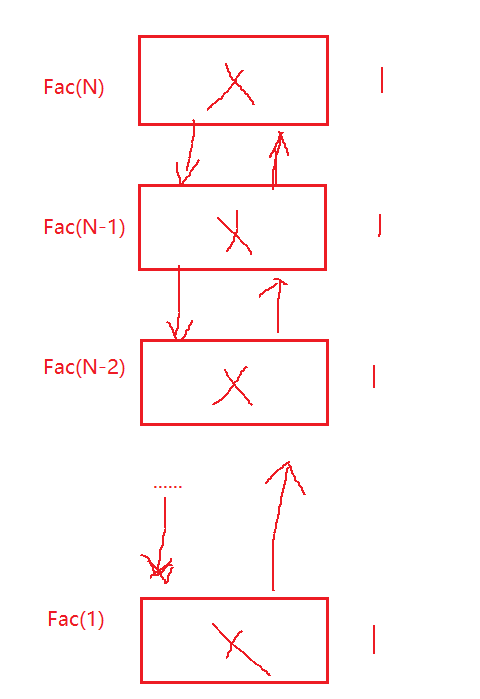
大家知道函数调用时会创建一块函数栈帧，此时每次函数调用都会在其函数栈帧内部开辟常数量的变量(跟我们计算时间复杂度执行次数时采取的是一样的规则)，所以将每次函数调用开辟的空间加起来最终就是整个程序额外申请的空间，此时空间复杂为O(N).

实例四：

long long Fib(size_t N)
{
	if (N < 3)
		return 1;
	return Fib(N - 1) + Fib(N - 2);
}

同样的对于计算函数递归调用的时空复杂度我们采用画图的形式来展现，在讲这个问题之前我们问大家一个问题在第一次return Fib(N-1) + Fib(N-2)时，是先去调用Fib(N-1)再去调用Fib(N-2)吗？？这个问题非常巨迷惑性，包括之前的我也是一直认为是先调用Fib(N-1)再去调用Fib(N-2)再继续层层调用下去的，，我之前一直想的是这样的调用顺序：

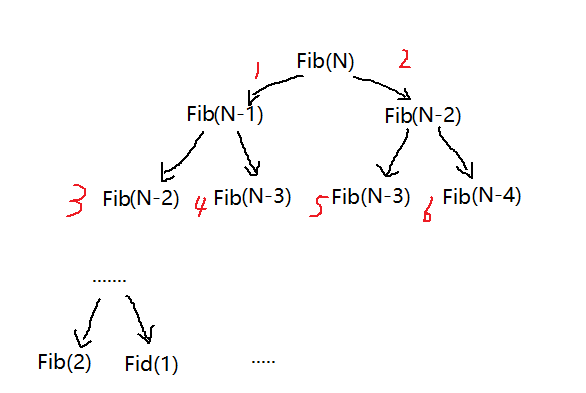
但其实是这样来进行调用的，它会根据一条路直接走到底然后再返回走另外一条路来回进行穿插，，这个例子用二叉树的前序遍历来理解再好不过了，先由根节点递归左子树再右子树，，把左子树全部走完了再来走右子树这样一条路走到尽头再走另外一条路，，下面通过图形来展示一下这个递归调用的执行过程：

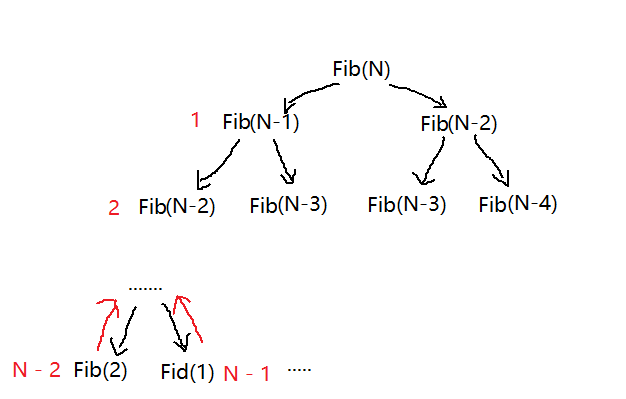
大家知道所谓递归其实是分为两个部分的，一个部分是递：层层递进出口条件；一个部分是归：回到上一次函数调用结束的位置继续执行函数内部未执行完的代码。

正如上面一张图那样，我们一直递归到Fib(2)这是最后一层了，所以我们要返回上一次函数调用结束的地方执行未执行完的代码，Fib(2)上一次的函数是Fib(3)，它return Fib(2) + Fib(1)；那么Fib(2)我们已经返回了答案，接着执行未执行的代码于是就调用Fib(1)，Fib(1)也是最后一层所以直接返回到Fib(3)，那么Fib(3)内部此时的代码已经执行完毕，此时又该返回上一层Fib(4)函数执行未执行完的代码，，如此便是递归的整个过程，，还有一个地方需要注意函数调用结束之后，函数栈帧也随之销毁，，但我们要注意一句话销毁并不代码这块空间没了，，它同样的还是存在，，只不过是我们不能利用这块空间原来的内容罢了。接下来还是给大家拓展一下这部分的内容。

3.1 计算机中所谓的删除数据究竟是在做什么

在我们的日常生活中常常遇到这种问题，我们下载一部高清电影几个g的那种一般来说需要几分钟的甚至更长的时间，在删除时我们只需几秒钟就完成了，理论上来讲你觉得合理嘛，我觉得非常的不合理，那么我们的计算机究竟进行了何等操作才让删除数据时变得如此之快呢？还有所谓的删除数据是真的将这些数据全部彻底清空了吗？下面我们一起来谈谈这个问题。

我们将几个g的高清电影先缓存到硬盘，之后在将数据加载到内存当中，由CPU等进行读取数据，我们的计算机只认识二进制，所以读取的数据全部为二进制数据，换而言之计算机读取的数据全是0/1数据，那么计算机在释放空间时是否是将我们的数据全部清0/1呢？答案并不是，在对我们的数据进行清0/1的时候，计算机也需对数据进行写入操作，换而言之我们下载几个g的内容就要对这几个g的内容进行写入操作，所以如果是这种方式对我们的数据进行删除的话需要的时间也跟下载时的消耗的时间相差无几。

那么计算机到底是如何进行”删除“清空数据的呢？

本质上计算机清空数据，只要通过某种方式设置该数据无效即可。假设这几个g有几个代码块，我们将这几个代码块设置成几个bit位，在计算机进行清空数据时我们只需将对应的代码块(bit位)进行清0操作即可，表示该代码块的数据已经无效，后续加载进来的数据可以继续在这块代码块上进行写入覆盖这块代码块。这样做有几个好处：1.实际上只是真正意义上删除了少量数据 2.不用高频的对磁盘这个存储介质或者其他任何存储介质进行充放电或者读写可以有效的增长我们硬件的寿命。

这里我们还可以举个栗子：在电视剧当中我们经常看到某某某被抄家了，之后那些小嘎鲁兵就在门上贴上一个大大的拆字表示一段时间内该房子不能住人了，而并不是将该房子拆了，后续假如有人买了这套房子就可以对这房子进行改装等各种操作了。

好了，接下来我们继续看一个例子证明一下：

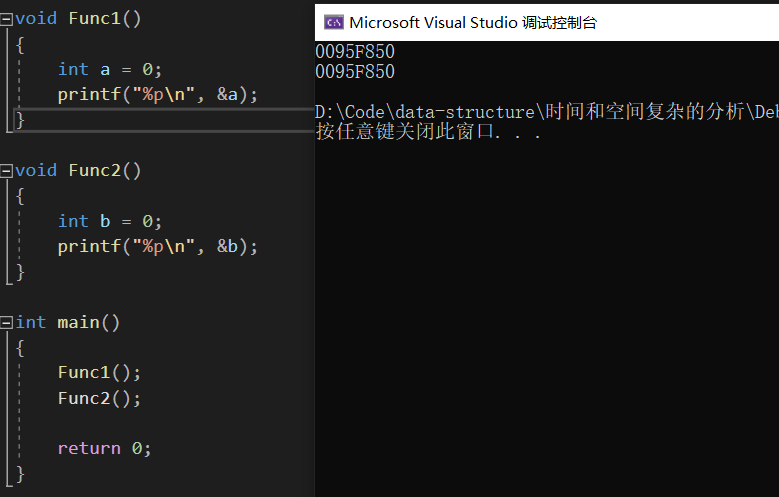
我们发现什么？两个不同的函数内变量的地址是一样的？这是巧合吗？
不是的，读者也可以自行进行反复验证，这是因为Func1()函数在调用完毕之后，它的函数栈帧空间被销毁了，，而调用Func2()函数编译器提前根据它内部定义的变量开辟一个合适大小的栈帧空间，，此时Func2()函数就直接覆盖了原先被销毁的Func1()函数的栈帧空间，并且在相同的位置为变量开辟一块空间，，这样也就达到了重复利用空间资源的目的，，不然的话如果一个函数调用结束之后它的栈帧空间被销毁就不能被使用了，，这样带来极大的空间资源浪费。

回到计算上述代码空间复杂的问题，，讲上面的一切只是为了做此处的铺垫，下面我就来计算一下空间复杂度，，我们通过下图来进行展示：

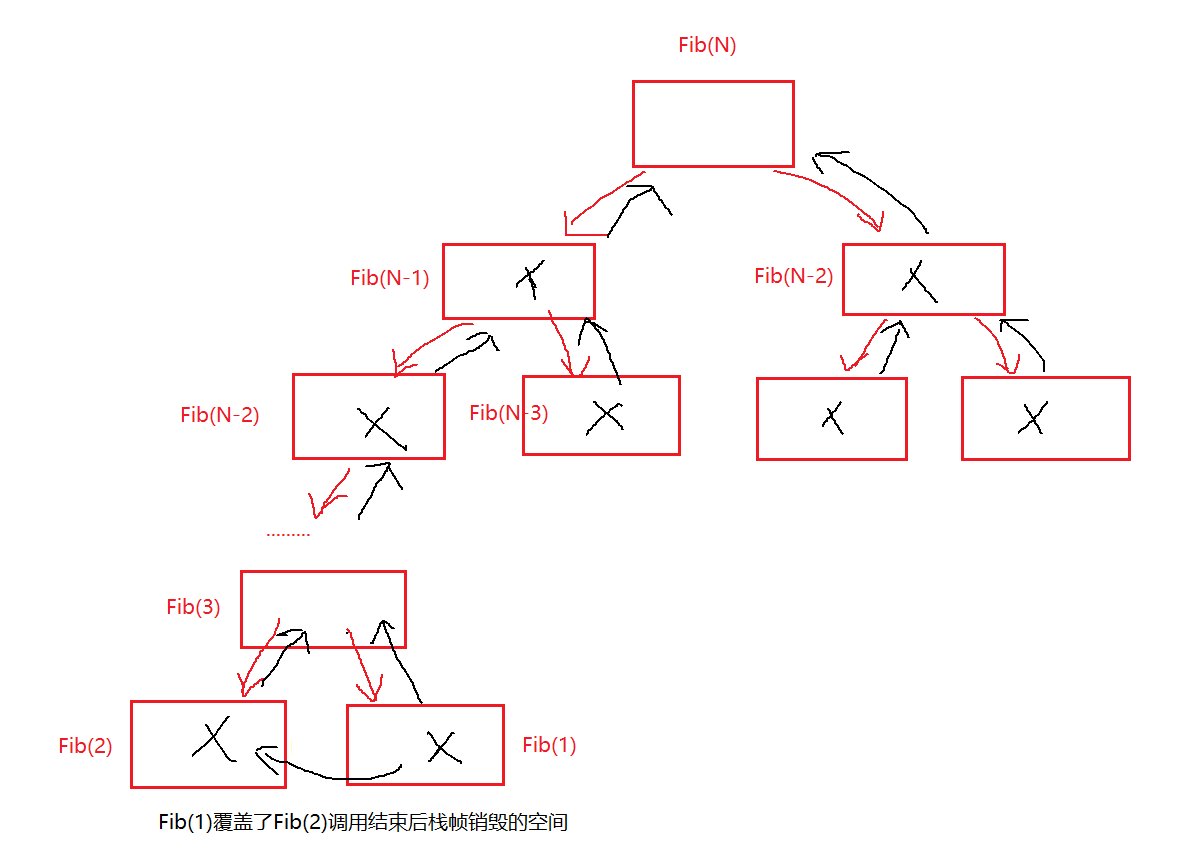
以上代码的关键点是：时间是一去不复返的，但空间是可以重复利用的。

我们开辟了N - 2个空间，，它们调用结束的空间之后都是可以进行相互覆盖重复利用的，，所以最终该代码的空间复杂为O(N).

四、常见复杂度对比

一般算法常见的复杂度如下:

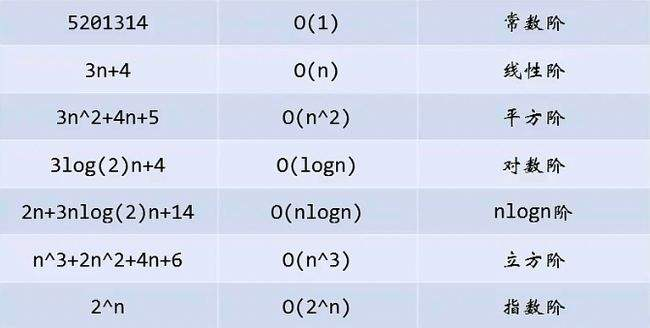
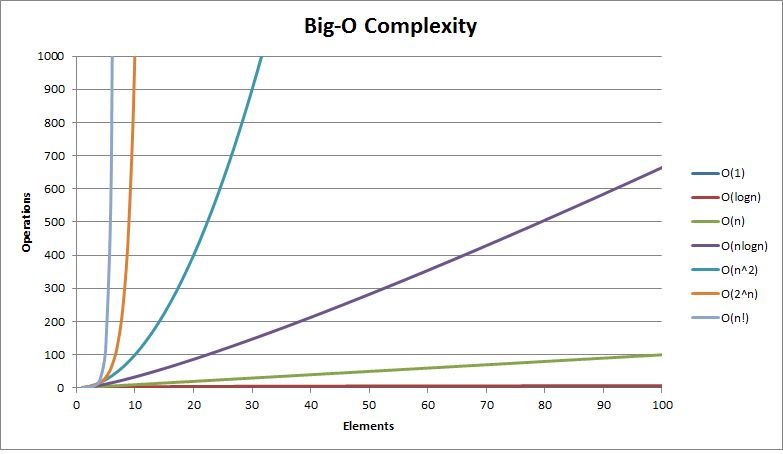
关于时间与空间复杂的讲解就到这儿了，，如有疑问或是错处可以评论区互相交流哈，，，写完这篇文章此时又是新的一年了，，祝所有的小伙伴们新年快乐啊😋😋在学习的同时也要好好注意自己的身体哦，，新的一年一起加油一起进步，，与大家共勉！！