在深度学习中，丢弃法（Dropout）是一种常用的正则化技术，旨在减少模型的过拟合现象，可能会比之前的权重衰减(Weight Decay)效果更好。通过在训练过程中随机丢弃一部分神经元，可以有效地减少神经网络中的参数依赖性，增强模型的泛化能力。

一、丢弃法原理介绍

1、动机

       一个好的模型需要对输入数据的扰动鲁棒，也就是说，不管图片加入多少噪音，我也是能看清楚的。使用有噪音的数据等价于Tikhonov正则，正则使得权重值范围不会太大，避免一定的过拟合。与之前加入的噪音不一样，之前是固定噪音，丢弃法是随机噪音，丢弃法不是在输入加噪音，而是在层之间加入噪音，所以丢弃法也算是一个正则。

2、无偏差的加入噪音

       假如是上一层到下一层的某一个输出（上一层输出向量的某一个元素）的话，对加入噪音得到，我们希望加入噪音后不改变期望，即：

       丢弃法对上一层输出向量的每一个元素做如下扰动：

       此时这个元素的期望是不变的：

3、丢弃法的使用

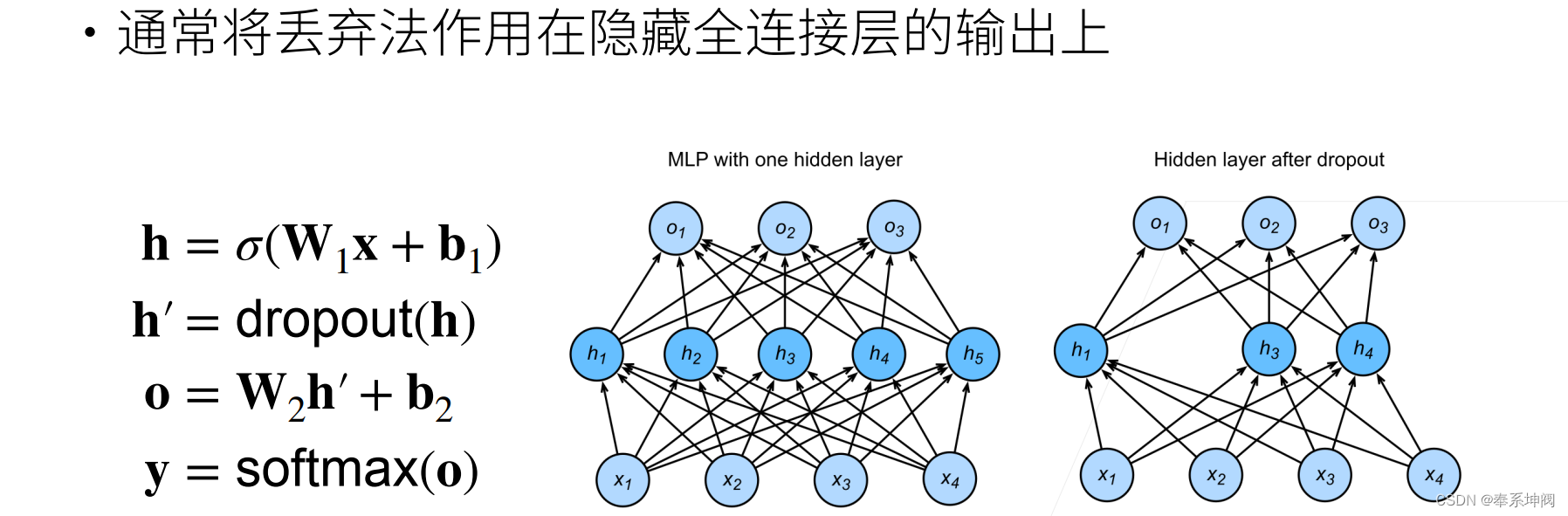
       通常将丢弃法作用在隐藏全连接层的输出上。如图"MLP with one hidden layer"带有1个隐藏层和5个隐藏单元的多层感知机。当我们将暂退法应用到隐藏层，以的概率将隐藏单元置为零时，结果可以看作一个只包含原始神经元子集的网络。比如在图"Hidden layer after dropout"中，删除了和，因此输出的计算不再依赖于或，并且它们各自的梯度在执行反向传播时也会消失。这样，输出层的计算不能过度依赖于的任何一个元素。

4、推理中的丢弃法

5、总结

• 丢弃法将一些输出项随机置0来控制模型复杂度
• 常作用在多层感知机的隐藏层输出上
• 丢弃概率是控制模型复杂度的超参数

二、暂退法从零开始实现

1、定义dropout函数

       要实现单层的暂退法函数，我们从均匀分布中抽取样本，样本数与这层神经网络的维度一致。然后我们保留那些对应样本大于的节点，把剩下的丢弃。

       在下面的代码中，我们实现 `dropout_layer` 函数，该函数以`dropout`的概率丢弃张量输入`X`中的元素，如上所述重新缩放剩余部分：将剩余部分除以`1.0-dropout`。

import torch
from torch import nn
from d2l import torch as d2l

def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    # torch.rand(X.shape)生成了一个与输入张量X相同形状的随机数张量，其中的元素值在[0, 1)的区间内均匀分布。
    # (torch.rand(X.shape) > dropout)执行了一个逻辑判断，将随机数张量中大于dropout的元素置为True，小于等于dropout的元素置为False。
    # .float()将布尔型张量转换为浮点型张量，将True转换为1.0，将False转换为0.0。
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

       我们可以通过下面几个例子来测试`dropout_layer`函数。我们将输入`X`通过暂退法操作，暂退概率分别为0、0.5和1。

X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))

tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  2.,  0.,  6.,  0.,  0.,  0., 14.],
        [16., 18.,  0., 22.,  0., 26., 28., 30.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

2、定义模型参数

       同样，我们使用Softmax回归中引入的Fashion-MNIST数据集（不懂的可以看链接里面的文章）。我们定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元。

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

3、定义模型

       我们可以将暂退法应用于每个隐藏层的输出（在激活函数之后），并且可以为每一层分别设置暂退概率：常见的技巧是在靠近输入层的地方设置较低的暂退概率。下面的模型将第一个和第二个隐藏层的暂退概率分别设置为0.2和0.5，并且暂退法只在训练期间有效。

dropout1, dropout2 = 0.2, 0.5    # 在靠近输入层的地方设置较低的暂退概率，因此dropout1设为0.2

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out


net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

4、训练和测试

       这类似于前面描述的多层感知机训练和测试。

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)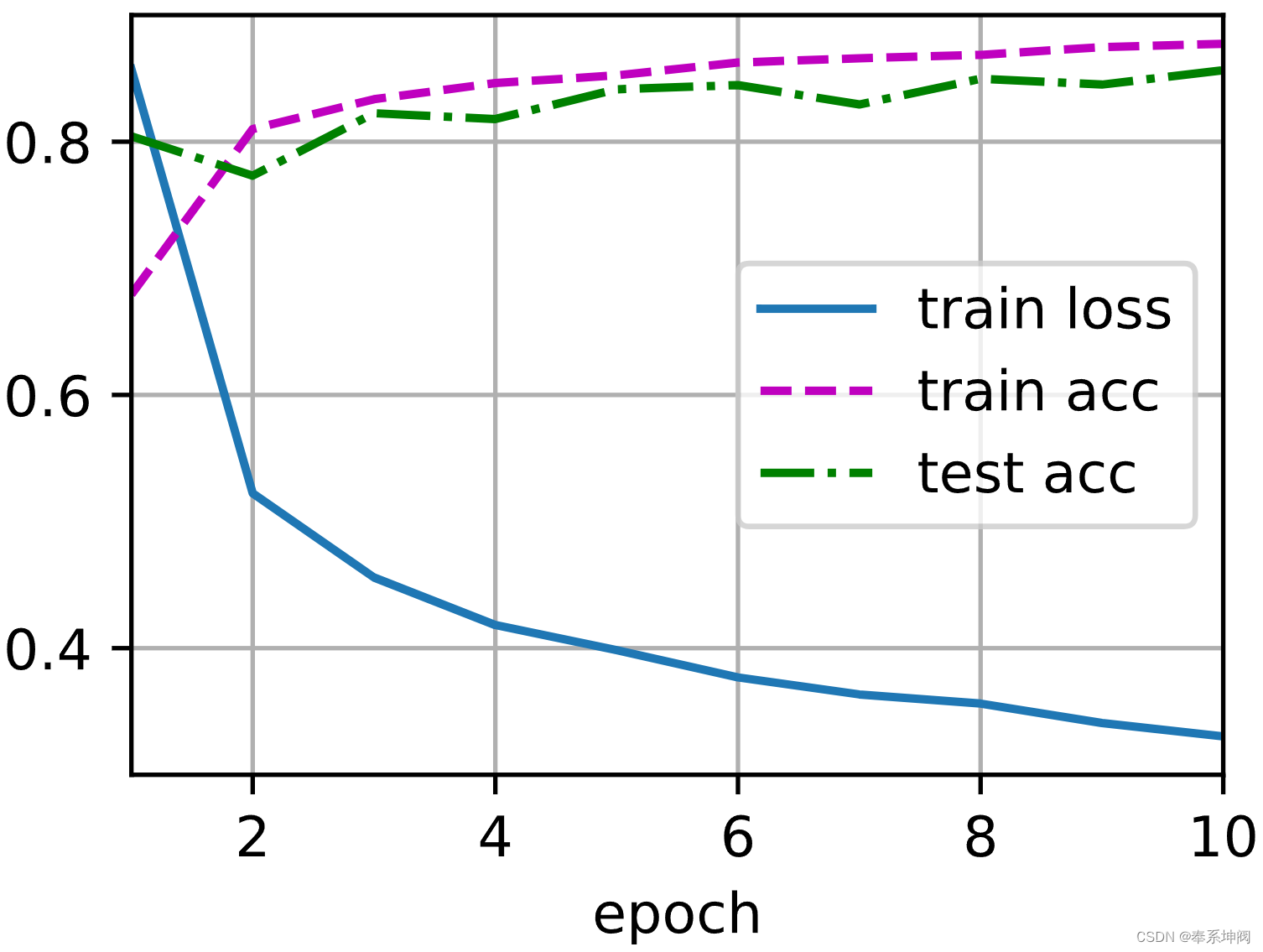

三、暂退法简洁实现

1、定义模型

       对于深度学习框架的高级API，我们只需在每个全连接层之后添加一个`Dropout`层，将暂退概率作为唯一的参数传递给它的构造函数。在训练时，`Dropout`层将根据指定的暂退概率随机丢弃上一层的输出（相当于下一层的输入）。在测试时，`Dropout`层仅传递数据。

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

2、训练和测试

       接下来，我们对模型进行训练和测试。

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

四、总结

• 暂退法在前向传播过程中，计算每一内部层的同时丢弃一些神经元。
• 暂退法可以避免过拟合，它通常与控制权重向量的维数和大小结合使用的。
• 暂退法将活性值替换为具有期望值的随机变量。
• 暂退法仅在训练期间使用。