《点云处理》平面拟合

news2024/11/24 4:40:49

前言

在众多点云处理算法中，其中关于平面拟合的算法十分广泛。本篇内容主要是希望总结归纳各类点云平面拟合算法，并且将代码进行梳理保存。

环境：

VS2019 + PCL1.11.1

1.RANSAC

使用ransac对平面进行拟合是非常常见的用法，PCL库中就有RANSAC拟合平面的实现代码，而且还集成了 两种拟合平面的代码。
方法一：

/// <summary>
/// 使用PCL中集成的RANSAC方法进行平面拟合
/// </summary>
/// <param name="cloud_in">输入待拟合的点云</param>
/// <param name="inliers">RANSAC拟合得到的内点</param>
/// <param name="coefficients">得到的平面方程参数</param>
/// <param name="iterations">平面拟合最大迭代次数</param>
/// <param name="threshold">RANSAC拟合算法距离阈值</param>
void RANSAC(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud_in, std::vector<int>& inliers, Eigen::VectorXf& coefficients,
    const int& iterations, const double& threshold)
{
    inliers.clear();                                          // 用于存放内点索引的vector
    pcl::shared_ptr<pcl::SampleConsensusModelPlane<pcl::PointXYZ>> model(new pcl::SampleConsensusModelPlane<pcl::PointXYZ>(cloud_in)); //定义待拟合平面的model，并使用待拟合点云初始化
    pcl::RandomSampleConsensus<pcl::PointXYZ> ransac(model);  // 定义RANSAC算法模型
    ransac.setDistanceThreshold(threshold);                   // 设定阈值
    ransac.setMaxIterations(iterations);                      // 设置最大迭代次数
    ransac.setNumberOfThreads(10);                            // 设置线程数量
    ransac.computeModel();                                    // 拟合 
    ransac.getInliers(inliers);                               // 获取内点索引
    Eigen::VectorXf params;                                   // 第一次得到的平面方程
    ransac.getModelCoefficients(params);                      // 获取拟合平面参数，对于平面ax+by_cz_d=0，params分别按顺序保存a,b,c,d
    model->optimizeModelCoefficients(inliers, params, coefficients);      // 优化平面方程参数
    std::vector<double> vDistance;                            // 用于存储每个点到拟合平面的距离的vector容器
    model->getDistancesToModel(coefficients, vDistance);      // 得到每个点到平面的距离的集合
    std::cout << "params: " << params[0] << ", " << params[1] << ", " << params[2] << ", " << params[3] << std::endl;
    std::cout << "coefficients: " << coefficients[0] << ", " << coefficients[1] << ", " << coefficients[2] << ", " << coefficients[3] << std::endl;
}

上述代码需要注意的是，一定需要model->optimizeModelCoefficients(inliers, params, coefficients); 通过这一句代码去优化平面参数。优化前后差别很大，如下图所示：
在这里插入图片描述
方法二：

/// <summary>
/// 使用PCL中集成的用于点云分割的RANSAC方法进行平面拟合
/// </summary>
/// <param name="cloud_in">输入待拟合的点云</param>
/// <param name="inliers">RANSAC拟合得到的内点</param>
/// <param name="coefficients">得到的平面方程参数</param>
/// <param name="iterations">平面拟合最大迭代次数</param>
/// <param name="threshold">RANSAC拟合算法距离阈值</param>
void SEG_RANSAC(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud_in, pcl::PointIndices::Ptr& inliers, Eigen::VectorXf& coefficients,
    const int& iterations, const double& threshold)
{
    if (inliers == nullptr) inliers.reset(new pcl::PointIndices);
    pcl::ModelCoefficients::Ptr coefficients_m(new pcl::ModelCoefficients);
    pcl::SACSegmentation<pcl::PointXYZ> seg;
    seg.setOptimizeCoefficients(true);
    seg.setModelType(pcl::SACMODEL_PLANE);
    seg.setMethodType(pcl::SAC_RANSAC);
    seg.setMaxIterations(iterations);                     // 设置最大迭代次数
    seg.setDistanceThreshold(threshold);                  // 设定阈值
    seg.setNumberOfThreads(10);                           // 设置线程数量
    seg.setInputCloud(cloud_in);
    seg.segment(*inliers, *coefficients_m);

    coefficients.resize(4);
    coefficients[0] = coefficients_m->values[0]; coefficients[1] = coefficients_m->values[1];
    coefficients[2] = coefficients_m->values[2]; coefficients[3] = coefficients_m->values[3];
    std::cout << "SEG coefficients: " << coefficients[0] << ", " << coefficients[1] << ", " << coefficients[2] << ", " << coefficients[3] << std::endl;
}

方法二其实也提到了优化平面参数，seg.setOptimizeCoefficients(true);这句代码就是比较关键的，需要加上。
上述两种方法的运行结果如下，从结果和运行时间来看，两种方法几乎一致。
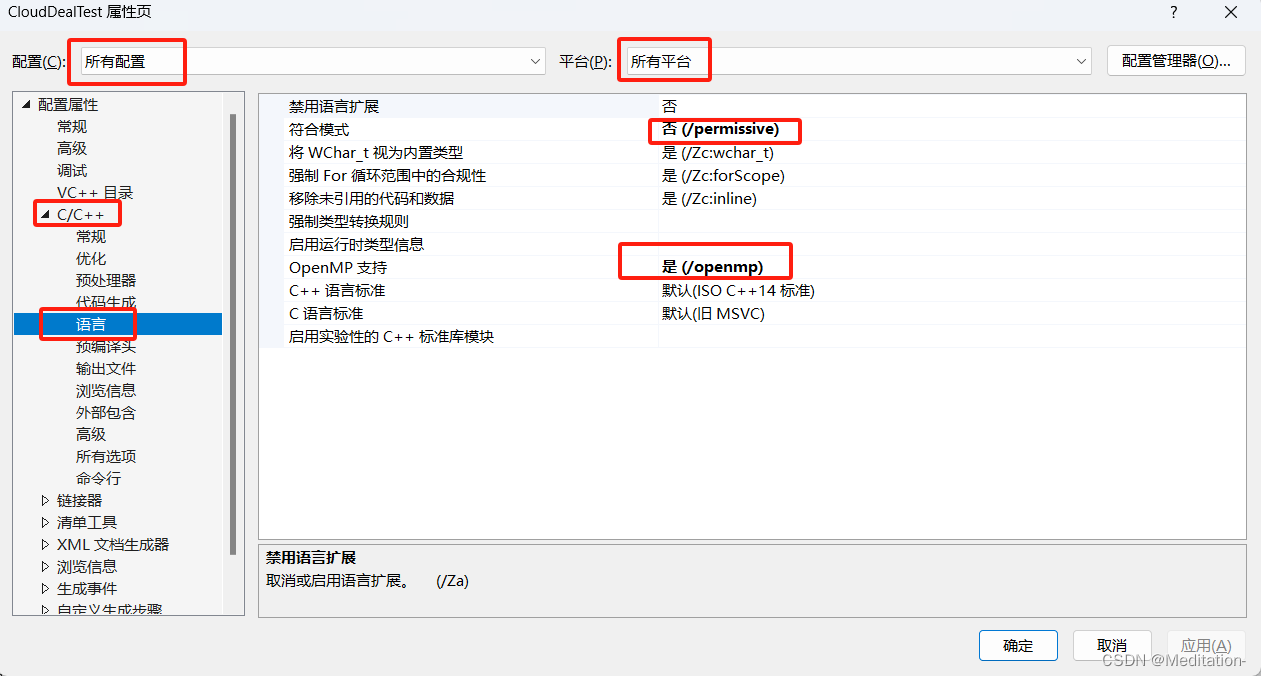
在这里插入图片描述
两种方法中都有一个设置线程的功能setNumberOfThreads(10); 但是这句话根本没有起到作用，下图中有提示[pcl::RandomSampleConsensus::computeModel] Parallelization is requested, but OpenMP 3.1 is not available! Continuing without parallelization.其实在VS中已经开启了openmp，也包含了头文件#include <omp.h>，只不过版本不对应，该问题也查阅了很久，没查到解决办法。

VS中开启openmp加速的配置方法：
在这里插入图片描述

2.最小二乘法拟合平面

除了RANSAC之外，另一种十分常见的拟合方程的方法是最小二乘法，这里就不过多介绍相关的理论知识，这里提到了相关的代码和原理

当然还是要贴上封装的C++代码实现：

/// <summary>
/// 使用最小二乘法拟合平面：Ax + By + Cz + D = 0 */   //拉格朗日乘子法 https://zhuanlan.zhihu.com/p/390294059
/// </summary>
/// <param name="xjData">输入待拟合平面的点云</param>
/// <param name="coefficients">输出拟合的平面方程</param>
/// <returns>输入点云点数符合要求，返回true，否则返回false</returns>
bool LeastSquare(const pcl::shared_ptr<pcl::PointCloud<pcl::PointXYZ>>& xjData, Eigen::VectorXf& coefficients)
{
    int count = xjData->points.size();
    if (count < 3) return false;

    double meanX = 0, meanY = 0, meanZ = 0;
    double meanXX = 0, meanYY = 0, meanZZ = 0;
    double meanXY = 0, meanXZ = 0, meanYZ = 0;
    for (int i = 0; i < count; i++)
    {
        meanX += xjData->points[i].x;
        meanY += xjData->points[i].y;
        meanZ += xjData->points[i].z,

        meanXX += xjData->points[i].x * xjData->points[i].x;
        meanYY += xjData->points[i].y * xjData->points[i].y;
        meanZZ += xjData->points[i].z * xjData->points[i].z;

        meanXY += xjData->points[i].x * xjData->points[i].y;
        meanXZ += xjData->points[i].x * xjData->points[i].z;
        meanYZ += xjData->points[i].y * xjData->points[i].z;
    }
    meanX /= count; meanY /= count; meanZ /= count;
    meanXX /= count; meanYY /= count; meanZZ /= count;
    meanXY /= count; meanXZ /= count; meanYZ /= count;

    /* eigenvector */
    Eigen::Matrix3d eMat;
    eMat(0, 0) = meanXX - meanX * meanX; eMat(0, 1) = meanXY - meanX * meanY; eMat(0, 2) = meanXZ - meanX * meanZ;
    eMat(1, 0) = meanXY - meanX * meanY; eMat(1, 1) = meanYY - meanY * meanY; eMat(1, 2) = meanYZ - meanY * meanZ;
    eMat(2, 0) = meanXZ - meanX * meanZ; eMat(2, 1) = meanYZ - meanY * meanZ; eMat(2, 2) = meanZZ - meanZ * meanZ;
    Eigen::EigenSolver<Eigen::Matrix3d> xjMat(eMat);           // 求取矩阵特征值和特征向量的函数EigenSolver
    Eigen::Matrix3d eValue = xjMat.pseudoEigenvalueMatrix();   // 获取矩阵伪特征值 3*3
    Eigen::Matrix3d eVector = xjMat.pseudoEigenvectors();      // 获取矩阵伪特征向量 3*1

    /* the eigenvector corresponding to the minimum eigenvalue */
    double v1 = eValue(0, 0); double v2 = eValue(1, 1); double v3 = eValue(2, 2);
    int minNumber = 0;
    if ((abs(v2) <= abs(v1)) && (abs(v2) <= abs(v3)))
    {
        minNumber = 1;
    }
    if ((abs(v3) <= abs(v1)) && (abs(v3) <= abs(v2)))
    {
        minNumber = 2;
    }
    double A = eVector(0, minNumber); double B = eVector(1, minNumber); double C = eVector(2, minNumber);
    double length = sqrt(A * A + B * B + C * C);
    A /= length; B /= length; C /= length;
    double D = -(A * meanX + B * meanY + C * meanZ);

    /* result */
    if (C < 0)
    {
        A *= -1.0; B *= -1.0; C *= -1.0; D *= -1.0;
    }

    coefficients.resize(4);
    coefficients[0] = A; coefficients[1] = B; coefficients[2] = C; coefficients[3] = D;

    std::cout << "LS coefficients: " << coefficients[0] << ", " << coefficients[1] << ", " << coefficients[2] << ", " << coefficients[3] << std::endl;
}

同一份点云，使用最小二乘法拟合结果如下：
在这里插入图片描述
最小二乘法拟合平面方程和上述RANSAC拟合结果还是有些差别的，但是RANSAC运行时间约为0.02s，而最小二乘法运行时间需要0.0013s，最小二乘法运行时间要比RANSAC快很多。如果针对一份没有太多噪点，很平滑干净的点云，可以使用最小二乘法去拟合，但是如果是有噪点的点云，追求准确率的情况下，则需要使用RANSAC进行拟合。

3.SVD分解的方法求平面方程

可以通过Eigen实现使用SVD分解的方法进行平面方程求解

/// <summary>
/// 通过SVD分解的方法求拟合平面
/// </summary>
/// <param name="pcl_cloud">输入待拟合平面点云</param>
/// <param name="coefficients">输出拟合平面的参数</param>
void PlaneEigenSVD(const pcl::PointCloud<pcl::PointXYZ>& pcl_cloud, Eigen::VectorXf& coefficients)
{
    if (pcl_cloud.points.size() < 3) return;
    // Convert PCL point cloud to Eigen matrix
    Eigen::Matrix<float, 3, Eigen::Dynamic> coord(3, pcl_cloud.size());
    for (size_t i = 0; i < pcl_cloud.size(); ++i)
    {
        coord.col(i) << pcl_cloud[i].x, pcl_cloud[i].y, pcl_cloud[i].z;
    }

    // Calculate centroid
    Eigen::Vector4f centroid;
    pcl::compute3DCentroid(pcl_cloud, centroid);

    // Subtract centroid
    coord.row(0).array() -= centroid(0);
    coord.row(1).array() -= centroid(1);
    coord.row(2).array() -= centroid(2);

    // Perform singular value decomposition (SVD)
    Eigen::JacobiSVD<Eigen::Matrix<float, Eigen::Dynamic, Eigen::Dynamic>> svd(coord, Eigen::ComputeThinU | Eigen::ComputeThinV);
    Eigen::Vector3f plane_normal = svd.matrixU().rightCols<1>();

    // Create PCL ModelCoefficients
    coefficients.resize(4);
    coefficients[0] = plane_normal(0);
    coefficients[1] = plane_normal(1);
    coefficients[2] = plane_normal(2);
    coefficients[3] = -(plane_normal(0) * centroid(0) + plane_normal(1) * centroid(1) + plane_normal(2) * centroid(2));
    if (coefficients[2] < 0) coefficients = -coefficients;

    std::cout << "SVD coefficients: " << coefficients[0] << ", " << coefficients[1] << ", " << coefficients[2] << ", " << coefficients[3] << std::endl;

    return;
}

运行结果如下：
在这里插入图片描述
得到的结果其实和最小二乘法拟合得到的结果一样，但是耗时更长一些。

4.霍夫变换进行平面拟合

其实使用霍夫变换去拟合几何模型也是一件非常常见的方法，但是目前没有相关代码进行测试验证，如果后续有找到实现方法也会更新在这里。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1317447.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

josef约瑟 时间继电器 DS-23/C AC220V 10S柜内板前接线

josef约瑟 时间继电器 DS-23/C AC220V 10S柜内板前接线

系列型号&#xff1a; DS-21时间继电器 &#xff1b;DS-22时间继电器&#xff1b; DS-23时间继电器&#xff1b;DS-24时间继电器&#xff1b; DS-21C时间继电器&#xff1b;DS-22C时间继电器&#xff1b; DS-23C时间继电器&#xff1b; DS-25时间继电器&#xff1b;DS-26…
阅读更多...
Delphi 编译关闭时 Stack overflow 错误

Delphi 编译关闭时 Stack overflow 错误

本人工程文件&#xff0c;编译EXE文件&#xff0c;程序关闭时出现 Stack overflow 错误。网搜索一些解决办法&#xff1a;比如&#xff0c;加大堆栈...&#xff0c;均不能问题。虽然&#xff0c;生成的EXE文件&#xff0c;执行时&#xff0c;无任何问题。 Stack overflow 错误&…
阅读更多...
【面试】测试/测开（NIG2）

【面试】测试/测开（NIG2）

145. linux打印前row行日志 参考&#xff1a;linux日志打印 前10行日志 head -n 10 xx.log后10行日志 tail -n 10 xx.log tail -10f xx.log使用sed命令 sed -n 9,10p xx.log #打印第9、10行使用awk命令 awk NR10 xx.log #打印第10行 awk NR>7 && NR<10 xx.log …
阅读更多...
基于JSP+Servlet+Mysql的建设工程监管信息

基于JSP+Servlet+Mysql的建设工程监管信息

基于JSPServletMysql的建设工程监管信息 一、系统介绍二、功能展示1.企业信息列表2.录入项目信息3.项目信息列表 四、其它1.其他系统实现五.获取源码 一、系统介绍 项目名称&#xff1a;基于JSPServlet的建设工程监管信息 项目架构&#xff1a;B/S架构 开发语言&#xff1a;…
阅读更多...
IEEE、Sci-Hub

IEEE、Sci-Hub

最近要写毕业论文&#xff0c;记录一下查询资料的网站。 IEEE&#xff08;Institute of Electrical and Electronics Engineers&#xff09;是世界上最大的专业技术协会之一&#xff0c;致力于推动电气和电子工程领域的创新和发展。IEEE成立于1884年&#xff0c;总部位于美国纽…
阅读更多...
【公务员】资料分析——做题技巧

【公务员】资料分析——做题技巧

小分互换 1 2 50 % 1 3 33.3 % 1 4 25 % 1 5 20 % 1 6 16.7 % 1 7 14.3 % 1 8 12.5 % 1 9 11.1 % 1 10 10 % 1 11 9.1 % 1 12 8.3 % 1 13 7.7 % 1 14 7.1 % 1 15 6.7 % \frac 1250\% \quad \frac 1333.3\% \quad \frac 1425\% \quad \frac 1520\% \quad \frac 16…
阅读更多...
基于CentOS7_安装Docker

基于CentOS7_安装Docker

基于CentOS7_安装Docker 配置网络&#xff0c;使其能ping通外网 安装依赖包 yum install -y yum-utils device-mapper-persistent-data lvm2下载repo文件 wget -O /etc/yum.repos.d/docker-ce.repo https://repo.huaweicloud.com/docker-ce/linux/centos/docker-ce.repo更换…
阅读更多...
基于Springboot的体育馆管理系统（有报告）。Javaee项目，springboot项目。

基于Springboot的体育馆管理系统（有报告）。Javaee项目，springboot项目。

演示视频&#xff1a; 基于Springboot的体育馆管理系统&#xff08;有报告&#xff09;。Javaee项目&#xff0c;springboot项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系结构&a…
阅读更多...
【Spring】Spring中的事务

【Spring】Spring中的事务

文章目录 1. Spring事务简介2. Spring事务的案例案例代码代码目录结构数据库pom.xmlResource/jdbc.propertiesconfig/SpringConfig.javaconfig/JdbcConfig.javaconfig/MyBatisConfig.javadao/AccountDao.javaservice/AccountService.javaservice/impl/AccountServiceImpl.java测…
阅读更多...
电子元器件介绍——电感（三）

电子元器件介绍——电感（三）

电子元器件 文章目录 电子元器件前言一、电感的基础知识二、电感的分类与作用三、电感的作用 总结 前言 这一节学习一下电感 一、电感的基础知识 电感是导线内通过交流电流时&#xff0c;在导线的内部及其周围产生交变磁通&#xff0c;导线的磁通量与生产此磁通的电流之比。…
阅读更多...
[python][plotly]利用plotly绘制散点图

[python][plotly]利用plotly绘制散点图

import plotly.express as px import pandas as pd# 创建示例数据 data pd.DataFrame({x: [1, 2, 3, 4, 5],y: [5, 4, 3, 2, 1] })# 使用 plotly.express 绘制散点图 fig px.scatter(data, xx, yy, titleScatter plot) fig.show() 结果&#xff1a;
阅读更多...
LabVIEW开发地铁运行安全监控系统

LabVIEW开发地铁运行安全监控系统

LabVIEW开发地铁运行安全监控系统 最近昌平线发生的故障事件引起了广泛关注&#xff0c;暴露了现有地铁运行监控系统在应对突发情况方面的不足。为了提高地铁系统的运行安全性&#xff0c;并防止类似事件再次发生&#xff0c;提出了一套全面的地铁运行安全监控系统方案。此方案…
阅读更多...
写好ChatGPT提示词原则之：清晰且具体（clear specific）

写好ChatGPT提示词原则之：清晰且具体（clear specific）

ChatGPT 的优势在于它允许用户跨越机器学习和深度学习的复杂门槛&#xff0c;直接利用已经训练好的模型。然而&#xff0c;即便是这些先进的大型语言模型也面临着上下文理解和模型固有局限性的挑战。为了最大化这些大型语言模型&#xff08;LLM&#xff09;的潜力&#xff0c;关…
阅读更多...
使用java获取nvidia显卡信息

使用java获取nvidia显卡信息

前言 AI开发通常使用到GPU&#xff0c;但通常使用的是python、c等语言&#xff0c;java用的则非常少。这也导致了java在gpu相关的库比较少。现在的需求是要获取nvidia显卡的使用情况&#xff0c;如剩余显存。这里给出两种较简单的解决方案。 基于nivdia-smi工具 显卡是硬件&a…
阅读更多...
检查数组中是否含有数据类型为复数的元素np.iscomplexobj()

检查数组中是否含有数据类型为复数的元素np.iscomplexobj()

【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 检查数组中是否含有 数据类型为复数的元素 np.iscomplexobj() [太阳]选择题 下列关于代码的说法正确的是&#xff1a; import numpy as np anp.array([1,23j]) bnp.array([1,2,3]) print(&quo…
阅读更多...
Python-数据分析可视化实例图

Python-数据分析可视化实例图

Python-数据分析可视化实例图 一&#xff1a;3D纹理图 运行效果图&#xff1a; Python代码&#xff1a; import math from typing import Unionimport pyecharts.options as opts from pyecharts.charts import Surface3Ddef float_range(start: int, end: int, step: Union[…
阅读更多...
整合SpringSecurity

整合SpringSecurity

目录 前言 数据库设计 用户表 角色表 用户角色表 权限表 角色权限表 插入数据 表的实体类 用户表实体类 角色表实体类 权限表实体类 mapper层接口 UserMapper RoleMapper AuthorityMapper 封装登录信息 统一响应结果 上下文相关类 jwt令牌工具类 依赖导入…
阅读更多...
[Verilog] Verilog 基本格式和语法

[Verilog] Verilog 基本格式和语法

主页&#xff1a; 元存储博客 全文 3000 字 文章目录 1. 声明格式1.1 模块声明1.2 输入输出声明1.3 内部信号声明1.4 内部逻辑声明1.5 连接声明1.6 数据类型声明1.7 运算符和表达式1.8 控制结构 2. 书写格式2.1 大小写2.2 换行2.3 语句结束符2.4 注释2.5 标识符2.6 关键字 1. 声…
阅读更多...
docker入门小结

docker入门小结

docker是什么&#xff1f;它有什么优势&#xff1f; 快速获取开箱即用的程序 docker使得所有的应用传输就像我们日常通过聊天工具文件传输一样&#xff0c;发送方将程序传输到超级码头而接收方也只需通过超级码头进行获取即可&#xff0c;就像一只鲸鱼拖着货物来回运输一样。…
阅读更多...
linux一次性调度执行_at命令

linux一次性调度执行_at命令

........................................................................................................................................................... 9.1 一次性调度执行 Schedule one-time tasks with at. ............................................…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023