前言
本文将会向你介绍哈希概念,哈希方法,如何解决哈希冲突,以及闭散列与开散列的模拟实现
1. 哈希概念
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即 O( l o g 2 N log_2N log2N),搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。
如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一 一映射的关系,那么在查找时通过该函数可以很快找到该元素。 当向该结构中: 插入元素根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放搜索元素
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功
该方式即为哈希方法,哈希方法中使用的转换函数称为哈希函数,构造出来的结构称为哈希表(Hash Table)(或者称散列表
例如:数据集合{1,7,6,4,5,9};
哈希函数设置为:hash(key) = key % size; size为存储元素底层空间总的大小。
2. 哈希方法
哈希方法:我们通常对关键码key进行转换来确定存储的位置,比如由字符串abc转换成一个整数作为存储的位置,这个转换的方法称为哈希方法,哈希方法中运用的函数叫做哈希函数
(1)直接定址法
ps:哈希方法是一个广义的概念,而哈希函数是哈希方法的一种具体实现。
1、直接定址法 值和位置关系唯一关系,每个值都有一个唯一位置,但是值很分散,直接定址会导致空间开很大,导致空间浪费
(此方法运用于关键字范围集中,量不大的情况,关键字和存储位置是一对一的关系,不存在哈希冲突)
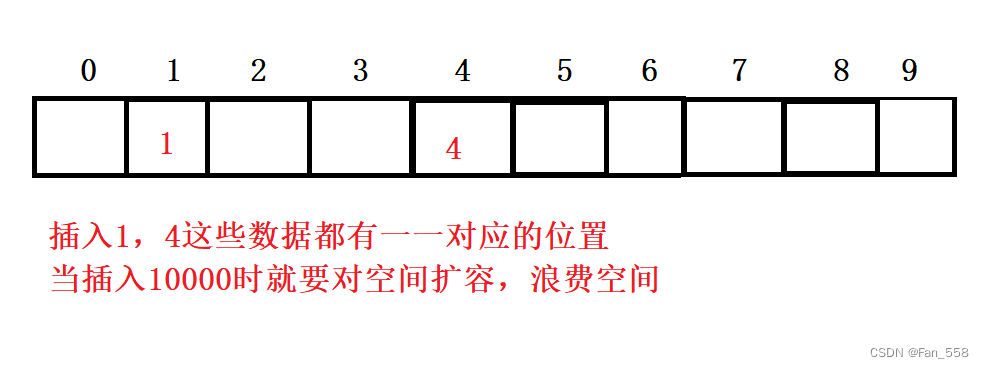
引入哈希冲突
哈希冲突概念:不同关键字通过相同的哈希函数计算出相同的哈希存储位置(不同的值映射到相同的位置上去),这种现象被称为哈希冲突或哈希碰撞,哈希冲突的发生与哈希函数的设计有关
(2)除留余数法
主要应用于关键字可以很分散,量可以很大,关键字和存储位置是多对一的关系的情况,但是存在哈希冲突
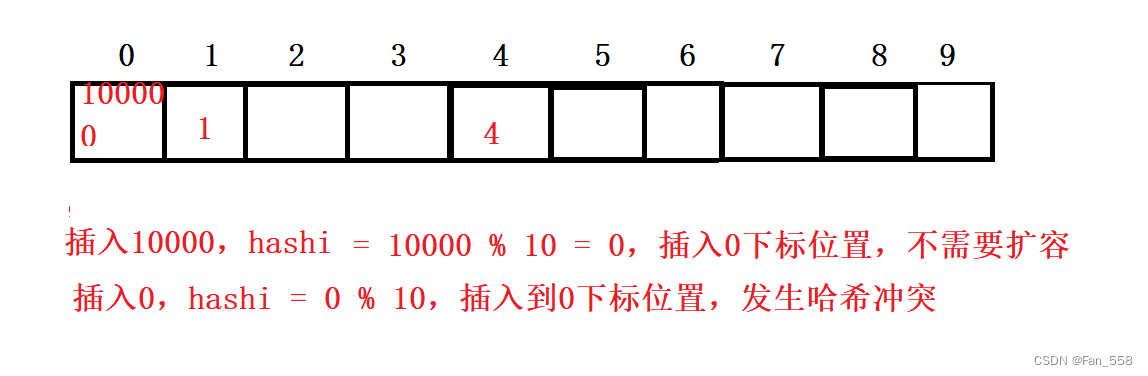
3. 解决哈希冲突
(1)闭散列
概念: 闭散列又称开放定址法,指当前位置被占用(哈希冲突),开放空间里按照某种规则,找一个没有被占用的位置存储
1、线性探测
从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止 Hashi = hashi + i(i>=0)
2、二次探测
探测公式发生变化 hashi + i^2(i>=0)
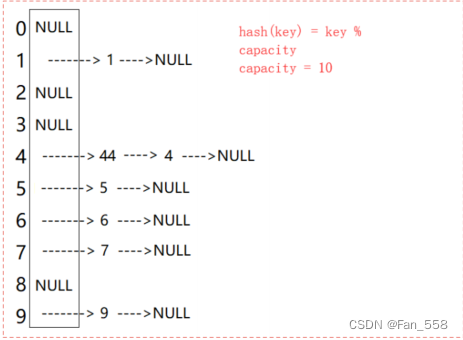
(2)开散列
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地
址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
如图可观察到,val值为44的节点和节点val值为4的节点发生哈希冲突
开散列中每个桶中放大都是发生哈希冲突的元素
引入负载因子
负载因子:存储个数/空间的大小(注意这里的空间的大小是size而不是capacity)
由于在哈希表中,operator[]操作会根据已有的元素数量(即size())进行检查。因此,在计算负载因子时,要使用已有元素的个数除以哈希表的大小(即size())
size()函数返回的是当前哈希表中实际存储的元素数量,而capacity()函数返回的是哈希表的容量(即内部存储空间的大小)
负载因子:存储关键字个数/空间大小 负载因子太大,冲突可能会剧增,冲突增加,效率降低 负载因子太小,冲突降低,但是空间利用率就低了
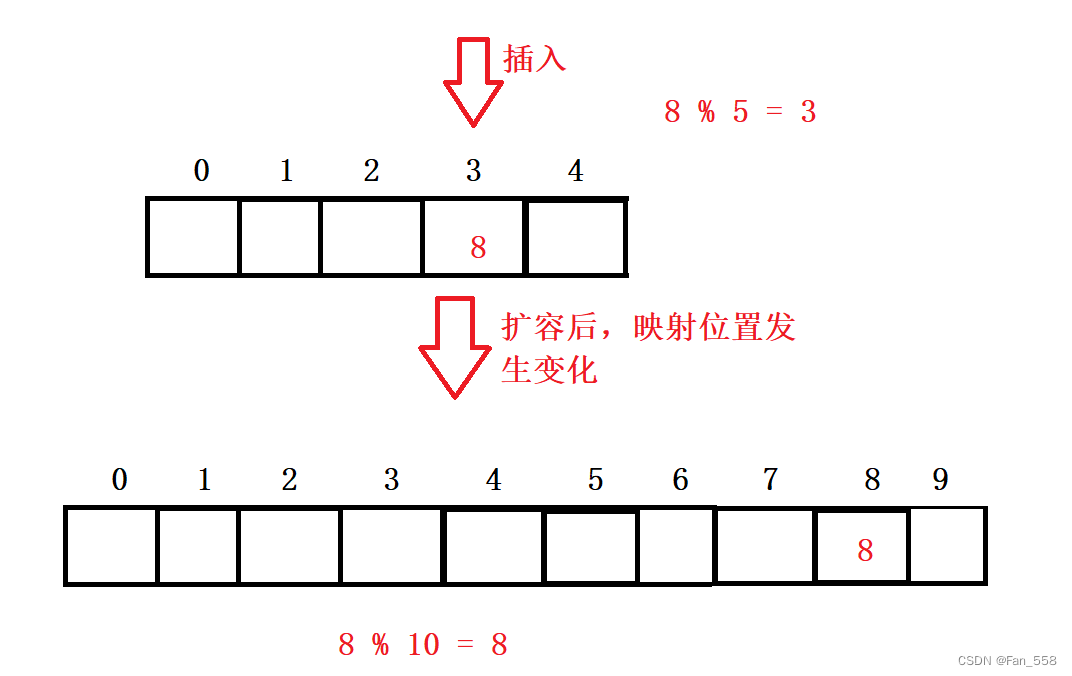
5. 哈希表扩容
扩容的核心是先开辟新空间,然后遍历旧空间的数据,按照hashi = hashi % Newsize重新建立映射,然后将旧空间的数据拷贝到新空间去,最后交换新旧哈希表,本质上我们还是要对旧哈希表进行扩容,因此最后要swap交换两表
6. 哈希表插入
三种状态EMPTY、EXIST、DELETE
EMPTY,表示该位置为空。
EXIST,表示该位置被占用了。
DELETE,表示该位置被删除了。
删除状态存在的含义
或许你会有疑问:删除为什么不能直接设为空状态,而是将被删除的状态设置为DELETE

7. 闭散列模拟实现
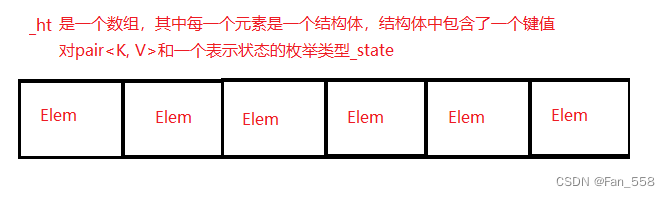
数据结构
struct Elem
{
pair<K, V> _val;
State _state = EMPTY;
};
vector<Elem<K, V>> _ht;
闭散列插入
闭散列的插入步骤是:判断是否存在,判断是否需要扩容(结合负载因子),遍历旧空间拷贝数据
关于闭散列的模拟实现,核心步骤在上文都有讲,这里就不再多作赘述,具体可看下面的代码与注释
namespace Close_Hash
{
template<class T>
struct HashFunc
{
size_t operator()(const T& key)
{
return (size_t)key;
}
};
//因为字符串做键值非常常见,库里面也特化了一份
//BKDR算法,这里不会展开来讲
template<>
struct HashFunc<string>
{
size_t operator()(const string& key)
{
size_t hashi = 0;
for (auto ch : key)
{
hashi = hashi * 31 + ch;
}
return hashi;
}
};
enum State
{
EMPTY
,EXIST
,DELETE
};
template <class K, class V>
struct Elem
{
pair<K, V> _val;
State _state = EMPTY;
};
template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
HashTable(size_t capacity = 3)
: _ht(capacity)
,_size(0)
, _totalSize(0)
{
for (size_t i = 0; i < capacity; ++i)
_ht[i]._state = EMPTY;
}
// 插入
bool Insert(const pair<K, V>& val)
{
Hash hf;
_size = _ht.size();
//已有
if (Find(val.first))
{
return false;
}
else
{
//扩容,负载因子==0.6
if ((double)_totalSize / _size >= 0.6)
{
//开辟新空间
size_t newsize = _size * 2;
HashTable<K, V, Hash> NewHt;
NewHt._ht.resize(newsize);
//遍历旧空间
for (int i = 0; i < _size; i++)
{
if (_ht[i]._state == EXIST)
{
NewHt.Insert(_ht[i]._val);
}
}
NewHt._ht.swap(_ht);
}
size_t hashi = hf(val.first) % _size;
//不为空,向后查找
while (_ht[hashi]._state == EXIST)
{
hashi++;
//如果超出数组长度
hashi %= _size;
}
//为空,插入
_ht[hashi]._val.first = val.first;
_ht[hashi]._val.second = val.second;
_ht[hashi]._state = EXIST;
++_totalSize;
return true;
}
}
// 查找
Elem<K, V>* Find(const K& key)
{
Hash hf;
//线性探测
size_t hashi = hf(key) % _ht.size();
while (_ht[hashi]._state != EMPTY)
{
if (_ht[hashi]._state == EXIST
&& _ht[hashi]._val.first == key)
{
return &_ht[hashi];
}
hashi++;
//超出数组长度
hashi %= _ht.size();
}
//没有找到a
return nullptr;
}
// 删除
bool Erase(const K& key)
{
Elem<K, V>* ret = Find(key);
//不为空就说明找到
if (ret)
{
ret->_state = DELETE;
--_totalSize;
return true;
}
else return false;
}
private:
size_t HashFunc(const K& key)
{
return key % _ht.capacity();
}
void CheckCapacity();
private:
vector<Elem<K, V>> _ht;
size_t _size;
size_t _totalSize; // 哈希表中的所有元素:有效和已删除, 扩容时候要用到
};
}
测试
void Print()
{
for (int i = 0; i < _ht.size(); i++)
{
if (_ht[i]._state == EXIST)
{
//printf("[%d]->%d\n", i, _tables[i]._kv.first);
cout << "[" << i << "]->" << _ht[i]._val.first << ":" << _ht[i]._val.second << endl;
}
else if (_ht[i]._state == EMPTY)
{
printf("[%d]->\n", i);
}
else
{
printf("[%d]->D\n", i);
}
}
void TestHT1()
{
Close_Hash::HashTable<int, int> ht;
int a[] = { 4,14,24,34,5,7,1 };
for (auto e : a)
{
ht.Insert(make_pair(e, e));
}
ht.Print();
ht.Insert(make_pair(3, 3));
ht.Insert(make_pair(3, 3));
ht.Insert(make_pair(-3, -3));
ht.Print();
cout << endl;
ht.Erase(3);;
ht.Print();
if (ht.Find(3))
{
cout << "3存在" << endl;
}
else
{
cout << "3不存在" << endl;
}
ht.Insert(make_pair(23, 3));
ht.Insert(make_pair(3, 3));
if (ht.Find(3))
{
cout << "3存在" << endl;
}
else
{
cout << "3不存在" << endl;
}
ht.Print();
}
8. 开散列模拟实现
数据结构
struct HashNode
{
HashNode* _next;
pair<K, V> _val;
HashNode(const pair<K, V>& val)
:_next(nullptr)
,_val(val)
{}
};
typedef HashNode<K, V> Node;
vector<Node*> _ht;
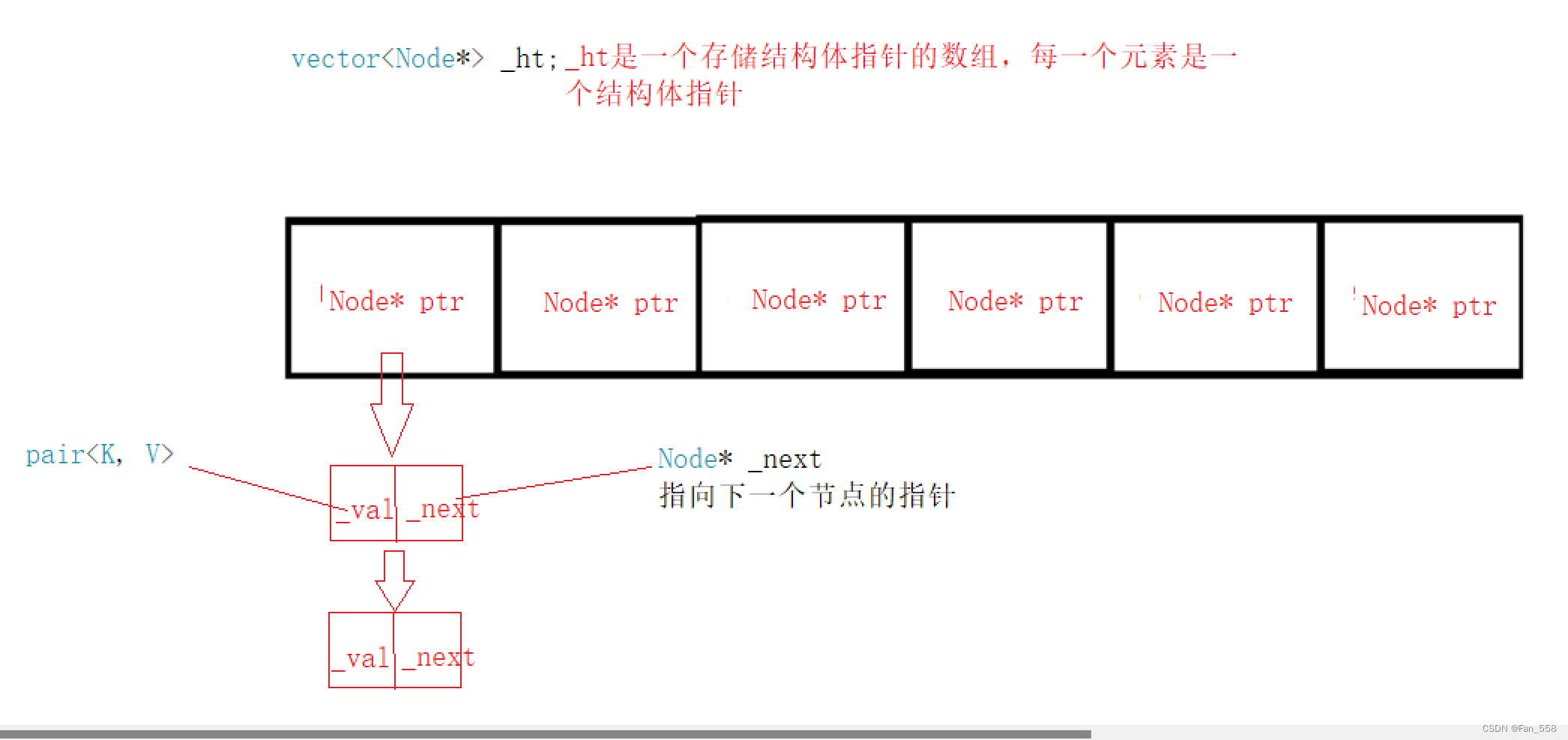
开散列插入
插入的主要逻辑是:先查找是否存在,判断是否需要扩容(依据平衡因子),开辟新空间然后遍历旧空间,将旧空间的数据拷贝到新空间上(需要根据新的映射关系,待会会细讲),最后插入节点
bool Insert(const pair<K, V>& val)
{
Hash hf;
//已有
if (Find(val.first))
{
return false;
}
//扩容,负载因子==1
if (_totalSize == _ht.size())
{
//开辟新空间
size_t newsize = _ht.size() * 2;
vector<Node*> NewHt;
NewHt.resize(newsize);
//遍历旧空间
for (int i = 0; i < _ht.size(); i++)
{
Node* cur = _ht[i];
while (cur)
{
//保存下一个结构体指针
Node* next = cur->_next;
size_t hashi = hf(cur->_val.first) % NewHt.size();
//将新空间上hashi位置处的哈希桶链接到需要处理的当前节点
cur->_next = NewHt[hashi];
NewHt[hashi] = cur;
//处理旧空间上哈希桶的下一个节点
cur = next;
}
//防止出现悬空指针的问题
_ht[i] = nullptr;
}
_ht.swap(NewHt);
}
//插入节点
size_t hashi = hf(val.first) % _ht.size();
Node* newnode = new Node(val);
//头插
newnode->_next = _ht[hashi];
_ht[hashi] = newnode;
++_totalSize;
return true;
}
以下是遍历旧空间,拷贝数据的图解
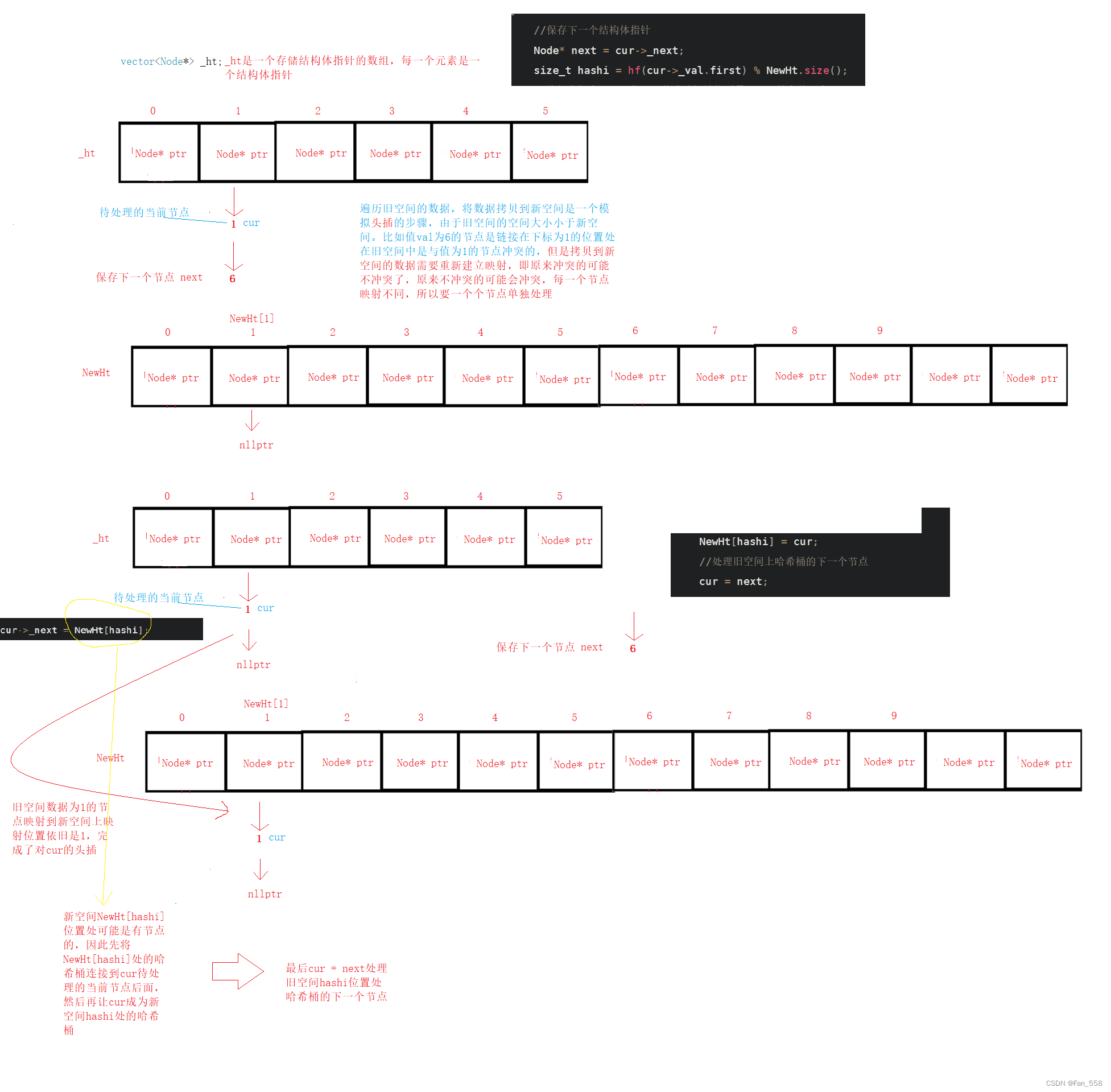
插入过程图解
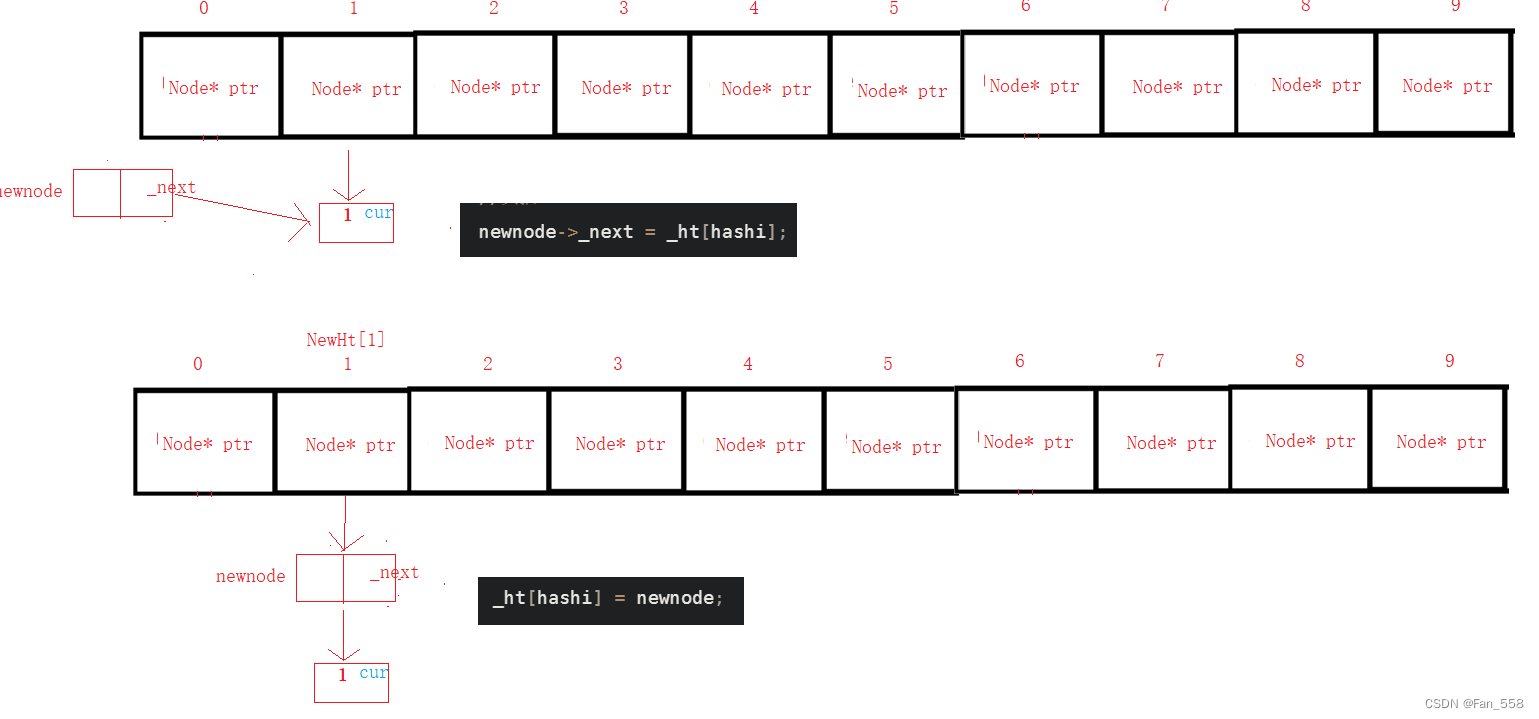
全部代码
namespace Open_Hash
{
template<class T>
struct HashFunc
{
size_t operator()(const T& key)
{
if (key >= 0)
{
return (size_t)key;
}
else
{
return abs(key);
}
}
};
//字符串哈希算法这里不展开讲,采用的是BKDR算法
template<>
struct HashFunc<string>
{
size_t operator()(const string& key)
{
size_t hashi = 0;
for (auto ch : key)
{
hashi = hashi * 31 + ch;
}
return hashi;
}
};
template <class K, class V>
struct HashNode
{
HashNode* _next;
pair<K, V> _val;
HashNode(const pair<K, V>& val)
:_next(nullptr)
,_val(val)
{}
};
template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
HashTable()
{
_ht.resize(10);
}
~HashTable()
{
for (int i = 0; i < _ht.size(); i++)
{
Node* cur = _ht[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
//将当前哈希桶置空
_ht[i] = nullptr;
}
}
typedef HashNode<K, V> Node;
// 插入
bool Insert(const pair<K, V>& val)
{
Hash hf;
//已有
if (Find(val.first))
{
return false;
}
//扩容,负载因子==1
if (_totalSize == _ht.size())
{
//开辟新空间
size_t newsize = _ht.size() * 2;
vector<Node*> NewHt;
NewHt.resize(newsize);
//遍历旧空间
for (int i = 0; i < _ht.size(); i++)
{
Node* cur = _ht[i];
while (cur)
{
//保存下一个结构体指针
Node* next = cur->_next;
size_t hashi = hf(cur->_val.first) % NewHt.size();
//将新空间上hashi位置处的哈希桶链接到需要处理的当前节点
cur->_next = NewHt[hashi];
NewHt[hashi] = cur;
//处理旧空间上哈希桶的下一个节点
cur = next;
}
//防止出现悬空指针的问题
_ht[i] = nullptr;
}
_ht.swap(NewHt);
}
//插入节点
size_t hashi = hf(val.first) % _ht.size();
Node* newnode = new Node(val);
//头插
newnode->_next = _ht[hashi];
_ht[hashi] = newnode;
++_totalSize;
return true;
}
//查找
Node* Find(const K& key)
{
Hash hf;
//线性探测
size_t hashi = hf(key) % _ht.size();
Node* cur = _ht[hashi];
//遍历对应hashi位置处的哈希桶
while (cur)
{
if (cur->_val.first == key)
{
return cur;
}
cur = cur->_next;
}
//没有找到
return nullptr;
}
// 删除
bool Erase(const K& key)
{
Hash hf;
Node* ret = Find(key);
size_t hashi = hf(key) % _ht.size();
//不为空就说明找到
if (ret)
{
Node* cur = _ht[hashi];
Node* prev = nullptr;
//遍历当前哈希桶
while (cur)
{
if (cur->_val.first == key)
{
//判断是头删还是中间位置处的删除
if (prev == nullptr)
{
_ht[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
}
//未找到
return false;
}
private:
vector<Node*> _ht;
Node* _next = nullptr;
size_t _totalSize = 0; // 哈希表中的所有元素:有效和已删除, 扩容时候要用到
};
}
测试
//打印
void Print1()
{
for (int i = 0; i < _ht.size(); i++)
{
Node* cur = _ht[i];
cout << "[" << i << "]:";
//哈希桶不为空
while(cur)
{
cout << "(" << cur->_val.first << "," << cur->_val.second << ")" << "->";
cur = cur->_next;
}
cout << endl;
}
cout << endl;
}
void Print2()
{
for (int i = 0; i < _ht.size(); i++)
{
Node* cur = _ht[i];
//哈希桶不为空
while (cur)
{
cout << cur->_val.first << ":"<< cur->_val.second << " ";
cur = cur->_next;
}
}
cout << endl;
}
//测试
void TestHT1()
{
HashTable<int, int> ht;
int a[] = { 4,14,24,34,5,7,1 };
for (auto e : a)
{
ht.Insert(make_pair(e, e));
}
ht.Insert(make_pair(3, 3));
ht.Insert(make_pair(3, 3));
ht.Insert(make_pair(-3, -3));
ht.Print1();
ht.Erase(3);
ht.Print1();
if (ht.Find(3))
{
cout << "3存在" << endl;
}
else
{
cout << "3不存在" << endl;
}
ht.Insert(make_pair(3, 3));
ht.Insert(make_pair(23, 3));
//ht.Insert(make_pair(-9, -9));
ht.Insert(make_pair(-1, -1));
ht.Print1();
}
void TestHT2()
{
string arr[] = { "香蕉", "甜瓜","苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
//HashTable<string, int, HashFuncString> ht;
HashTable<string, int> ht;
for (auto& e : arr)
{
//auto ret = ht.Find(e);
HashNode<string, int>* ret = ht.Find(e);
if (ret)
{
ret->_val.second++;
}
else
{
ht.Insert(make_pair(e, 1));
}
}
ht.Print2();
ht.Insert(make_pair("apple", 1));
ht.Insert(make_pair("sort", 1));
ht.Insert(make_pair("abc", 1));
ht.Insert(make_pair("acb", 1));
ht.Insert(make_pair("aad", 1));
ht.Print2();
}
void Some()
{
const size_t N = 100;
vector<int> v;
v.reserve(N);
srand(time(0));
for (size_t i = 0; i < N; ++i)
{
//v.push_back(rand()); // N比较大时,重复值比较多
v.push_back(rand()%100+i); // 重复值相对少
//v.push_back(i); // 没有重复,有序
}
HashTable<int, int> ht;
for (auto e : v)
{
ht.Insert(make_pair(e, e));
}
ht.Print1();
}
小结
今日的分享就到这里啦,后续将会向你带来位图与布隆过滤器的知识,如果本文存在疏漏或错误的地方还请您能够指出,另外如果你存在疑问,也可以评论留言哦!


![[C++] 虚函数、纯虚函数和虚析构(virtual)](https://img-blog.csdnimg.cn/329c1550ce3545f0bc94b428d9c31c2d.png)