一、最小生成树

生成树中边的权值（代价）之和最小的树。

二、Prim算法

1. 算法思想

• 设N=(V,{E})是连通网，TE是N上最小生成树中边的集合；
• Step1:令U={u}，u∈V，TE={}；
• Step2:在u∈U,v∈V-U的边(u,v)∈E中找一条代价最小的边(u,v)并入TE,v并入U；
• Step3:重复Step2，直至U=V，T={U,{TE}}是N的最小生成树；
  

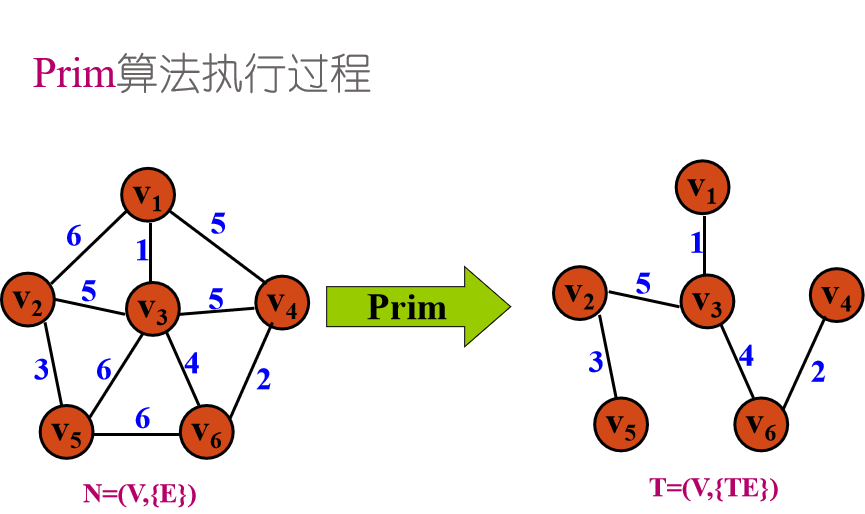
2. 例题

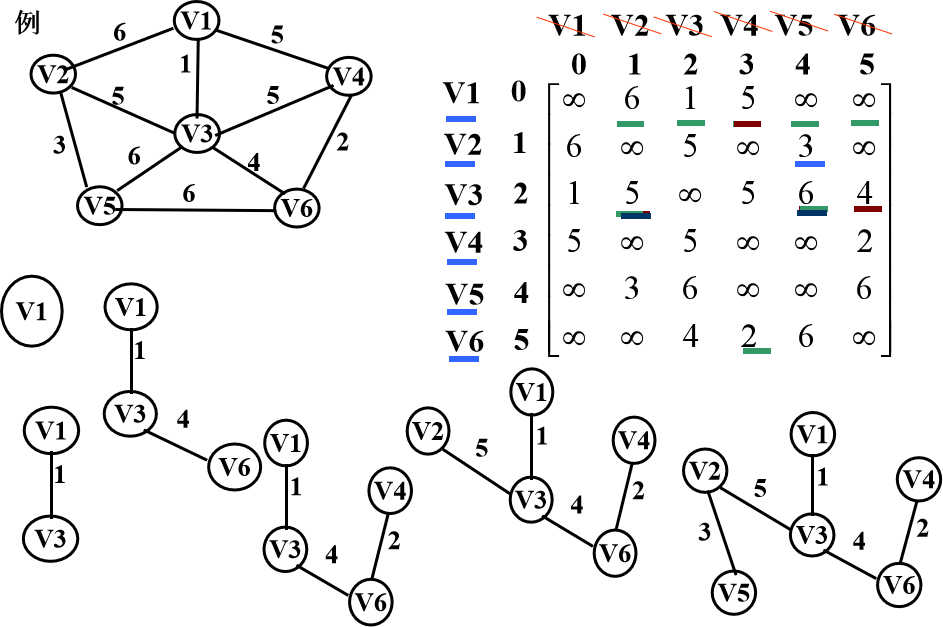
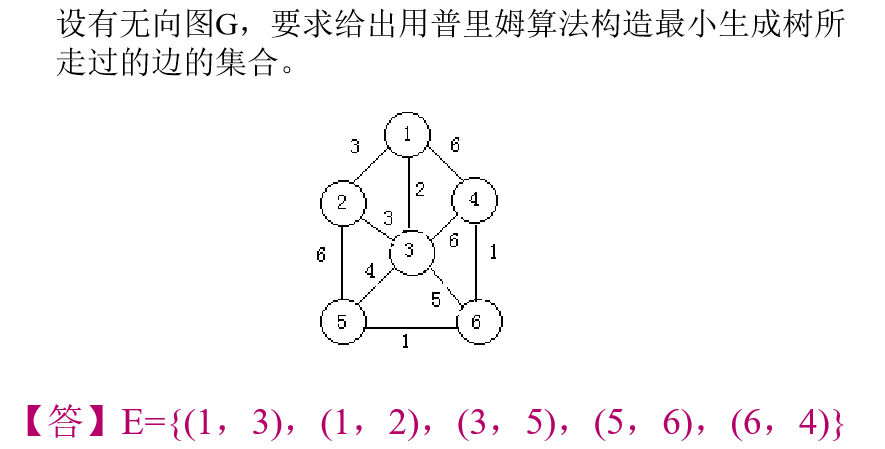
3. 性能分析

• 时间复杂度：O($n^2$) , 与网中的边数无关；
• 适用于求边稠密的网的最小生成树；

三、Kruscal算法

1. 算法思想

• 最小生成树上边权值之和最小，应使树上每一条边的权值尽量小；
• Step1:令最小生成树T的初态为只有n个顶点的非连通图T=(V,{})；
• Step2:从权值最小的边(u,v)开始，若该边依附的顶点落在TE的不同连通分量上，E=TE∪(u,v)，否则选择下一条代价最小的边；
• Step3:重复Step2，直至T所有顶点在同一连通分量上；

2. 例题

3. 性能分析

• 时间复杂度：O( e*log2e )；
• 适合于求边稀疏的网的最小生成树；