꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏:xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!

一.栈(Stack)
1.概念
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈
2.栈的模拟实现

可以看出栈Stack 是继承与Vector的, Vector和ArrayList类似,我们可以得到以下的栈的模拟实现,帮助我们更好的理解栈的使用。
//这是栈内存储Integer的模拟,当然栈是泛型,这里只是Integer的模拟
class MyStack {
public int[] arr;
public int size;
public MyStack() {
arr = new int[10];
}
//入栈
public int push(int e) {
ensureCapacity();
arr[size++] = e;
return e;
}
//判断栈是否满
private void ensureCapacity() {
if (size == arr.length) {
arr = Arrays.copyOf(arr, size * 2);
}
}
//栈顶元素
public int peek() {
if(empty()) {
System.out.println("栈为空,无元素");
return -1;
}
return arr[size-1];
}
//出栈
public int pop() {
int tmp = peek();
size--;
return tmp;
}
//判断栈是否为空
public boolean empty() {
return this.size == 0;
}
}3.栈、虚拟机栈、栈帧有什么区别呢
栈、虚拟机栈和栈帧是计算机科学中的概念,它们之间有以下区别:
-
栈:栈是一种具有后进先出(Last-In-First-Out,LIFO)特性的数据结构,可以存储和检索数据。在计算机中,栈通常用于管理函数调用和局部变量的分配。栈在内存中是连续存储的一块区域,主要用于存储函数调用的上下文信息以及局部变量。
-
虚拟机栈:虚拟机栈是Java虚拟机(JVM)为每个线程分配的内存区域,用于存储方法的调用和执行信息。每个线程在执行方法时,都会在虚拟机栈中创建一个栈帧,栈帧中包含了方法的局部变量、操作数栈、方法返回地址等信息。
-
栈帧:栈帧是方法在虚拟机栈中的表示,用于存储方法的局部变量、操作数栈、方法返回地址等信息。每个方法在执行时,都会在虚拟机栈中创建一个对应的栈帧,方法的参数、局部变量以及中间计算结果都存储在栈帧中。当方法执行完毕后,对应的栈帧就会被销毁。
总结来说,栈是一种数据结构,用于存储和检索数据;虚拟机栈是Java虚拟机为每个线程分配的内存区域,用于存储方法的调用和执行信息;栈帧是方法在虚拟机栈中的表示,用于存储方法的局部变量、操作数栈、方法返回地址等信息。
4.栈的应用
155.最小栈

题目分析:
我们都知道栈是一个先进后出的数据结构,所以我们只使用一个普通栈是无法实现最小栈,应该要用两个栈来模拟实现最小栈。
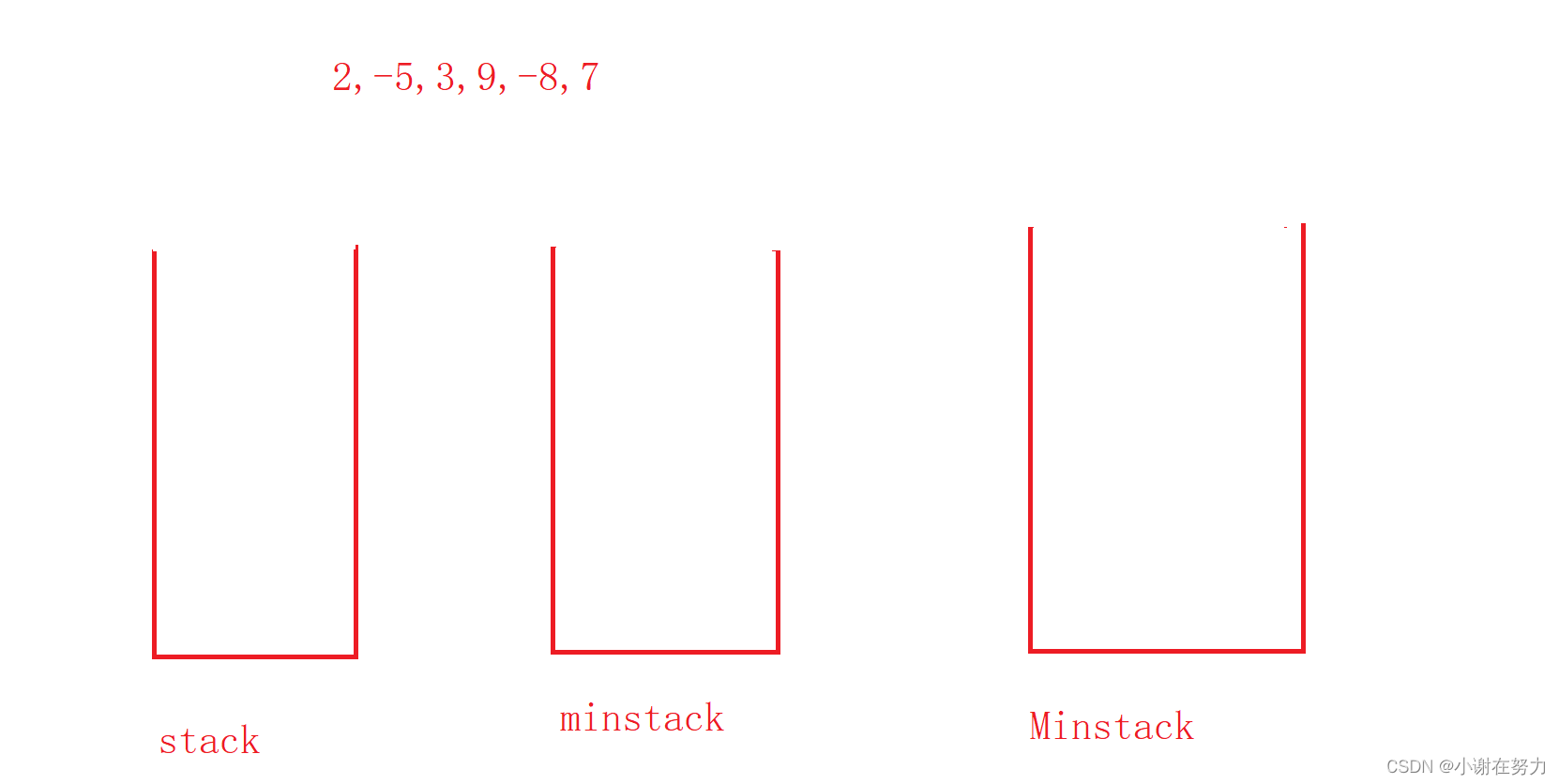
如果两个栈都为空就先将元素入栈
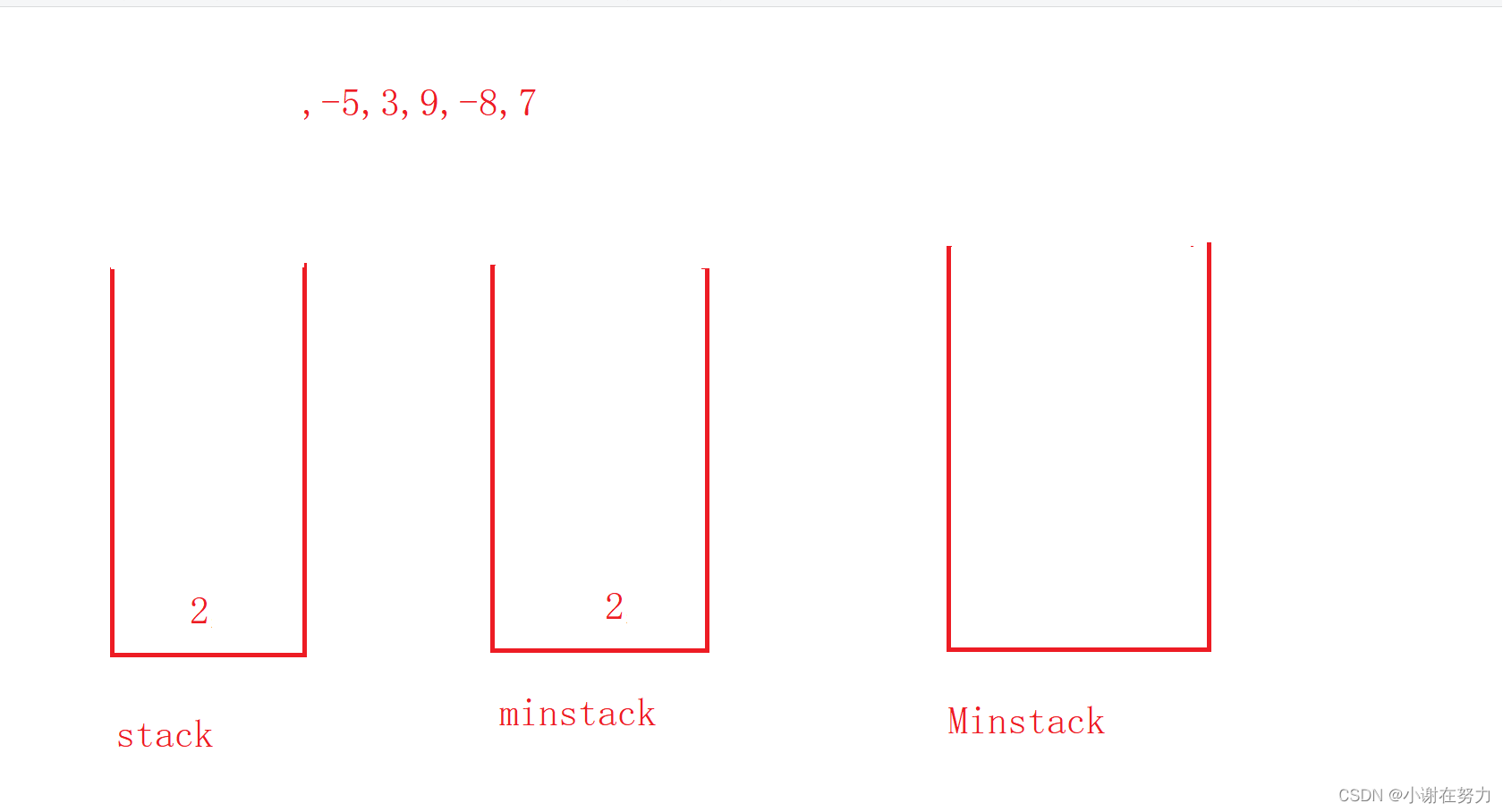
然后下一个元素先入stack 栈 之后和minstack 比较如果 < minstack的栈顶元素,就入 minstack 否则就不入,
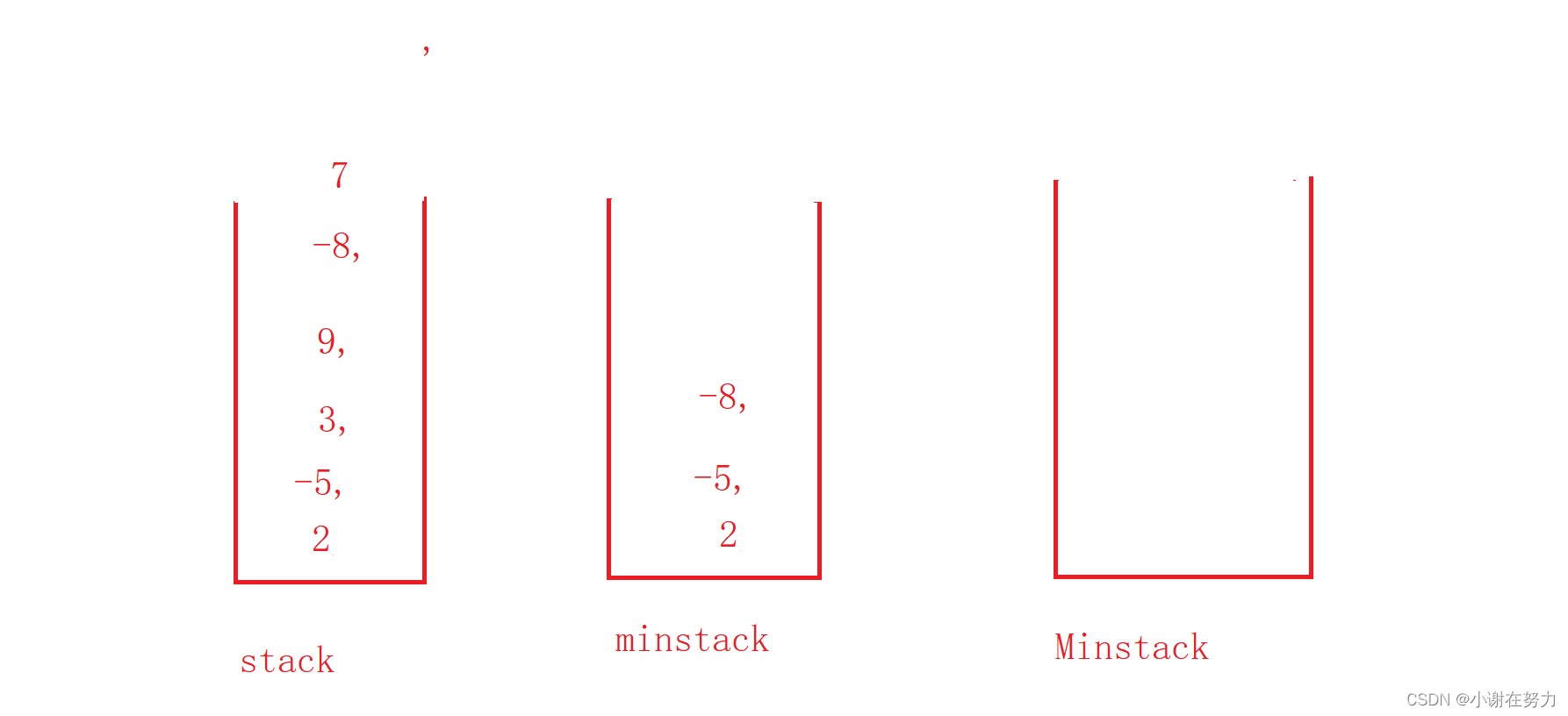
这样就通过用两个普通栈模拟最小栈了
class MinStack {
Stack<Integer> stack;
Stack<Integer> minstack;
public MinStack() {
stack = new Stack<>();
minstack = new Stack<>();
}
public void push(int val) {
stack.push(val);
if(minstack.empty()) {
minstack.push(val);
}else {
if(minstack.peek() >= val) {
minstack.push(val);
}
}
}
public void pop() {
int tmp = stack.pop();
if(tmp == minstack.peek()) {
minstack.pop();
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return minstack.peek();
}
}1.面试进阶
是否可以不用辅助栈呢
栈中每个元素代表的是要压入元素与当前栈中最小值的差值 有个很重要问题: 在弹出时如何维护min? 因为每次压入新的元素时,压入的都是与当前栈中最小值的差值(还未压入当前元素),故在弹出元素时,若弹出了当前最小值,因为栈中记录了当前元素与【之前】最小值的差值,故根据这个记录可以更新弹出元素后的最小值。 接下来看代码吧
class MinStack {
// 记录每个元素与【未压入】该元素时栈中最小元素的差值
LinkedList<Long> stack;
// 当前【已压入】栈中元素的最小值
private long min;
public MinStack() {
stack = new LinkedList();
}
public void push(int val) {
// 压入第一个元素
if(stack.isEmpty()){
min = val;
stack.addFirst(0L);
return;
}
// 栈不为空时,每次压入计算与min的差值后压入结果
stack.push((long)val-min);
// 更新min
min = Math.min((long)val,min);
// 上面两个语句是不能颠倒的!一定是先压入,在更新,因为min一定是当前栈中的最小值
}
public void pop() {
long pop = stack.removeFirst();
// 当弹出元素小于0时,说明弹出元素是当前栈中的最小值,要更新最小值
if(pop<0){
// 因为对于当前弹出的元素而言,计算压入栈中的值时,计算的是该元素与【未压入】该元素时
// 栈中元素的最小值的差值,故弹出该元素后栈中的最小值就是未压入该元素时的最小值
// 即当前元素的值(min)减去两者的差值
long lastMin = min;
min = lastMin - pop;
}
// 若大于等于0,不会对min有影响
}
public int top() {
long peek = stack.peek();
// 若当前栈顶小于等于0,说明最小值就是栈顶元素
if(peek<=0) return (int)min;
// 否则就是min+peek
return (int)(min+peek);
}
public int getMin() {
return (int)min;
}
}二.队列
1.概念
2.队列的模拟实现
public class Queue {
private int maxSize;
private int[] queueArray;
private int front;
private int rear;
private int nItems;
public Queue(int size) {
maxSize = size;
queueArray = new int[maxSize];
front = 0;
rear = -1;
nItems = 0;
}
public void insert(int value) {
if (rear == maxSize - 1) {
rear = -1;
}
queueArray[++rear] = value;
nItems++;
}
public int remove() {
int temp = queueArray[front++];
if (front == maxSize) {
front = 0;
}
nItems--;
return temp;
}
public int peek() {
return queueArray[front];
}
public boolean isEmpty() {
return (nItems == 0);
}
public boolean isFull() {
return (nItems == maxSize);
}
public int size() {
return nItems;
}
}
三.面试题
用队列实现栈
大家都清楚栈是先进后出,队列是先进先出的数据结构,如果要用队列模拟实现栈,仅靠一个队列是无法实现,需要用到两个队列,来模拟模拟实现栈

如果两个队列都为空 就入q1 的队
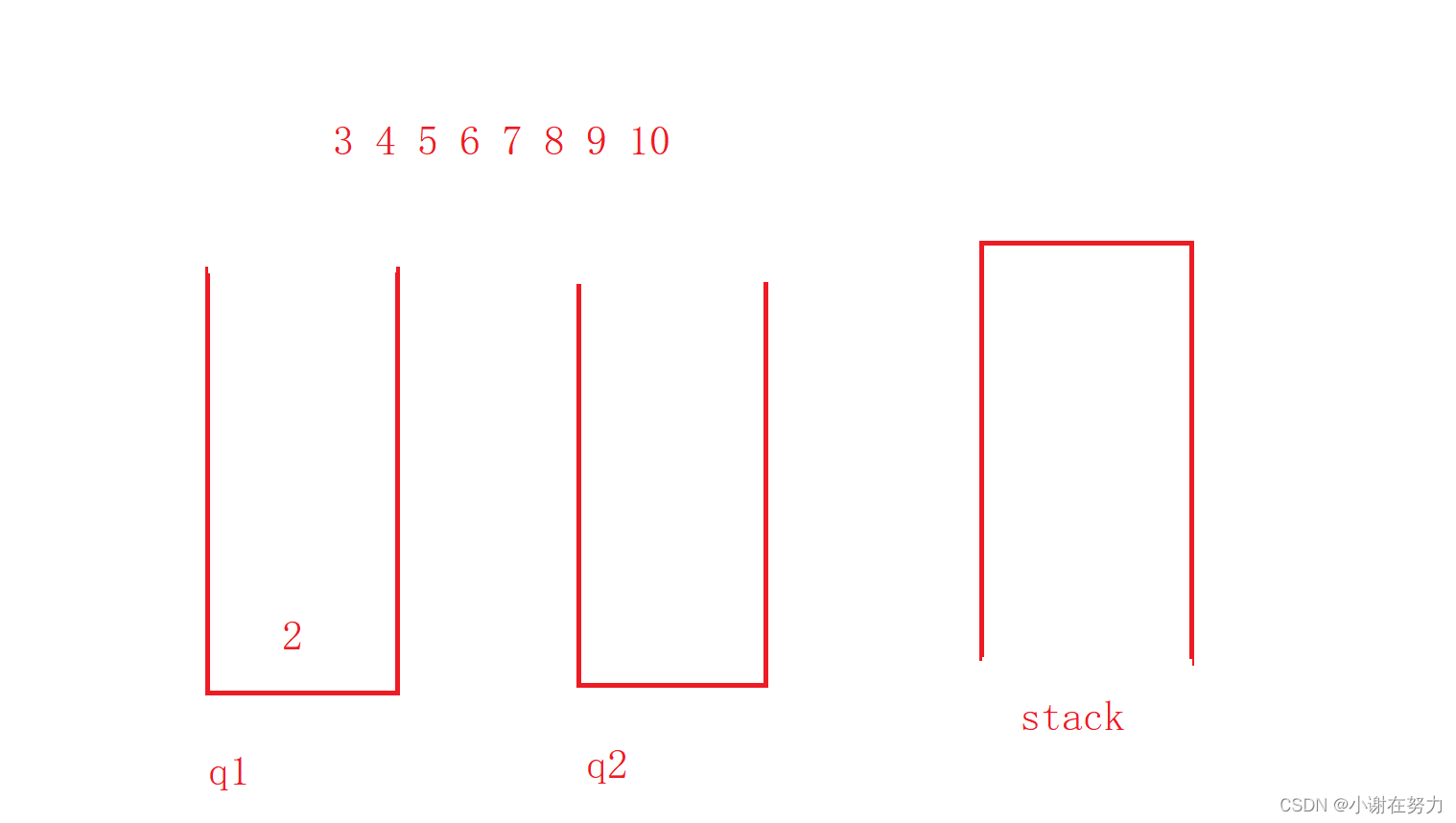
谁不为空就入队那个队列,如果要出栈的话,就把除了要出栈的那个元素之外的元素,入到另一个 队列中。

代码如下
class MyStack {
Queue<Integer> q1;
Queue<Integer> q2;
public MyStack() {
q1 = new LinkedList<>();
q2 = new LinkedList<>();
}
public void push(int x) {
if(empty()) {
q1.add(x);
return;
}if( ! q1.isEmpty()) {
q1.add(x);
}else {
q2.add(x);
}
}
public int pop() {
if(empty()) return -1;
if(!q1.isEmpty()) {
int size1 = q1.size();
for (int i = 0;i < size1-1;i++) {
q2.add(q1.poll());
}
return q1.poll();
}else {
int size2 = q2.size();
for (int i = 0; i < size2-1; i++) {
q1.add(q2.poll());
}
return q2.poll();
}
}
public int top() {
if(empty()) {
return -1;
}int temp = -1;
if(!q1.isEmpty()) {
int size2 = q1.size();
for(int i = 0; i < size2;i++) {
temp = q1.poll();
q2.offer(temp);
}
return temp;
}else {
int size2 = q2.size();
for(int i = 0;i < size2; i++) {
temp = q2.poll();
q1.offer(temp);
}
return temp;
}
}
public boolean empty() {
return q1.isEmpty() && q2.isEmpty();
}
}
用栈实现队列
栈实现队列的出队操作效率低下:栈底元素(对应队首元素)无法直接删除,需要将上方所有元素出栈。
两个栈可实现将列表倒序:设有含三个元素的栈 A = [1,2,3] 和空栈 B = [] 。若循环执行 A 元素出栈并添加入栈 B ,直到栈 A 为空,则 A = [] , B = [3,2,1] ,即栈 B 元素为栈 A 元素倒序。
利用栈 B 删除队首元素:倒序后,B 执行出栈则相当于删除了 A 的栈底元素,即对应队首元素。
因此,可以设计栈 A 用于加入队尾操作,栈 B 用于将元素倒序,从而实现删除队首元素。
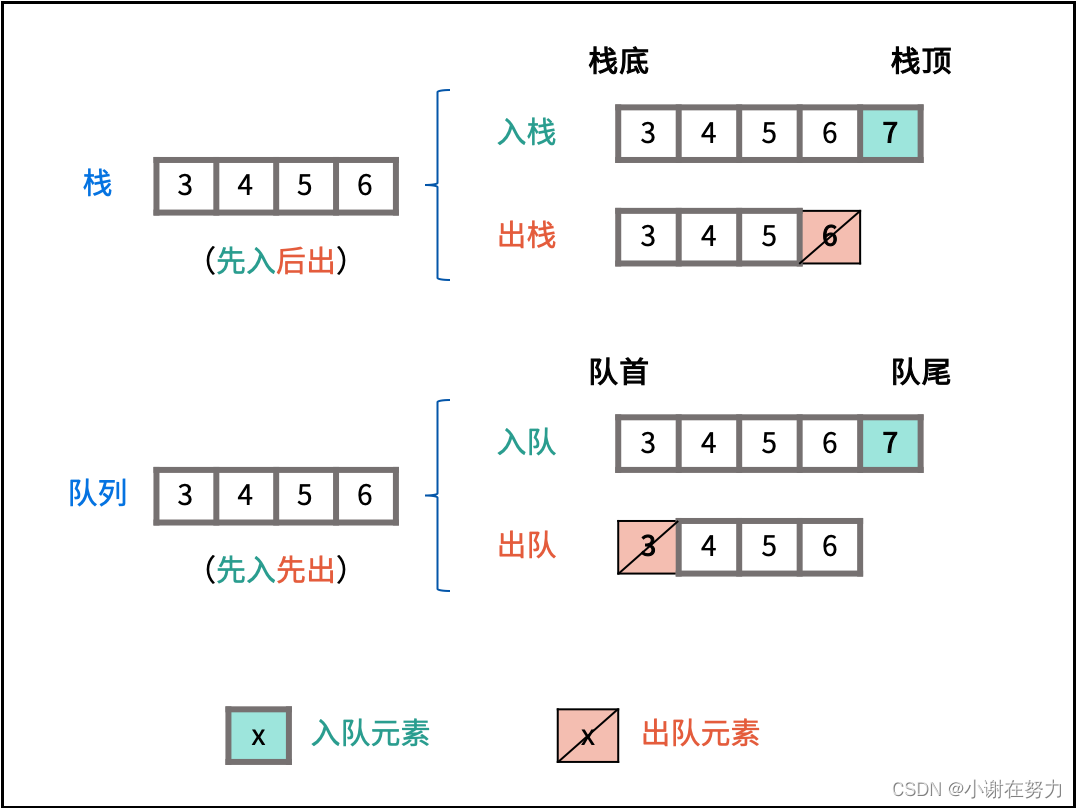
代码如下
class MyQueue {
Stack<Integer> s1;
Stack<Integer> s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
public void push(int x) {
s1.push(x);
}
public int pop() {
if(s2.empty()) {
while(!s1.empty()) {
s2.push(s1.pop());
}
}
return s2.pop();
}
public int peek() {
if(s2.empty()){
while(!s1.empty()){
s2.push(s1.pop());
}
}
return s2.peek();
}
public boolean empty() {
return s1.empty() && s2.empty();
}
}以上就是栈和队列的所有内容了,在这里博主还是要说一句,要想理解栈和队列还是要多多刷类似的题目,一定可以更好的理解他们的使用
![[C++] 虚函数、纯虚函数和虚析构(virtual)](https://img-blog.csdnimg.cn/329c1550ce3545f0bc94b428d9c31c2d.png)