Renyi散度：Renyi divergence

news2024/11/17 9:25:41

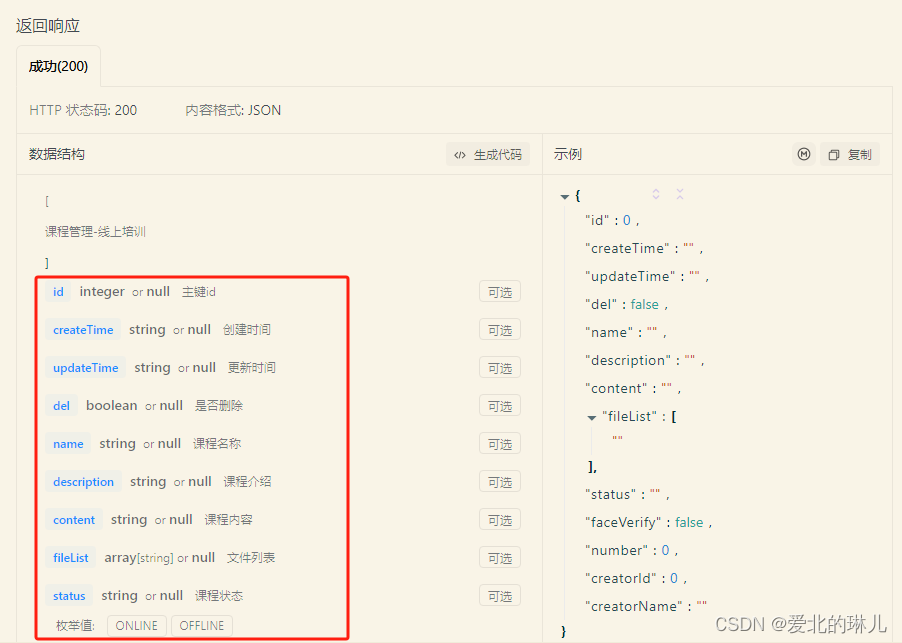
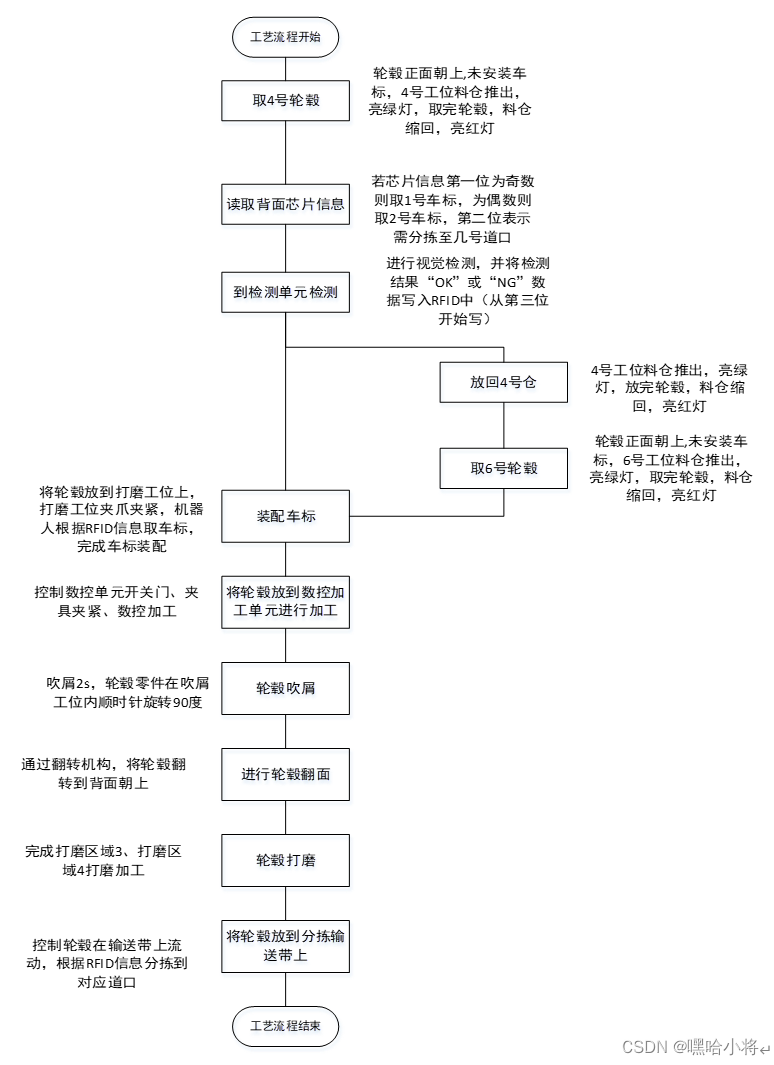
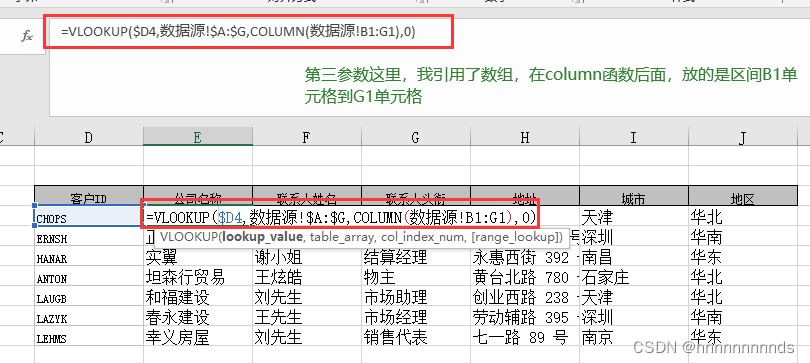
有关Renyi散度的基本介绍挺多博客已经写了。本文章主要介绍最基础的概念，以及近些年论文中为啥老喜欢引用这个概念。

一.基础概念

Renyi散度主要是描述两个分布之间的关系。对一个离散的概率分布X，其定义域记作 $Supp(X)$ ，其实就是概率不为零的点的集合。形式化的定义如下：

Let $X(E)$ denote the probability that event E occurs under distribution χ. We let $Supp(X)=\lbrace x:X(x)\neq0\rbrace$

对于两个离散的概率分布P和Q，假定 $Supp(P)\subset Supp(Q)$ （其实就是Q的取值更多），2阶Renyi散度定义如下：

$RD_2(P||Q)=\sum_{x\in Supp(P)}\frac{P(x)^2}{Q(x)}$

二. 论文常用的Renyi散度结论

性质1：对分布进行确定的函数变换，只会降低Renyi散度。

对于两个离散的概率分布P和Q，假定 $Supp(P)\subset Supp(Q)$ ，对任意给定的函数f，都有：

$RD_2(f(P)||f(Q))\leq RD_2(P||Q)$

性质2：可忽略性质的传递（计算复杂性理论）

对于两个离散的概率分布P和Q，假定 $Supp(P)\subset Supp(Q)$ ，从分布Q中取子事件 $E\subset Supp(Q)$ ，都有：

$Q(E)\geq P(E)^2/RD_2(P||Q)$

这个性质其实在密码学中很有用，为啥这么讲呢。如果可以证明 $RD_2(P||Q)$ 的上界为多项式。那么当事件E在分布Q中发生的概率 $Q(E)$ 可忽略，就可以推出事件E在分布P中发生的概率也可忽略。

性质3：Renyi散度与离散的高斯分布（格密码中的概念）

接触过格密码（参考我之前介绍过格密码）的人可能见过一个符号 $D_{Z_q,\sigma}^m$ ，这个符号啥意思呢？D代表离散的高斯分布， $Z_q$ 代表该高斯分布的取值全为整数模q， $\sigma$ 代表离散高斯分布的标准差，m代表维度，也就是：

$D_{Z_q,\sigma}^m$ ：关于原点对称的m维离散高斯分布

给一个不太大的数e，那么：

$(e+D_{Z_q,\sigma})^m$ ：中心点略微偏移原点的m维离散高斯分布。

好了，现在可以解释第三个性质了。

固定三个整数 $m,q,\lambda\in Z$ ，有一个上限值 $\beta_{Renyi}$ ，离散高斯分布的标准差满足 $\beta_{Renyi}\leq\sigma\leq q$ 。令 $e\in Z$ ，且满足 $|e|\leq \beta_{Renyi}$ ，那么有：
$RD_2((e+D_{Z_q,\sigma})^m||D_{Z_q,\sigma}^m)\leq exp(2\pi m(\beta_{Renyi/\sigma})^2)$

这个性质看起来有点长，其实是想解释把离散高斯分布平移一点点后，该分布与原始的离散高斯分布的Renyi散度是有上界的。密码学非常关注多项式，指数，次指数等复杂度，利用该定理，比如令离散高斯分布的标准差 $\sigma=\Omega(\beta_{Renyi}\sqrt{m/log\lambda})$ 时，可得 $RD_2((e+D_{Z_q,\sigma})^m||D_{Z_q,\sigma}^m)=poly(\lambda)$ 。这其中的数学计算就暂时省掉了，密码学总是有许多的数学计算。。。。。