图的概念及存储结构

news2024/11/15 6:16:26

文章目录

    • 图的概念
        • 图(graph)
        • 有向图(directed graph)
        • 无向图(undirected graph)
        • 加权图(weighted graph)
        • 无向完全图(undirected complete graph)
        • 有向完全图(directed complete graph)
        • 子图(subgraph)
        • 稀疏图与稠密图
        • 度
        • 路径与回路
        • 连通图与连通分量
        • 强连通图与强连通分量
        • 生成树
    • 图的存储结构
      • 1.邻接矩阵
        • 1.1概念
        • 1.2结构
        • 1.3 操作
          • 添加顶点AddVertex
          • 添加边弧AddEdge
          • 删除顶点DelVertex
          • 删除边弧DelEdge
        • 1.4特点
      • 2.邻接表
        • 2.1概念
        • 2.2结构
        • 2.3操作
          • 添加顶点AddVertex
          • 添加边弧AddEdge
          • 删除顶点DelVertex
          • 删除边弧DelEdge
        • 2.4特点
    • 源代码

图的概念

图(graph)

是由顶点的非空集合V和边或者弧的集合E组成的, 表示为G=(V,E). 以后将用V(G)和E(G)分别表示图G的顶点集合与边/弧集合.

有向图(directed graph)

若图中顶点对是有序的, 即边是有方向的,边集E(G)为有向边的集合, 则图G称为有向图. 一般将边称为弧(arc), 以有序对<u,v>表示一条从顶点u出发到达顶点v的弧, 其中: u称为弧尾或者起点, v称为弧头或者终点. 在有向图中, <u,v>和<v,u>是不一样的.

无向图(undirected graph)

若图中顶点对是无序的, 即边是无方向的, 边集E(G)为无向边的集合, 则图G称为无向图. 以无序对(u,v)表示u和v之间存在一条无向边. 在无向边中边是对称的, (u,v)和(v,u)表示同一条边.

image-20221230204835546

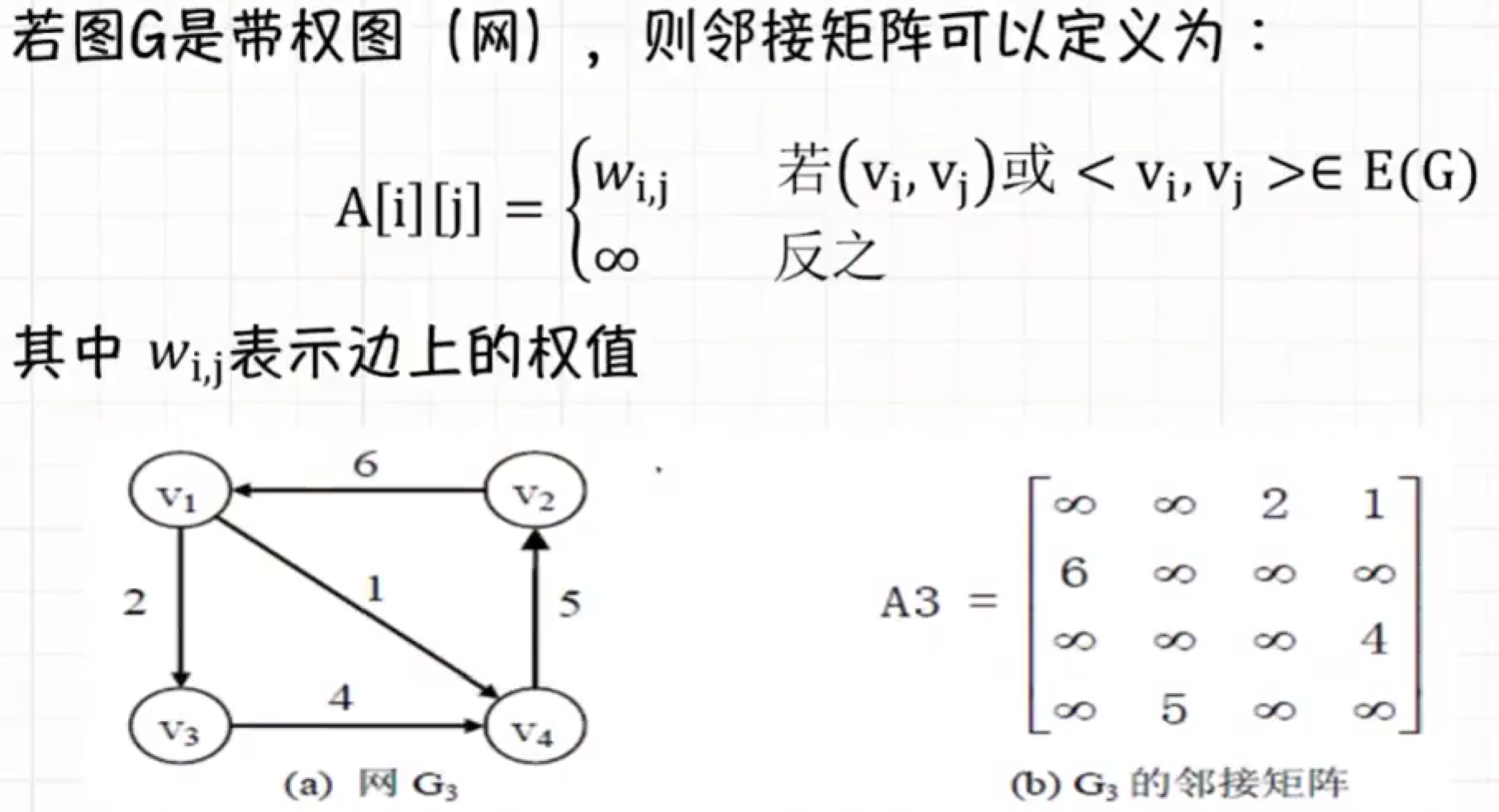
加权图(weighted graph)

边/弧被赋予一个权值的图称为加权图. 如果图是有向的, 称为加权有向图, 如果是无向的, 称为加权无向图.

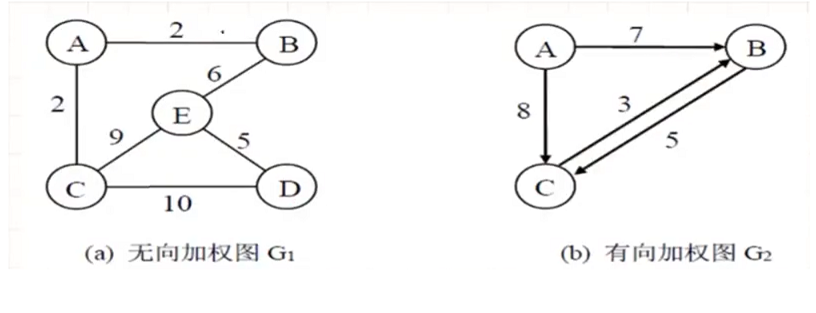
image-20221230204851586

无向完全图(undirected complete graph)

在一个无向图中, 如果任意两个顶点都有一条边直接相连, 则称该图为无向完全图. 具有n个顶点的无向图,边的条数范围为[0, n(n-1)/2]. 无向完全图具有n(n-1)/2条边.

有向完全图(directed complete graph)

在一个有向图中, 如果任意一个顶点都有一条弧直接到达其他顶点, 则称该图为有向完全图. 具有n个顶点的有向图, 弧的条数范围[0, n(n-1)]. 有向完全图具有n(n-1)条弧.

image-20221231183030136

子图(subgraph)

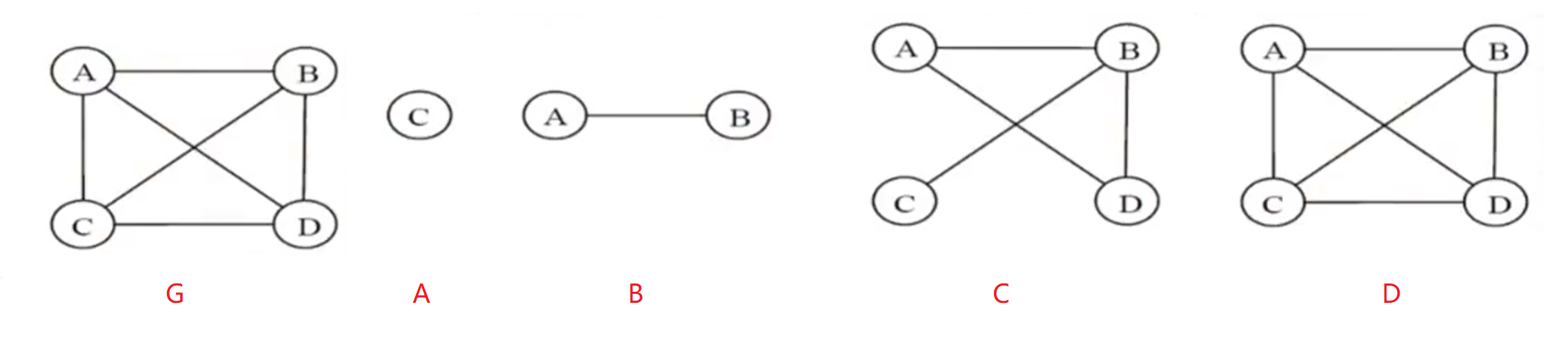
设有两个图G和G~, 且满足条件V(G~)是V(G)的子集, V(G~)⊆V(G), 且E(G~)是E(G)的子集, E(G~)⊆E(G), 则称G~是G的子图.

  • A,B,C,D都是G的子图.

image-20221230211210880

稀疏图与稠密图

有很少的边或者弧的图称为稀疏图, 反之称为稠密图.

度

图G中, 与顶点v相关联的边的数目, 称为顶点v的度. 有向图中顶点v的度是其入度和出度之和.

  • 入度: 有向图中进入某一顶点的边数, 称为该顶点的入度.
  • 出度: 有向图中离开某一顶点的边数, 称为该顶点的出度.
  • 图中顶点的度数之和是边数的两倍.

路径与回路

  • 路径(path): 在无向图G中, 若存在一个从顶点v1到vn的顶点序列v1,v2,…vn满足(vi,vi+1)∈E(1<=i<n), 则称从顶点v1到顶点vn存在一条路径.

  • 路径长度(path length): 是指该路径上经过边或者弧的数目. 对于加权图, 路径长度是指该路径中各边权值之和.

  • 回路/环(cycle): 若一条路径上的第一个顶点和最后一个顶点相同, 则该路径称为回路或者环.

  • 简单路径: 若一条路径上所有的顶点均不重复, 则该路径称为简单路径.

  • 简单回路/环: 除第一个顶点与最后一个顶点之外, 其余顶点均不重复出现的回路, 称为简单回路或者简单环.

连通图与连通分量

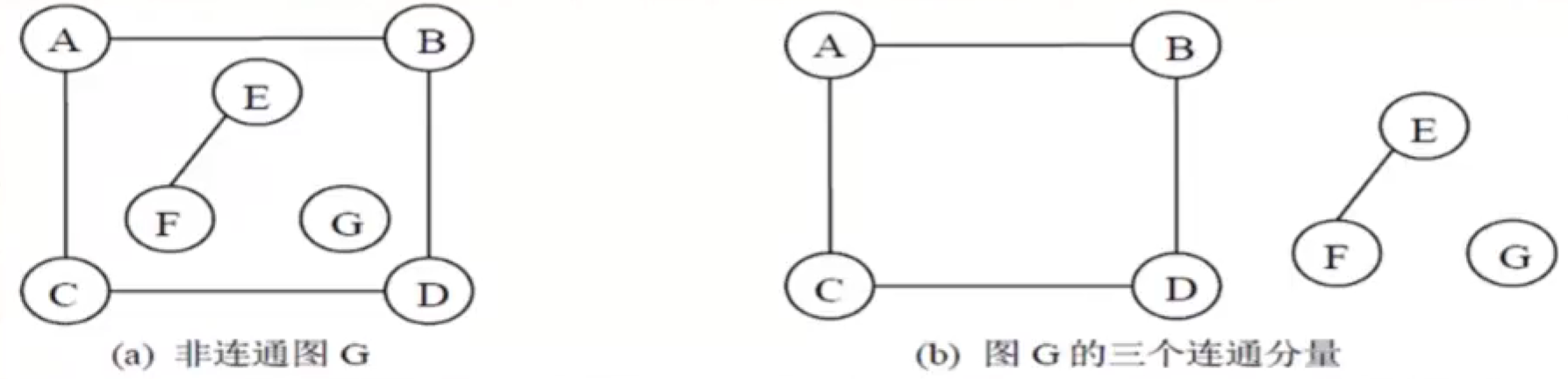
连通图: 在无向图G中, 若从u到v(u!=v)存在路径, 则称u到v是连通的. 若V(G)中的每一对不同顶点u和v都连通, 则称G是连通图.

连通分量: 无向图G中的极大连通子图称为图G的连通分量.

image-20221231143914439

强连通图与强连通分量

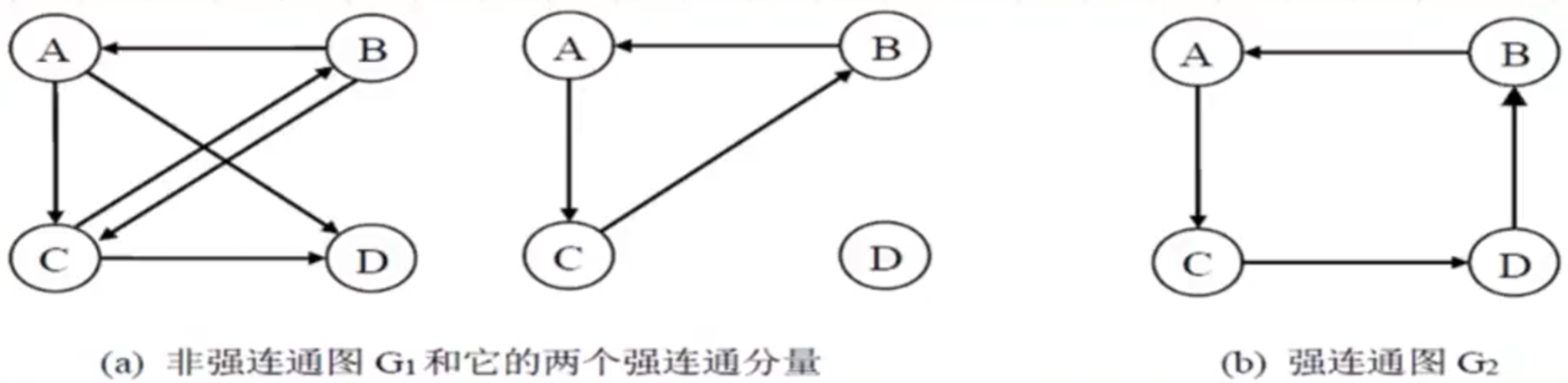
强连通图: 在有向图G中, 若对于V(G)中的每一对不同的顶点u v, 都存在从u到v及v到u的路径, 则称该G是强连通图.

强连通分量: 有向图G中极大强连通子图称为图G的强连通分量.

image-20221231144349627

生成树

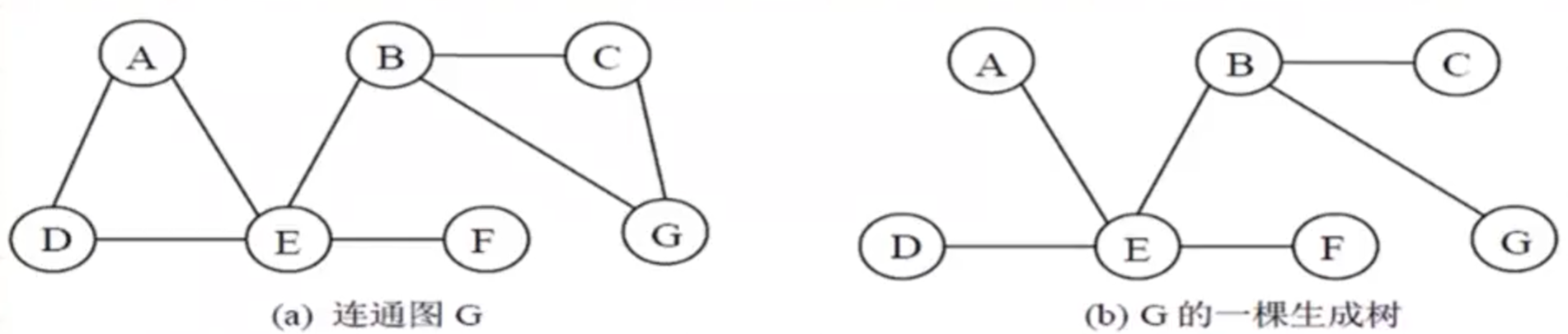
生成树: 是连通图的极小连通子图, 它含有图中全部n个顶点, 但只有足以构成一棵树的n-1条边. 在生成树中再添加一条边之后, 必然会形成回路/环.

  • 生成树不唯一.

image-20221231144706629

图的存储结构

1.邻接矩阵

1.1概念

image-20221231145046826

  • 无向图:
  1. 无向图的邻接矩阵一定是对称矩阵, 因此无向图可以压缩存储.
  2. 第i行(或者第i列)非零元素个数, 表示顶点vi的度.

image-20221231145646314

  • 有向图:
  1. 有向图的邻接矩阵不一定是对称的.
  2. 第i行非零元素个数, 表示顶点vi的出度.
  3. 第i列非零元素的个数, 表示顶点vi的入度.

image-20221231150001123

  • 加权图

image-20221231150218019

1.2结构

  • _vertexSet : 存储顶点,下标找顶点.
  • _vertexIndex : 顶点与下标的映射, 顶点找下标.

如果获取某顶点在邻接矩阵的下标？？？

  1. 将存储顶点的一维数组遍历一遍: 时间复杂度O(n).
  2. 将顶点和对应的下标存储在红黑树(平衡二叉树)中: 时间复杂度O(log2n).
  3. 将顶点和对应的下标存储在哈希表中: 时间复杂度O(1).

使用第一种方案时间效率低下，使用第三种方案虽然时间效率很高，但是所需空间过大，因为我们采用的邻接矩阵的空间开销已经很大了，所以选择采用第二种方案来进行获取某顶点在邻接矩阵的下标。

  • _matrix : 邻接矩阵, 顶点之间的权值.
namespace AdjacentMatrix
{
    // V:顶点类型 W:权值类型 W_MAX:表示不相连 Directed:无向图与有向图的标识 
	template<typename V,typename W,W W_MAX,bool Directed=false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
    }
}

1.3 操作

添加顶点AddVertex
		bool AddVertex(const V& v)
		{
			// 顶点存在不需要继续增加
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);
			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));
			
			// 先在原有的行上一列
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].push_back(W_MAX);
			}

			// 增加一行
			_matrix.push_back(std::vector<W>(_vertexSet.size(), W_MAX));

			return true;
		}
添加边弧AddEdge
		bool AddEdge(const V& src, const V& dst,const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			_matrix[srci][dsti] = weight;

			// 如果为无向图,则需要再添加一条dst->src的边
			if (!Directed)
			{
				_matrix[dsti][srci] = weight;
			}

			return true;
		}
删除顶点DelVertex
		bool DelVertex(const V& v)
		{
			int vi = GetVertexIndex(v);

			// 顶点不在图中,无需删除
			if (vi == -1)
				return false;

			auto pos = std::find(_vertexSet.begin() + vi, _vertexSet.end(), v);
			if (pos != _vertexSet.end())
			{
				_vertexSet.erase(pos);
			}
			else
			{
				return false;
			}

			// 删除该顶点在矩阵中对应的行
			auto ret = std::find(_matrix.begin()+vi, _matrix.end(), _matrix[vi]);
			if (ret != _matrix.end())
			{
				_matrix.erase(ret);
			}
			else
			{
				return false;
			}

			// 删除该顶点在矩阵中对应的列
			for (int i = 0; i < _matrix.size(); i++)
			{
				auto it= std::find(_matrix[i].begin() + vi, _matrix[i].end(), _matrix[i][vi]);
				if (it != _matrix[i].end())
				{
					_matrix[i].erase(it);
				}
				else
				{
					return false;
				}
			}

			// 顶点与下标的关系需要重新映射
			std::map<V, int> tree;

			for (int i = 0; i < _vertexSet.size(); i++)
			{
				tree.emplace(_vertexSet[i], i);
			}

			_vertexIndex.swap(tree);

			return true;
		}
删除边弧DelEdge
		bool DelEdge(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,删除边失败
			if (srci == -1 || dsti == -1)
				return false;

			_matrix[srci][dsti] = W_MAX;
			if (!Directed)
			{
				_matrix[dsti][srci] = W_MAX;
			}
			
			return true;
		}

1.4特点

  1. 图的邻接矩阵表示是唯一的.
  2. 含有n个顶点的图, 其邻接矩阵的空间代价都是O(n2), 与图的顶点数相关, 与边数无关.
  3. 优点: 判断任意两点之间是否有边仅消耗O(1)时间.
  4. 缺点: 即使图中的边数很少, 也需O(n2)空间复杂度, 占用空间太大, 存取数据耗费O(n2)的时间, 消耗时间太久.

2.邻接表

2.1概念

  • 邻接表: 是将图的顶点的顺序存储结构和各顶点的邻接点的链式存储结构相结合的存储方式.
  • 边表: 在邻接表表示法中, 为图中每一个顶点建立一个单链表, 每一个单链表上附设一个头结点.
  • 顶点表: 每一个链表设立一个头结点, 头结点有两个域, 数据域vertex存储顶点信息, 指针域firstEdge则指向顶点vi的第一个邻接点.

image-20221231153652505

	template<typename W>
	struct EdgeNode
	{
		EdgeNode<W>* _next;
		int _to;
		W _weight;

		EdgeNode(int to,const W& weight)
			:_next(nullptr)
			,_to(to)
			,_weight(weight)
		{}
	};

	template<typename V,typename W>
	struct VertexNode
	{
		V _vertex;
		EdgeNode<W>* _firstEdge;

		VertexNode(const V& vertex)
			:_vertex(vertex)
			,_firstEdge(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
	private:
		std::vector<VertexNode<V,W>> _table;
		std::unordered_map<V, int> _vertexIndex;
	};
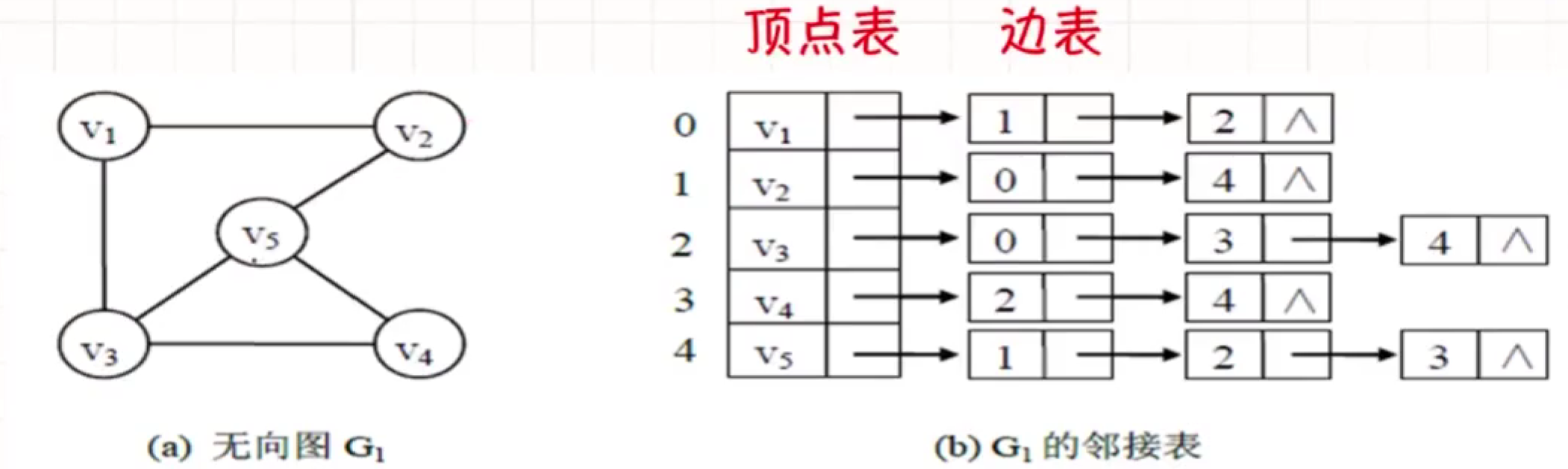
  1. 无向图

对于无向图, 第i个顶点的度为第i个链表的结点数.

image-20221231155249583

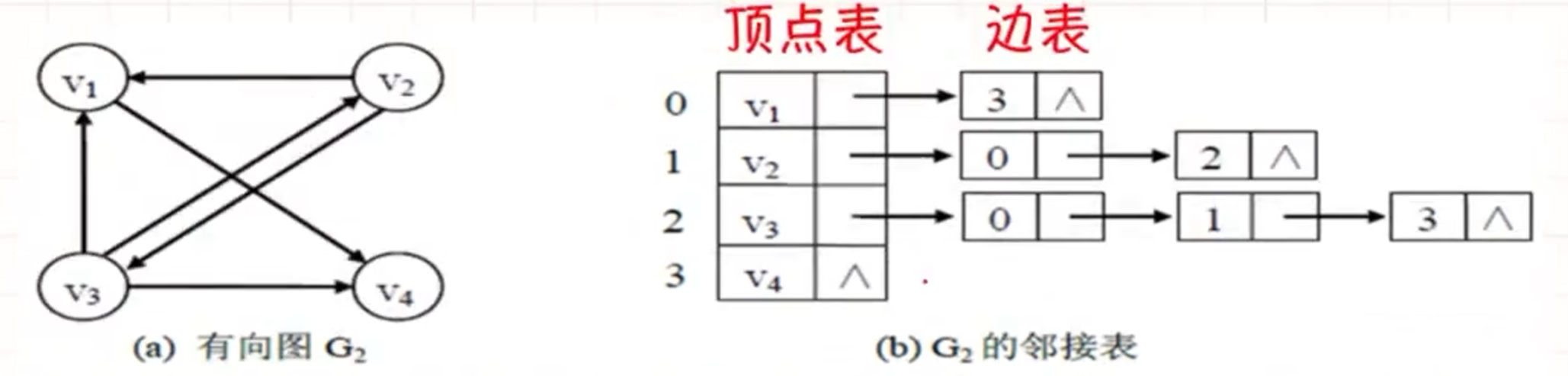
对于有向图, 第i个顶点的出度是第i个链表的结点数, 求第i个顶点的入度需要遍历整个邻接表.

image-20221231155514118

2.2结构

  • _vertexSet : 存储顶点.
  • _vertexIndex : 顶点与下标的映射关系.
  • _table : 出度顶点表.
  • Edge : 相连的顶点边.
namespace AdjacentList
{
	template<typename W>
	struct Edge
	{	
		int _dsti; // 终点顶点的下标
		W _weight; // 边的权值

		struct Edge<W>* _next; // 下一个结点的指针

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			,_weight(weight)
			,_next(nullptr)
		{}
	};

	template<typename V, typename W,bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度顶点表
    }
}

2.3操作

添加顶点AddVertex
  1. 顶点已经在图中, 无需再添加.
  2. 将顶点v直接加入到_vertexSet中.
  3. 再将该顶点与该顶点对应的下标加入到_vertexIndex.
  4. _table也相应加入.
		bool AddVertex(const V& v)
		{
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);

			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			_table.push_back(nullptr);

			return true;
		}
添加边弧AddEdge
		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			Edge* edge = new Edge(dsti, weight);

			// 头插
			edge->_next = _table[srci];
			_table[srci] = edge;

			// 无向图
			if (!Directed)
			{
				edge = new Edge(srci, weight);

				edge->_next = _table[dsti];
				_table[dsti] = edge;
			}

			return true;
		}
删除顶点DelVertex
		bool DelVertex(const V& v)
		{
			int vi = GetVertexIndex(v);

			// 顶点不在图中,无需删除
			if (vi == -1)
				return false;

			// 将所有与v顶点有关的边删除
			for (int i = 0; i < _vertexSet.size(); i++)
			{
				DelEdge(_vertexSet[vi], _vertexSet[i]);
			}

			auto pos = std::find(_vertexSet.begin(), _vertexSet.end(), v);
			if (pos == _vertexSet.end())
			{
				return false;
			}
			_vertexSet.erase(pos);
 
			auto ret = std::find(_table.begin()+vi, _table.end(), nullptr);
			if (ret == _table.end())
			{
				return false;
			}
			_table.erase(ret);

			// 顶点与下标的关系需要重新映射
			std::map<V, int> tree;

			for (int i = 0; i < _vertexSet.size(); i++)
			{
				tree.emplace(_vertexSet[i], i);
			}

			_vertexIndex.swap(tree);

			return true;
		}
删除边弧DelEdge
		bool DelEdge(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,删除边失败
			if (srci == -1 || dsti == -1)
				return false;
			// 与单链表的删除相似
			Edge* prev = nullptr;
			Edge* curr = _table[srci];
			
			while (curr != nullptr)
			{
				if (curr->_dsti == dsti)
				{
					if (prev == nullptr)
					{
						_table[srci] = curr->_next;
					}
					else
					{
						prev->_next = curr->_next;
					}
					delete curr;
					break;
				}
				prev = curr;
				curr = curr->_next;
			}

			if (!Directed)
			{
				prev = nullptr;
				curr = _table[dsti];

				while (curr != nullptr)
				{
					if (curr->_dsti == srci)
					{
						if (prev == nullptr)
						{
							_table[dsti] = curr->_next;
						}
						else
						{
							prev->_next = curr->_next;
						}
						delete curr;
						break;
					}

					prev = curr;
					curr = curr->_next;
				}
			}
			return true;
		}

2.4特点

邻接表是图的标准存储方方式, 图的邻接表表示不唯一.

优点: 空间=顶点数+边弧数, 处理时间也是顶点数+边弧数, 即为O(V+E). 在边稀疏的情况下, 用邻接表存储图比用邻接矩阵存储图更节约空间.

缺点: 确定u 与 v 是否有边, 最坏消耗O(n)时间. 无向图同一条边会表示两次, 有向图中寻找某顶点的入度边, 比较费时间.

源代码

[源码地址](three20221229/three20221229 · yx_零叁/C与C++ - 码云 - 开源中国 (gitee.com))

image-20221231161753273

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/131050.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

STM32H750自制开发板调试经验

STM32H750自制开发板调试经验

​本篇只是一个记录&#xff0c;没啥可看的。 STM32H750硬件相关 STM32H750可以通过USB-OTG下载程序&#xff0c;也可以使用SWD进行调试&#xff0c;所以设计板子得时候将PA13和PA12预留出来即可&#xff0c;后续也可以用作usb虚拟串口&#xff08;CDC&#xff09;功能或者模拟…
阅读更多...
stm32f407VET6 系统学习 day08 利用adc 模数转换 监控光敏电阻。

stm32f407VET6 系统学习 day08 利用adc 模数转换 监控光敏电阻。

1. ADC 的知识 1.基本概念 &#xff1a; Analog-to-Digital Converter的缩写。指模/数转换器或者模拟/数字转换器。是指将连续变量的模拟信号转换为离散的数字信号的器件 。典型的模拟数字转换器将模拟信号转换为表示一定比例电压值的数字信号。 2.STM32F4x ADC特点 1. 可配…
阅读更多...
git操作

git操作

删除暂存区文件&#xff1a; git rm --cached 完整文件名 git rm --cached xxx.txt这个删&#xff0c;只是把暂存区里的文件删了&#xff0c;工作区里面的没有删 把本地文件添加到暂存区 git add完整文件名 例如&#xff1a;git add xxx.txt git add xxx.txt此时xxx.txt已经…
阅读更多...
Linux 权限理解和学习

Linux 权限理解和学习

✨个人主页&#xff1a; Yohifo &#x1f389;所属专栏&#xff1a; Linux学习之旅 &#x1f38a;每篇一句&#xff1a; 图片来源 &#x1f383;操作环境&#xff1a; CentOS 7.6 阿里云远程服务器 Don’t argue with the people of strong determination, because they may ch…
阅读更多...
AtCoder Beginner Contest 283 Ex. Popcount Sum（类欧经典问题：数x在二进制表示下第k位的值）

AtCoder Beginner Contest 283 Ex. Popcount Sum（类欧经典问题：数x在二进制表示下第k位的值）

题目 t(t<1e5)组样例&#xff0c;每组样例给定n,m,r(1<m<n<1e9,0<r<m) 求[1,n]这n个数中&#xff0c;所有满足i%mr的数i的二进制的1的个数之和 即&#xff1a;&#xff0c; 其中&#xff0c;__builtin_popcount(i)统计的是i的二进制表示中&#xff0c;1的…
阅读更多...
Web APIs

Web APIs

文章目录一. Web API介绍1. Web APIs 和 JS 基础关联性1.1 JS 的组成1.2 JS 基础阶段以及 Web APIs 阶段2. API的概念[3.Web API的概念](https://developer.mozilla.org/zh-CN/docs/Web/API)4. API 和 Web API 总结二. DOM 介绍1. DOM 简介1.1 什么是 DOM1.2 DOM 树2. 获取元素…
阅读更多...
Linux-6 三剑客命令

Linux-6 三剑客命令

Linux-6 三剑客命令 awk&#xff08;取列&#xff09; 将系统的IP地址打印出来 [rootdestiny ~]# yum install net-tools -y #分析&#xff1a;#1.肯定是需要拿到IP地址&#xff0c;仅看某一个特定的网卡&#xff1b;ifconfig#2.先想办法过滤出数据的那一行&#xff1b; ###行#…
阅读更多...
5）Django Admin管理工具，Form组件，Auth

5）Django Admin管理工具，Form组件，Auth

目录 一 Django Admin管理工具 激活管理工具 使用管理工具 复杂模型 自定义表单 内联(Inline)显示 列表页的显示 二 django Form组件 局部钩子和全局钩子 三 Django 用户认证&#xff08;Auth&#xff09;组件 一 Django Admin管理工具 Django 提供了基于 web 的管理…
阅读更多...
年终报告撰写小技巧，你学会了吗？

年终报告撰写小技巧，你学会了吗？

年年岁岁花相似&#xff0c;岁岁年年人不同。 临近年底&#xff0c;又到了一年一度的年终报告时段了。同事间见面最让人头疼的问候&#xff0c;莫过于&#xff0c;“你的年终报告写了吗&#xff1f;” 有的人东拼西凑、应付了事&#xff0c;汇报内容乏善可陈&#xff0c;领导…
阅读更多...
美美的圣诞树画出来-CoCube

美美的圣诞树画出来-CoCube

2022年圣诞节到来啦&#xff0c;很高兴这次我们又能一起度过~ CSDN诚邀各位技术er分享关于圣诞节的各种技术创意&#xff0c;展现你与众不同的精彩&#xff01;参与本次投稿即可获得【话题达人】勋章【圣诞快乐】定制勋章&#xff08;1年1次&#xff0c;错过要等下一年喔&#…
阅读更多...
尚医通-上传医院接口实现（十八）

尚医通-上传医院接口实现（十八）

目录&#xff1a; &#xff08;1&#xff09;上传医院接口-基础类的创建 &#xff08;2&#xff09;数据接口-上传医院接口-初步实现 &#xff08;3&#xff09;上传医院接口-最终实现 &#xff08;1&#xff09;上传医院接口-基础类的创建 复制相关的工具类&#xff1a;这…
阅读更多...
Redis Windows版安装和使用

Redis Windows版安装和使用

下载地址&#xff0c;亲已测试可放心使用 https://github.com/tporadowski/redis/releases Redis安装和基本使用&#xff08;windows版&#xff09; 1.Redis简介 完全开源免费的高性能的key-value的数据库 支持数据的持久化&#xff0c;可以将内存中的数据保存在磁盘中&…
阅读更多...
【函数】一篇文章带你看懂控制流、递归、高阶函数

【函数】一篇文章带你看懂控制流、递归、高阶函数

目录 控制流 条件语句 迭代语句 示例&#xff1a;质因数分解 递归 示例&#xff1a;阶乘 示例&#xff1a;斐波那契数列 示例&#xff1a;判断奇偶数 高阶函数 lambda 表达式 设计函数 示例&#xff1a;累加计算 示例&#xff1a;柯里化 Lab 1: Functions, Control …
阅读更多...
个人能用的短信平台有哪些？看这一篇就够了

个人能用的短信平台有哪些？看这一篇就够了

对于程序员个人来说&#xff0c;在做开发或者是接项目的时候&#xff0c;常常会用到发送短信功能模块&#xff0c;而自己写这个模块会要相当多的精力和时间&#xff0c;去找短信平台来解决问题&#xff0c;已经成了不少程序员的共识。 但市面上的短信平台确实很杂&#xff0c;鱼…
阅读更多...
服务注册与发现原理

服务注册与发现原理

一、什么是服务注册与发现&#xff1f; 服务注册与发现就是一套管理微服务的组件&#xff0c;方便各拆分的服务平滑上线和下线&#xff0c;以及某个服务出现故障自动剔除。其实质就是维护一张记录各在线服务的表。让消费服知道服务在线可以请求。。。。。。 二、服务注册与发现…
阅读更多...
SQL限制

SQL限制

SQL限制目录概述需求&#xff1a;设计思路实现思路分析1.URL管理参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,full busy&#xff0c;skip hardness,make a better result,wait for change,challenge Survive. happy…
阅读更多...
PLL实验

PLL实验

PLL实验 开发板上面只有一个200MHz时钟输入&#xff0c;对于其它频率的时钟怎么办&#xff1f; 介绍 其实在很多 FPGA 芯片内部都集成了 PLL &#xff0c;其他厂商可能不叫 PLL &#xff0c;但是也有类似的功能模块&#xff0c;通过 PLL 可以倍频分频&#xff0c;产生其他很…
阅读更多...
pytorch搭建yolov3网络

pytorch搭建yolov3网络

yolov3的整体网络结构 主要包含了两个部分。左边的Darknet-53主干特征提取网络主要用于提取特征。右边是一个FPN金字塔结构。 主干特征提取网络&#xff08;提取特征&#xff09; import math from collections import OrderedDict import torch.nn as nn#------------------…
阅读更多...
MySQL事务相关知识

MySQL事务相关知识

实践阅读&#xff1a;一文彻底读懂MySQL事务的四大隔离级别 1、什么是事务&#xff1f; 数据库事务&#xff08;简称&#xff1a;事务&#xff09;&#xff0c;是数据库管理系统执行过程中的一个逻辑单位&#xff0c;由一个有限的数据库操作序列构成&#xff0c;这些操作要么全…
阅读更多...
AcWing 4645. 选数异或(预处理小区间 + 二分优化找)

AcWing 4645. 选数异或(预处理小区间 + 二分优化找)

题目如下&#xff1a; 题解 or 思路 在 [l,r][l, r][l,r] 区间内找到两个数 a,ba, ba,b 使得 a ^ b x 通过异或的性质&#xff1a; a ^ b ^ b x ^ b > a x ^ b 我们可以通过 b 可以迅速找到 a, a x ^ b 我们可以现预处理出所有小区间(大区间可以不需要&#xff0c;因为…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023