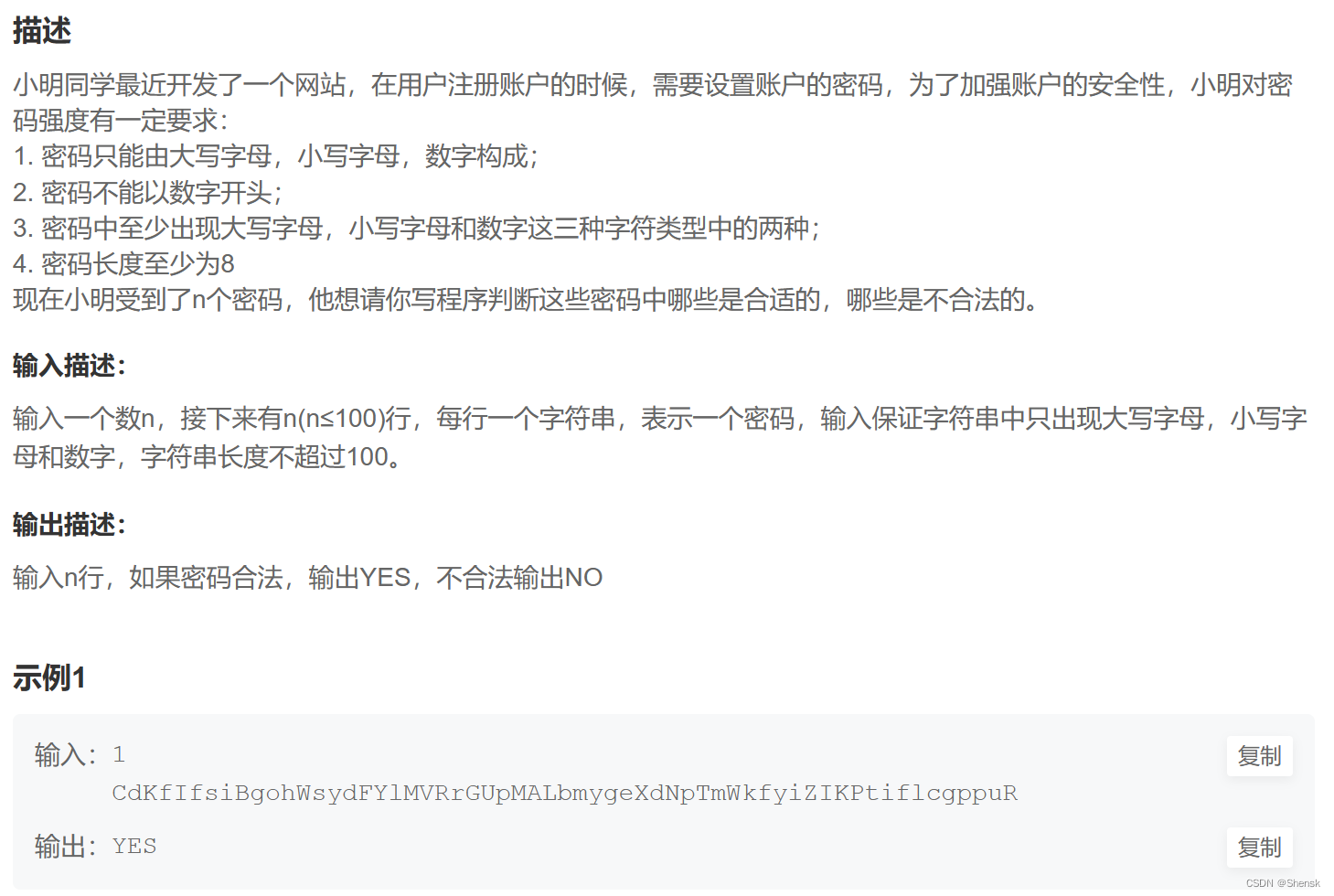
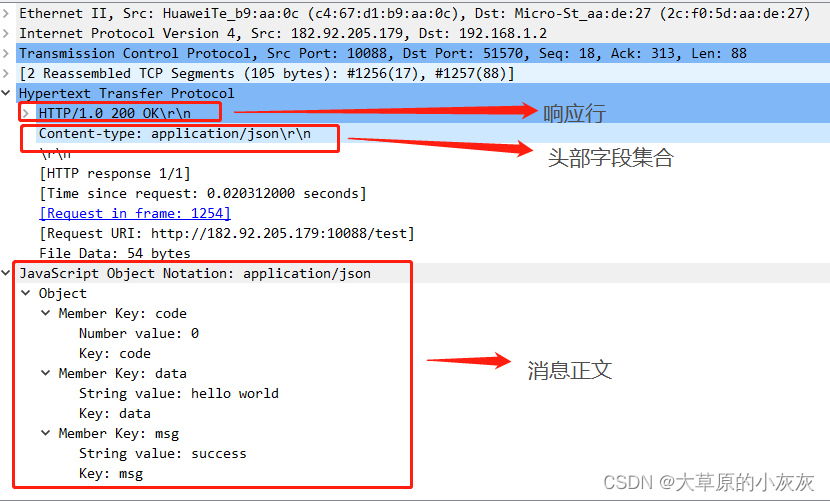
题目如下：

题解 or 思路

在 $[l,r]$ 区间内找到两个数 $a,b$ 使得 a ^ b = x
通过异或的性质： a ^ b ^ b = x ^ b => a = x ^ b
我们可以通过 b 可以迅速找到 a, a = x ^ b
我们可以现预处理出所有小区间(大区间可以不需要，因为小区间一定在大区间里面 如：[1, 4], [1, 3], 我们 只需要记录[1, 3]即可)
按左区间第一排序准则，右区间第二排序准则，进行从小到大的区间排序
通过二分我们可以迅速找到 满足的左区间，逐一 $check$ 一下， 如果左区间 大于等于 找的右区间，就可以 $break$ 了。

AC 代码如下：

const int N = 2000009;
int n, m, x, s[N];
vector<PII> can;
vector<int> v[N];
void solve()
{
    cin >> n >> m >> x;
    for (int i = 1; i <= n; i++)
        cin >> s[i];
    for (int i = 1; i <= n; i++)
    {
        if (v[x ^ s[i]].size())
        {
            can.push_back({ v[x ^ s[i]][v[x ^ s[i]].size() - 1], i });
        }
        v[s[i]].push_back(i);
    }
    auto cmp = [](PII a, PII b)
    {
        if (a.first == b.first)
            return a.second < b.second;
        return a.first < b.first;
    };
    sort(can.begin(), can.end(), cmp);
    while (m--)
    {
        int l, r;   cin >> l >> r;
        int lt = 0, rt = can.size() - 1;
        while (lt < rt)
        {
            int mid = lt + rt >> 1;
            if (can[mid].first >= l)
                rt = mid;
            else
                lt = mid + 1;
        }
        bool flag = 0;
        for (int i = rt; i < can.size(); i++)
        {
            if (can[i].first >= r)
                break;
            if (can[i].first >= l && can[i].second <= r)
            {
                flag = 1;
                cout << "yes\n";
                break;
            }
        }
        if (!flag)
            cout << "no\n";
    }
}
int main()
{
    buff;
    solve();
}
/*
a ^ b = x
check [l, r] 是否存在 x ^ a = b, a, b 在[l, r]里面
*/