题目链接：力扣

 

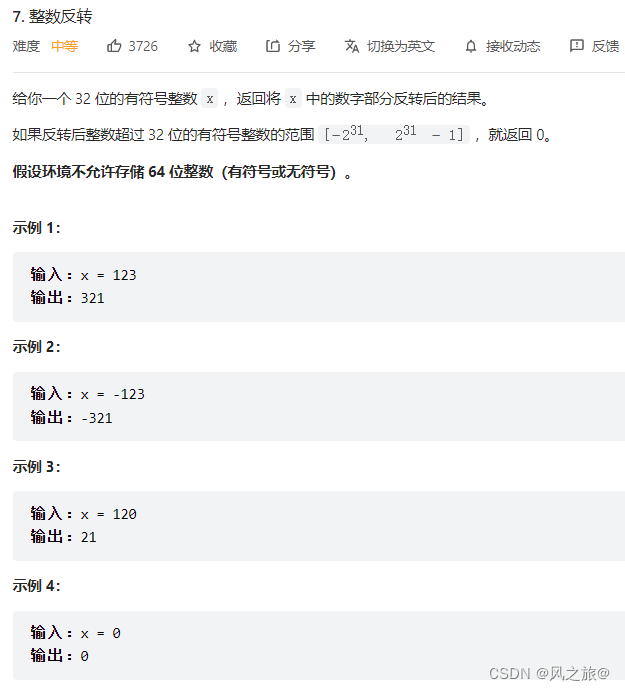
解题思路：

题目要求中有一句话：假设环境不允许存储 64 位整数（有符号或无符号）。 

也就是说不能使用long类型来判断是否int溢出，只能使用int类型进行运算

首先对于一个整数的翻转比较简单：对10进行取模运算，比如数字x= 1234，反转后的新数字result=0：

1234%10 = 4，得到末尾4，然后1234/10=123，result= result*10+4;

123%10 = 3，得到末位3，然后123/10 =12，result= result*10+3;

12%10=2，得到末位2，然后12/10 = 1，result= result*10+2;

1%10=1，得到末尾1，然后1/10=0，result= result*10+1;

x=0，结束

当x为负数时，上述过程也依然成立，对与负数，对10取模得到的余数也是一个负数，result每次加的都是一个负数，最终result的结果就是所求。

但是上述过程可能会发生整数的溢出，比如x=1234567899，翻转后为9987654321，超过了32位有符号数的最大值2147483647，发生了溢出。

有一种比较简单的判断溢出的方式：观察result的更新过程，每一次乘10后，再加上得到的末位数字，所以，可以使用一个额外的变量prev表示上一轮result的值，如果本轮循环result/10的值不等于prev则发生的溢出，这种方式对于正数溢出和负数溢出的判断都适用。如果一个数乘10后发生了溢出，那么显然溢出后的值与原来的值不是10倍的关系。

比如int a = 9876544321，则a*10 = 1286608618，1286608618/10 =128660861，不等于a 显然发生了溢出。

AC代码

class Solution {
    public static int reverse(int x) {
        int result = 0;
        int prev;
        while (x != 0) {
            prev = result;
            result = result * 10 + x % 10;
            if (result / 10 != prev) {
                return 0;
            }
            x /= 10;
        }
        return result;
    }
}