🌈1.Pow(x,n)

 

• -100.0 < x < 100.0
• -2^31 <= n <= 2^31-1
• n 是一个整数
• -10^4 <= x^n <= 10^4

思路分析：

暴力求解直接一个for循环n个x相乘解决，但是你拿那代码怎么好意思拿高薪？

所以而且那个的时间复杂度是O(n),效率并不是很高，我们再学习新的。

• 1.分治实现(快速幂+递归)

x→x^2→x^4→x^8→x^16→x^32→x^64

从 x 开始，每次直接把上一次的结果进行平方，计算 6次就可以得到 x^64 的值，而不需要对 x乘 63次 x。

这个幂是偶数，如果幂是奇数咋办？

例如：x^77:

x→x^2→x^4→x^9→x^19→x^38→x^77

x→x^2,x^2→x^4,x^19→x^38这几步是直接平方处理，其他步是平方处理后再乘x处理。

如果说拆分从左往右不好看出来，那就从右往左倒着看。

这里还要注意一个细节，就是n<0,那样幂是负数，所以把求得的数倒过来变成分之一就行了。

• 首先是实现一个快速幂函数两个形参(底数x,指数N）

1.  如果指数是0，那直接返回0，任何数的0次方是1。
2. 这里我们是根据N逆着推导，设置一个变量y，y就是一个过度，由于我们把总结果看作是一个数的平方，所以把y就看作这个数，如果N是偶数，就是y*y，如果是奇数就要再多乘一个x，y*y*x,在调用递归继续去分解这个y去找y=y1*y1。一直递归到x^0。

class Solution {
public:
    double QuickMul(double x, long long N)
    {
       //x是底数，N是指数
       if(N == 0)  //任何数的0次方为一，除去0
       {
           return 1.0;
       }
       double y = QuickMul(x, N/2);
       return N%2 == 0 ? y*y : y*y*x;
    }
    double myPow(double x, int n) {
        long long N = n;
        return N >= 0 ? QuickMul(x, N) : 1.0 / QuickMul(x, -N);
    }
};

复杂度分析

时间复杂度：O(log n)，即为递归的层数。

空间复杂度：O(log n)，即为递归的层数。这是由于递归的函数调用会使用栈空间。

• 2.快速幂+迭代

我们还是以 x^{77} 作为例子：

x→x^2→x^4→+x^9→+x^19→x^38→+x^77

这个+就是标记一下那一次需要多乘x，没啥特殊含义。

• x^38→+x^77中额外贡献了一个x。
• +x^9→+x^19中额外贡献一个x,但是这个x被平方2次(19到38一次，38到77一次)=x^2^2=x^4
• x^4→+x^9中额外贡献一个x,但是这x被平凡3次，x^2^3=x^8。

• 最初的 xx 在之后被平方了 66 次，因此在 x^77 中贡献了 x^2^6= x^64。

我们把这些贡献相乘x*x^4*x^8*x^64=x^77,恰好等于 x^77 。

• 而这些贡献的指数部分又是什么呢？它们都是 2 的幂次，这是因为每个额外乘的 x 在之后都会被平方若干次。而这些指数 1，4，8 和 64，恰好就对应了 77 的二进制表示 (1001101)_2
• 中的每个 1！
• 因此我们借助整数的二进制拆分，就可以得到迭代计算的方法，一般地，如果整数 nn 的二进制拆分为:n=2^i0​+2^i1​+⋯+2^ik​
• 这样以来，我们从 x 开始不断地进行平方，得到x^2, x^4, x^8, x^16,⋯如果 n 的第 k 个（从右往左，从 0 开始计数，二进制都是从右往左）二进制位为 1，那么我们就将对应的贡献 x^2k。

所以设一个ans为贡献总和，如果N%2==1，那它一定贡献一个x，然后N/2,再判断是否贡献x,就这个一直循环，直到N=1,然后把所有的贡献x累乘即可。

class Solution {
public:
    double QuickMul(double x, long long N) {
        double ans = 1.0;
        // 贡献的初始值为 x
        double x_contribute = x;
        // 在对 N 进行二进制拆分的同时计算答案
        while (N > 0) {
            if (N % 2 == 1) {
                // 如果 N 二进制表示的最低位为 1，那么需要计入贡献
                ans *= x_contribute;
            }
            // 将贡献不断地平方
            x_contribute *= x_contribute;
            // 舍弃 N 二进制表示的最低位，这样我们每次只要判断最低位即可
            N /= 2;
        }
        return ans;
    }

    double myPow(double x, int n) {
        long long N = n;
        return N >= 0 ? QuickMul(x, N) : 1.0 / QuickMul(x, -N);
    }
};

---

---

---

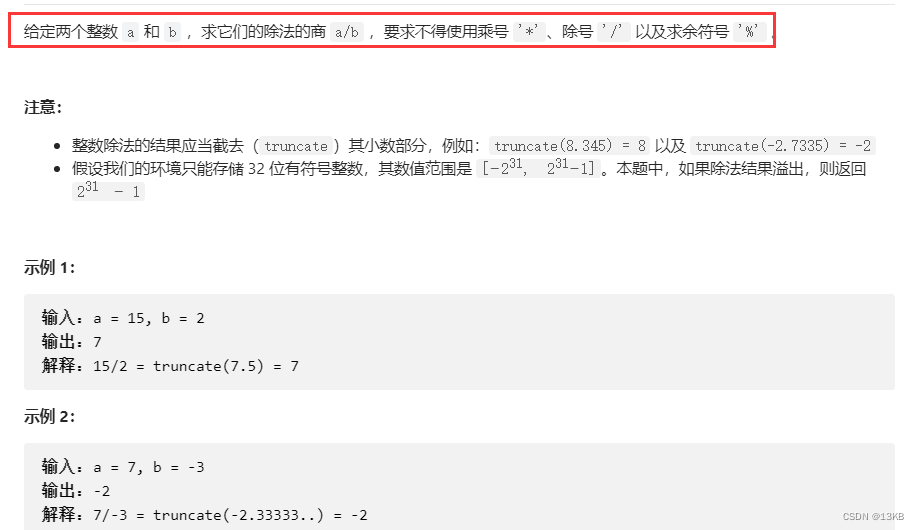
 🌈2.整数除法 

   【简单】

提示:

• -231 <= a, b <= 231 - 1
• b != 0

这就是力扣的简单题型吗？这还指什么offer，直接进场了。

🐎思路分析：

xdm,这个题是考啥的？个人认为是不是对边界判定，溢出和二分查找有联系。

首先我们就要对容易发生溢出或者是易错边界讨论：

• 当被除数a为 32 位有符号整数的最小值 -2^31 时：

1. 如果除数为 1，那么我们可以直接返回答案 -2^31 ；
2. 如果除数为 -1，那么答案为 2^31，产生了溢出。此时我们需要返回 2^31  −1。

• 当除数b为 32位有符号整数的最小值 -2^31时：

1. 如果被除数同样为 -2^31，那么我们可以直接返回答案 1；
2. 对于其余的情况，我们返回答案 0。

• 当被除数a为0时,我们可以直接返回答案0。

其次我们就要讨论这两个数相除的4中符号形式:(正正，正负，负正，负负）

• 那肯定第一反应就是符号变成相同的，所以都变成正的，最后再变回来。但是如果说被除数是-2^31，那他的正数就是2^31，越界了(题上的注意)。
• 所以把他俩都变成负数这样就不需要考虑越界和溢出问题了。
• 最后返回的时候别忘了变回来。

class Solution {
public:
    int divide(int a, int b) {
        //如果被除数是32位最小值
        if(a==INT_MINT)
        {
            if(b==1)
              return INT_MINT;
            if(b==-1)
                return INT_MAX;
        }
        //如果除数是最小值
        if(b==INT_MINT)
        {
            if(a==INT_MINT)
                return 1;
            else
             return 0;
        }
        //被除数为0，(除数不能为0)
        if(a==0)
        {
            return 0;
        }
    }
};

准备工作已经做好，接下来进行二分查找。

老师说一定要做足前戏，不能直奔主题，现在前戏已经完成，接下来就该高潮部分了。

接下来我们设商是c,a/b=c所以c不是正数就是0，这是前提条件。

我们把a,b,c都看成是正数，a>=b*c(9/2=4,9>2*4)，但是a,b都是负数，所以a<=b*c

• 所以这个题我们利用二分查找找出最大的数c使得b*c>=a成立就行了。

1. 不出意外的话就出现了意外，这个题不让使用‘*’

2. 二分查找的下界为 1，上界为 2^31 - 1。唯一可能出现的答案为 2^31的情况已经被我们在前言部分进行了特殊处理，因此答案的最大值为 2^31 - 1。如果二分查找失败，那么答案一定为 0。

3. 所以我们就会使用到快速乘，和上面的快速幂很相似，前者通过加法实现乘法，后者通过乘法实现幂运算。
4. 在实现「快速乘」时，我们需要使用加法运算，然而较大的 c 也会导致加法运算溢出。例如我们要判断 a + b是否小于 c 时（其中 a, b, c均为负数），a+b可能会产生溢出，因此我们必须将判断改为 a<c-b是否成立。由于任意两个负数的差一定在 [-2^{31} + 1, 2 ^31-1] 范围内，这样就不会产生溢出。
5. 我们需要使用「快速乘」算法得到Z×Y 的值。然后再去找最大的Z。

class Solution {
public:
    int divide(int a, int b) {
        // 考虑被除数为最小值的情况
        if (a == INT_MIN) {
            if (b == 1) {
                return INT_MIN;
            }
            if (b == -1) {
                return INT_MAX;
            }
        }
        // 考虑除数为最小值的情况
        if (b == INT_MIN) {
            return a == INT_MIN ? 1 : 0;
        }
        // 考虑被除数为 0 的情况
        if (a == 0) {
            return 0;
        }
        
        // 一般情况，使用二分查找
        // 将所有的正数取相反数，这样就只需要考虑一种情况
        bool rev = false;
        if (a > 0) {
            a = -a;
            rev = !rev;
        }
        if (b > 0) {
            b = -b;
            rev = !rev;
        }

        // 快速乘
        auto quickAdd = [](int y, int z, int x) {
            // x 和 y 是负数，z 是正数
            // 需要判断 z * y >= x 是否成立
            int result = 0, add = y;
            while (z) {
                if (z & 1) {
                    // 需要保证 result + add >= x
                    if (result < x - add) {
                        return false;
                    }
                    result += add;
                }
                if (z != 1) {
                    // 需要保证 add + add >= x
                    if (add < x - add) {
                        return false;
                    }
                    add += add;
                }
                // 不能使用除法
                z >>= 1;
            }
            return true;
        };
        
        int left = 1, right = INT_MAX, ans = 0;
        while (left <= right) {
            // 注意溢出，并且不能使用除法
            int mid = left + ((right - left) >> 1);
            bool check = quickAdd(b, mid, a);
            if (check) {
                ans = mid;
                // 注意溢出
                if (mid == INT_MAX) {
                    break;
                }
                left = mid + 1;
            }
            else {
                right = mid - 1;
            }
        }

        return rev ? -ans : ans;
    }
};

result + add >= x这个咋一看有点难理解，但是因为都是负数，所以反过来看就是如果当前值已经比x（实际值）大则退出了，即已经不满足z*y<x（正数情况）。

这要是简单题那不废了。