子节点优化选择策略
(1)子节点选择方式
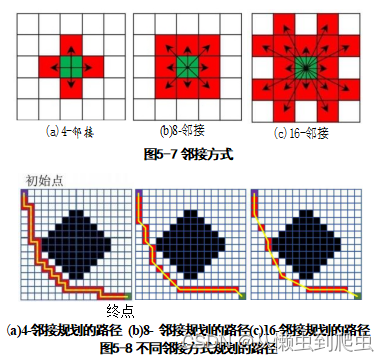
为了找到从起始点到终点的路径,需定义一种可以选择后续节点的方式。在 A*算法中两种常见的方法为4-邻接(见图5-7(a) 和8-邻接(见图5-7(b)), 但考虑到 在复杂越野环境上,我们希望智能车辆允许更多的自由运动来更好规避危险,因此
本文选择16-邻接(见图5-7(c))。
如图5-8所示,4-邻接规划的路径具有很多的直角拐点且路径最长,其次是8- 邻接规划的路径,而16-邻接规划的路径平滑、拐点数少、路径短,适合复杂越野
环境智能车的需求。
在越野栅格地图中,我们使用节点之间的距离作为全局评估函数中真实代价 函 数g(n) 的计算成本。规定:上下左右移动成本为1;对角45°移动成本为 √ 2; 其余方向移动成本为 √ 5。考虑到计算机对小数处理速度慢于处理整数,则将成本 扩大10倍,最后上下左右移动成本为10;对角45°移动成本为14;其余方向移动成本为22。
(2)优化子节点选择
传统 A* 算法在子节点选取上,仅考察子节点周围是否为障碍物,而未考察子 节点与障碍物位置的相关性,从而规划出路线存在斜着通过障碍物栅格顶点的问 题,导致车辆可能与障碍物发生碰撞。因为本文中所构建环境模型具有更危险的威
胁物存在,所以优化了子节点的选择规则。如图5-9,为16个子节点分布图。本文结合越野环境栅格地图R, 设计的子节点选择规则为:
1:若子节点4或子节点12具有威胁(在越野环境栅格地图R 中值≥1),则子节 点2、子节点6、子节点3、子节点5或子节点13、子节点9、子节点14、子节点11不作为预选点。
x = m(x) # run
File "/home/xugaoxiang/anaconda3/envs/pytorch1.6/lib/python3.7/site-packages/torch/nn/modules/module.py", line 722, in _call_impl
result = self.forward(*input, **kwargs)
File "/home/xugaoxiang/Works/Yolov5-Deepsort-Fastreid/models/yolo.py", line 36, in forward
self.training |= self.export2: 若子节点16或子节点8具有威胁,则子节点2、子节点13、子节点15、子节点1或子节点6、子节点9、子节点10、子节点7不作为预选点。
#获得任意节点信息 ,__getitem__()魔法函数作用为当实例化对象map进行map[key]操作上自动调用。
def __getitem__(self, item):
return self.data[item]
###############创建点类################
class Point:
#初始化
def __init__(self,x,y):
self.x=x
self.y=y
#判断是否同一个点
def __eq__(self, other):
if self.x==other.x and self.y==other.y:
return True
return False3: 均无具威胁,则不做处理。
优化子节点选择后,规划后的路径避开具有威胁栅格的顶点,避免智能车辆在运动中发生碰撞,更符合实际要求。

5.3.3 自适应评估函数设计
为权衡复杂越野环境下智能车辆的行驶安全与行车效率之间的关系,规划出 安全可行的行车路径,本文提出改进的 A*算法。传统的 A*算法的评价函数一般 为:
f(n)=g(n)+h(n)
(5.14) 式中: f(n) 为全局代价函数, g(n) 为真实代价函数, h(n) 为启发函数。针对传统 A*算法计算效率、无法自适应不同任务要求和拐点数量多等问题,因此,本文算 法提出了方向变化惩罚与局部区域复杂度惩罚来自适应调整g(n) 和h(n) 的比例系数。
(1)方向变化惩罚
在传统的 A* 算法中,计算节点的真实代价函数g(n) 值时,到邻域任何子节点 并没有产生惩罚。然而实际的车辆行驶中,我们希望车辆保持直线行驶,所以规划 的路径应笔直、更少转弯和转弯的角度应小点等,因此本文引入方向变化惩罚,来 减少路径的无用拐点。
在越野环境中,本文规定智能车的转弯角度范围为0°~90°,将方向变化对车辆行驶的影响近似转换为行驶距离的增加,即:在原本的移动成本上进行惩罚。
# 描述AStar算法中的节点数据
class Node:
#初始化
def __init__(self, point, startPoint,endPoint, g=0,w=1,p=1):
self.point = point # 自己的坐标
self.father = None # 父节点
self.g = g # g值,g值在用到的时候会重新算
# 计算h值,采用曼哈顿距离
#self.h = (abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) * 10
#采用欧几里得距离
#self.h = math.pow((math.pow((endPoint.x - point.x),2) + math.pow((endPoint.y - point.y),2)),0.5)*10
#采用对角距离
pp=(1-p)+0.2*math.exp((math.pow((math.pow((endPoint.x - point.x),2) + math.pow((endPoint.y - point.y),2)),0.5))/(math.pow((math.pow((endPoint.x - startPoint.x),2) + math.pow((endPoint.y - startPoint.y),2)),0.5)))
Diagonal_step = min((endPoint.x - point.x),(endPoint.y - point.y))
straight_step = (abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) - 2*Diagonal_step
self.h =(straight_step + math.pow(2,0.5)*Diagonal_step)*10*pp
#print(pp)方向变化惩罚规则为:
Stepl:计算当前节点与该其父节点的方向 Direction1,方向规定如图5-10(a)所 示。
Step2: 计算当前节点到其子节点的方向 Direction2。
Step3: 计算D_Change=|Direction1-Direction2|, 若 D_Change>4, 则将方向变化惩罚 D_P 置为无穷大,若D_Change≤4, 则参考表5.2 选择相应的方向变化惩 罚系数,图5-10(b) 已给出相应的例子参考。
Step4: 计算子节点的真实代价函数值。通过方向变化惩罚后,可以使得规划的路径尽量保持直线,减少拐点,使得路径更加高效、符合实际要求。


(2)局部区域复杂度惩罚
通过方向变化惩罚后,增加了节点的真实代价值,在A*算法中,真实代价G 大于预估代价 H 时,会增加算法的搜索范围,使得效率降低。所以本小节引入了 局部区域复杂度惩罚,来自适应调节预估代价 H 的值,使得预估代价约等于真实代价,提高算法的效率。
传统的A*算法中,算法本身是未考虑环境的复杂度。经过研究证实,路径规 划算法计算的复杂性和环境搜索空间的规模成正比,例如: A* 算法的复杂性为 o(n²)(n 为节点数),降低搜索空间即可减少遍历的节点数。为此,本文提出了根据局部区域复杂度,来自适应调节节点的搜索空间,以减少算法的时间复杂度。

(a)局部区域示意图 (b)不同方位局部区域
图5-11 局部区域复杂度定义示意图
如上图5-11(a)所示,若此时当前节点为节点1,它的父节点为父节点1,则可 计算得到当前的方向为3,参考图5-11(b)可获得该方位上的局部区域,观察图5- 11(a)局部区域,明显此区域存在障碍物、威胁物和草地等,在此区域内,希望算法 能够扩大搜索范围,寻找更优路径在避免接触障碍物和威胁物。相反如果该区域不存在障碍物和威胁物体,则希望算法能够缩小搜索范围,提高效率。因此,本文量化了局部区域的信息,设计了威胁率Q。和通过率Q, 具体为:

![]()
式中:L。为局部区域,R(i,j)越野环境栅格地图值,δ,为环境敏感度,考虑到越 野智能车辆,对于草地土路能够轻松驶过,所以本文设置为0.5,可根据车辆类型 工作任务灵活选取。n₂,n, 为越野栅格地图中一行和一列均小于δ,的条数, L 和 D 为局部区域的行和列。Q,描述了环境中威胁程度的多少, Q,越大表明环境存在 越多不可通过的物体。Q,描述了环境中威胁物、障碍物等位置的混乱程度, Q,越 大表明混乱度越小。
#初始化A-start
def __init__(self, map2d, startPoint, endPoint, passTag=1.0):#map2d地图信息,startPoint起点, endPoint终点, passTag=1.0为不可行驶区域
# 开启表
self.openList = []
# 关闭表
self.closeList = []
# 寻路地图
self.map2d = map2d
# 起点终点
if isinstance(startPoint, Point) and isinstance(endPoint, Point):
self.startPoint = startPoint
self.endPoint = endPoint
else:
self.startPoint = Point(*startPoint)
self.endPoint = Point(*endPoint)
# 不可行走标记
self.passTag = passTag
def getMinNode(self):
"""
获得openlist中F值最小的节点
:return: Node
"""局部区域惩罚规则为:
Stepl: 计算当前节点与该其父节点的方向 Direction。
Step2: 根据方向 Direction, 参考图5-11(b)选择区域范围。
Step3: 计算威胁率Q。和通过率Q,。
Step4: 计算节点的预估代价函数值。
值得注意的是,值得注意的是,图5-11(b)中局部区域范围a 的取值,本文采 用正方形区域提高为了编程效率。a 的取值也影响着算法的效率,如图5-12所示,

(a)时间图
(a)Time to figure

(b)节点数
(b)Number of nodes in figure
取四个大小分别为30×30,40×40,50×50,60×60具有相同环境分布的栅格地 图,观察到:在不同规模的地图上,随着a 值的增加,算法遍历的节点数都有减少 的趋势,但是当a 值过大时,超过6时,算法的运算时长却有所增加,这是因为随 着 a 变大局部区域变大,则计算公式(5.15)和公式(5.16)需要更多时间,因此a 值应 该处于3≤a≤6, 本文选择a 为5。
#判断节点是否在关闭表中
def pointInCloseList(self, point):
for node in self.closeList:
if node.point == point:
return True
return False
#判断节点是否在开启表中,是返回该节点
def pointInOpenList(self, point):
for node in self.openList:
if node.point == point:
return node
return None
#判断开启表中是否有终点
def endPointInCloseList(self):
for node in self.openList:
if node.point == self.endPoint:
return node
return None(3)自适应评估函数
在获得方向变化惩罚 D_P、 局部区域的威胁率Q。和通过率Q, 在越野环境R下,改进的评估函数可以表示为:
f(n)=R(g(nz)+n*Step)+R,(h(n))
![]()

式中:g(ng)为节点n父节点的真实代价值, D_P为方向变化惩罚, Step为移动代 价,R(i,j)为在节点坐标(i,j)越野栅格地图值,h(n)为节点n 的预估代价,ε为环 境威胁敏感度, d 为节点到目标点的距离, d₂ 起始点到目标点的距离。值得注意 的是,为了加快计算机处理速度将移动成本增加了10倍,因为在计算预估代价时 也需增加10倍。
因此,综合考虑了真实越野地图的复杂性、方向变化、局部区域复杂度的影响。 方向变化惩罚确保了规划的路线尽可能笔直,并存在较少的拐点;越野栅格地图模 拟了实际的越野情景,让规划的路线更符合实际需要;局部区域复杂度惩罚则提高 了算法的高效性,当环境危险度较低时,则使启发函数权重增加,进而减小搜寻空 间,从而提升搜寻效率,相反当环境危险度高时,则使启发函数权重降低,从而扩大搜寻空间,提升搜寻精度,当环境通过率较低时,表明环境的混乱程度较大,则使真实代价函数权重提高,拓展了搜寻空间,反之降低权权重。将越野环境信息与 智能汽车的位置信息相结合,并针对不同场景,通过权重函数实现自适应调节,从 而自主调整算法的有效搜索空间,不但能够提高计算的高效性与灵敏度,还保证了路径的全局最优。
5.3.4双向Floyd 算法优化路径
Floyd 算法是一种利用动态规划思想寻找多源点之间最短路径的算法之一。根 据之前小节规划出的路径可能存在多余拐点、路径并非最优的情况,因此针对此问 题,本节提出了改进的 Floyd 算法,设计了双向优化处理来实现双向平滑优化;设计了安全距离,来保证优化了路径避免与障碍物威胁物等发生碰撞。
首先增添防碰撞安全距离预警,首先设置的安全距离 D, 接着计算威胁物点到 连线的垂直距离L, 判断安全距离与垂直距离的关系,从而判断优化的路径是否安 全。如图5-13 所示,设点a坐标为(x,ya), 点S 坐标为(xs,ys), 点n₃的坐标为 (xa,Ya), 则可以计算得到点a 距离直线 S-n₃的距离 L。安全距离的设置还与地图 位置有关,由于智能越野车辆能够较为轻松驶过道路通行系数小于0.8的道路,因此安全距离具体为:

式中: cell₄ 为单元栅格的长度。因此,优化的路径要保证距离威胁物的距离要满足
L≥D。
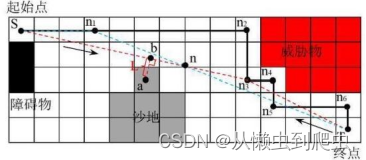
图5-13 双向 Floyd 算法示意图
双向 Floyd 算法优化路径具体步骤为:
Stepl: 从起始点 S 开始,设置 S 为开始点,按步长 k 取下一路径点1,计算 距离 L 与安全距离D 并判断小大,若满足L≥D 则取下一路径点2,直至存在不满 足L≥D 的路径点n, 则重新设置点n-1 为开始点,继续取点循环以上步骤直至遇到终点T 循环结束。
#障碍物分布
def obstacle_dis(self,minF):
if minF.father==None:
return 1
angle=self.Angle(minF.father.point,minF.point)#主方向
#print(angle)
if angle==1:
x_left=minF.point.x-2
x_right=minF.point.x+2
y_up=minF.point.y-5
Step2: 反向 Floyd 算法,将终点T 设置为开始点,按 Stepl 反向遍历路径点 直至遇见起始点 S 循环结束。
Step3: 若正向 Floyd算法优化路径与反向 Floyd 算法优化路径存在交点,则取 两者交集;若不存在交点,则于拐点数与路径长度和小的路径。
QQ767172261