题目

Description

给出一棵有N个结点的树，给出Q个询问，求结点xj过结点K到节点yj的最短距离

Format

Input

第一行一个数n

接下来共有n-1行，三个数u,v,len表示u和v之间存在一条边长为len

再给你Q，K。代表有Q个询问，K就是那个必经过

接下来Q行，每行两个数字xj,yj

N,Q<=1e6

len<=1e9

Output

如题

Samples

输入数据 1

5
1 2 1
1 3 1
2 4 1
3 5 1
3 1
2 4
2 3
4 5

Copy

输出数据 1

3
2
4

注:样例模拟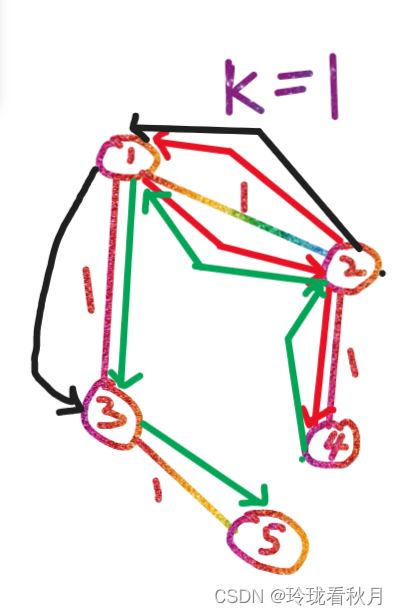 

---

 思路:

这个题是唬人的，既然是一棵树则两点之间的距离是唯一的。只是他还要求经过点k,那么为了方便,我们以k为树根，计算出每个点到k的距离，计为dis[x],则x到y的距离就是 dis[x] + dis[y]。

那么问题来了:我们怎么计算dis呢?一开始我是想用迪杰斯特拉的,但是后来才发现不需要，因为树上两点的距离是固定的,用迪杰斯特拉会有松弛操作,可这里2点之间的距离不会被更新的。所以只要用个dfs从k开始遍历整棵树,并用s记录遍历到目前节点的边的权重之和，每往下遍历一个子节点就把dfs参数中的s加上该边边权即可。

---

代码:

#include <bits/stdc++.h>
using namespace std;
#define int long long
/*
pre[i]:对于第i条边来说，它的上一条边是哪一条边
now[x]:对于点x来说，最后一条描述它充当父结点的边是哪一条边
son[i]:在第i条边中，充当子结点的点是哪一个
bq[i]:在第i条边中，边权是多少
*/
int eg,pre[1000001],now[1000001],son[1000001],bq[1000001],n,dis[1000001],q,k;
void dfs(int beg,int fa,int s)//beg:从哪个点开始dfs   fa:beg父节点的编号   s:此时从根遍历到beg的权重总和
{
  dis[beg] = s;
  for(int i = now[beg]; i; i = pre[i])//遍历beg的子节点
    if(son[i] != fa)
      dfs(son[i],beg,s + bq[i]);
}
void adeg(int u,int v,int w)
{
  pre[++eg] = now[u];
  bq[eg] = w;
  now[u] = eg;
  son[eg] = v;
}
signed main()
{
  cin>>n;
  for(int i = 1; i < n; i++)
  {
    int u,v,w;
    cin>>u>>v>>w;
    adeg(u,v,w);
    adeg(v,u,w);
  }
  cin>>q>>k;
  dfs(k,0,0);
  while(q--)
  {
    int a,b;
    cin>>a>>b;
    cout<<dis[a] + dis[b]<<endl;
  }
  return 0;
}