目录
一.引言
二.奇异值分解理论
1.行矩阵 RowMatrix
2.奇异值分解算法
三.奇异值分解实战
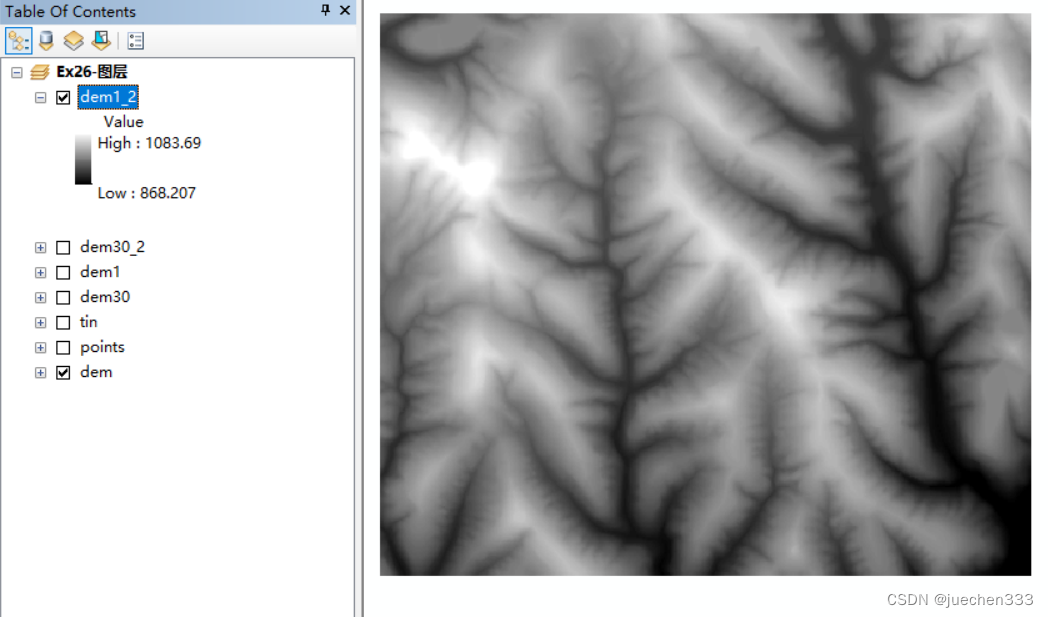
1.构建 RowMatrix
2.奇异值分解 SVD
四.总结
一.引言
奇异值分解是矩阵分解计算的一种常用方法,矩阵分解主要用于数据降维,通过将高维的数据映射到低维,实现特征的降维与特征重要性筛选。
二.奇异值分解理论
1.行矩阵 RowMatrix
介绍奇异值分解与矩阵分解前,首先熟悉下 Spark 的 RowMatrix 行矩阵,我们可以将行矩阵看作是包含若干个行向量 vector 的特征矩阵集合,每一行就是一个具有相同格式的向量集合。
new RowMatrix(rows: RDD[Vector])
new RowMatrix(rows: RDD[Vector], nRows: Long, nCols: Int)rows 代表数据列表、nRows 代表行数、nCols 代表列数。我们可以通过混合的方式,同时构造 SparseVector 与 DenseVertor:
// 加载向量
val data = Array(
Vectors.sparse(5, Seq((1, 1.0), (3, 7.0))),
Vectors.dense(2.0, 0.0, 3.0, 4.0, 5.0),
Vectors.dense(4.0, 0.0, 0.0, 6.0, 7.0)
)
//转换成RowMatrix的输入格式
val data1 = spark.sparkContext.parallelize(data)当然这里 SparseVector 也不一定要与 DenseVector 维度保持一致,SparseTensor 可以比 Dense 长但不能比 DenseVector 短。
2.奇异值分解算法
奇异值分解 (SVD) 是线性代数中重要的矩阵分解方法,一般来说一个矩阵可以使用其特征向量来表示,即矩阵 A 可以表示为:
这里 V 成为特征向量 λ 对应的特征值,首先需要注意的是,任意一个矩阵与一个向量相乘后,相当于进行了一次线性转换,例如:
可以认为一个矩阵在计算过程中是一个将其在一个方向拉伸的过程,需要关心的是拉伸的方向与幅度。一般情况下,拉伸幅度在线性变换中是可以忽略或近似计算的常量,我们仅仅需要关心的就剩其拉伸的方向了。当矩阵维数确认时,可以将其分解为若干个带有方向特征的向量,获取其不同的变换方向从而确定出矩阵。
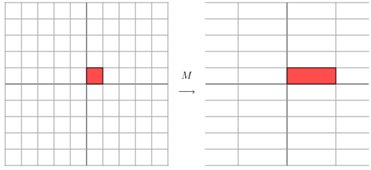
基于上述解释,可以简单的把奇异值分解 SVD 理解为 - 将一个矩阵分解为带有方向向量的矩阵相乘:
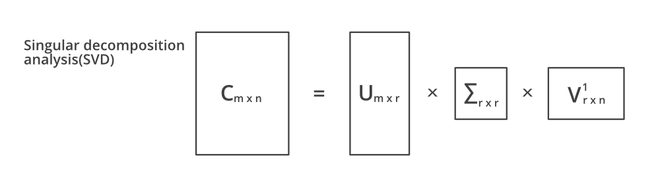
其中 U 是一个 mxr 的矩阵,∑ 是一个 rxr 的方阵,而 V 是一个 nxr 的矩阵,这三个方阵相乘得到一个 C 的近似。这样做的好处是可以极大的减少矩阵的存储空间,很多数字矩阵经过 SVD 处理后,可以获得10倍的空间缩减,从而大大提高效率。
三.奇异值分解实战
1.构建 RowMatrix
val spark = SparkSession
.builder //创建spark会话
.master("local") //设置本地模式
.appName("SVD") //设置名称
.getOrCreate() //创建会话变量
// 加载向量
val data = Array(
Vectors.sparse(5, Seq((1, 1.0), (3, 7.0))),
Vectors.dense(2.0, 0.0, 3.0, 4.0, 5.0),
Vectors.dense(4.0, 0.0, 0.0, 6.0, 7.0)
)
data.foreach(v => {
println(v)
})
//转换成RowMatrix的输入格式
val data1 = spark.sparkContext.parallelize(data)构建一个 SparseVector 两个 DenseVector 组成的矩阵,矩阵维度为 3x5。
2.奇异值分解 SVD
// 建立模型
val rm = new RowMatrix(data1) //读入行矩阵
val SVD = rm.computeSVD(2, computeU = true) //进行SVD计算
println(SVD) //打印SVD结果矩阵
val U = SVD.U
val s = SVD.s
val V = SVD.V
println(U.numRows(), U.numCols())
println(s)
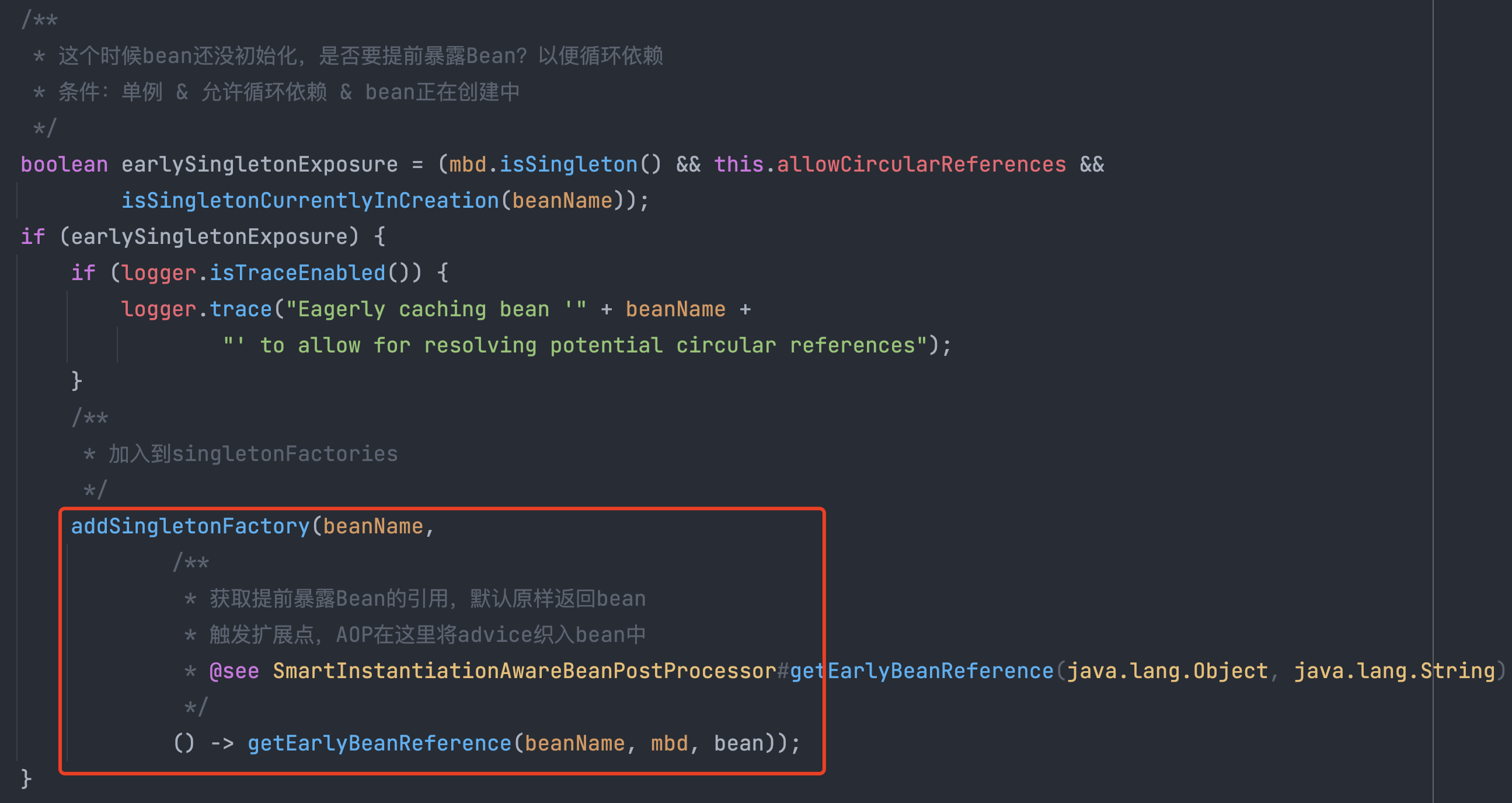
println(V.numRows, V.numCols)通过 SVD.U、SVD.s、SVD.V 可以分别获得 U、∑、V 矩阵,这样我们无需保存完整的大矩阵,只需保存三个相对较小的矩阵即可对原始矩阵的向量进行复原,这在一定程度上和 DNN 感知机比较像。
(3,2)
[13.029275535600473,5.368578733451684]
(5,2)四.总结
上面的示例中展示了低维情况下的数据变换,如果矩阵在高维状态下,通过与 vector 相乘达到线性变换的场景我们可能无法用图像表示。但是变换同样是多个方向的,我们通过特征值分解可以得到前 N 个特征向量从而提取前 N 个特征的方向,通过 N 个方向的变换近似矩阵整体的方向变换,达到降维的需求。完整的推理过程打击可以参考:Singular Value Decomposition (SVD) tutorial。