1 回溯算法
回溯算法具有通用性,但是算法的效率不高,通常可以通过剪枝等操作提高算法的效率。
算法思想:
在包含问题的所有解空间树中,按照深度优先搜索的策略,从根节点出发,深度搜索解空间树。当搜索到某一个节点时候,先判断该节点是否包含问题的解,如果包含就从该节点触发继续深度搜索下去,否则回溯;
解空间:
解空间就是所有解的可能取值构成的空间,一个解往往包含了得到这个解的每一步,往往就是对应解空间树中一条从根节点到叶子节点的路径。子集树和排列树都是一种解空间,它们不是真实存在的数据结构,也就是说并不是真的有这样一颗树,只是抽象出的解空间树。
1.1 解空间—子集树
子集树通常用于求某个问题的子集,涉及到子集的问题,看是否可以用子集树方式。
void func(int arr[], int i, int length,int x[])
{
if (i == length)
{
for (int j = 0; j < length; j++)
{
if (x[j] == 1)
{
cout << arr[j] << " ";
}
}
cout << endl;
}
else
{
x[i] = 1; // 选择i节点
func(arr, i + 1, length,x); // 遍历 i 的左孩子
x[i] = 0; // 不选择i节点
func(arr, i + 1, length,x); // 遍历i的右孩子
//func(arr, i + 1, length); // 三叉树
}
}
int main()
{
int arr[] = { 1, 2, 3 };
int length = sizeof(arr) / sizeof(arr[0]);
int x[3] = { 0 };
func(arr, 0, length,x);
system("pause");
return 0;
}
对代码的理解:
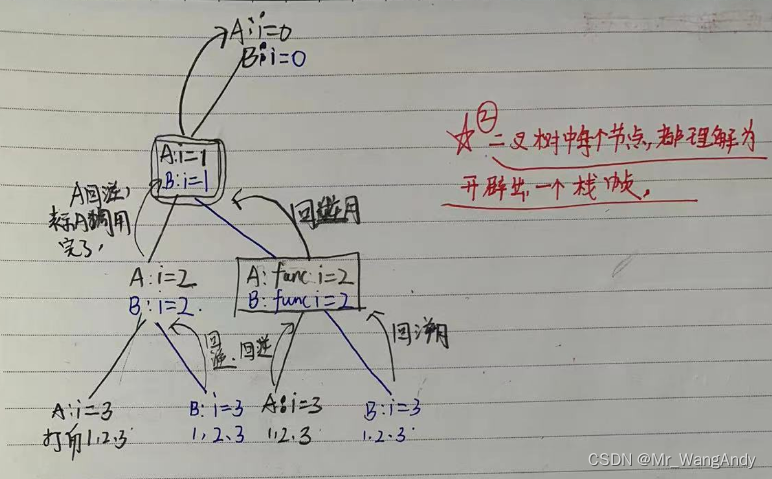
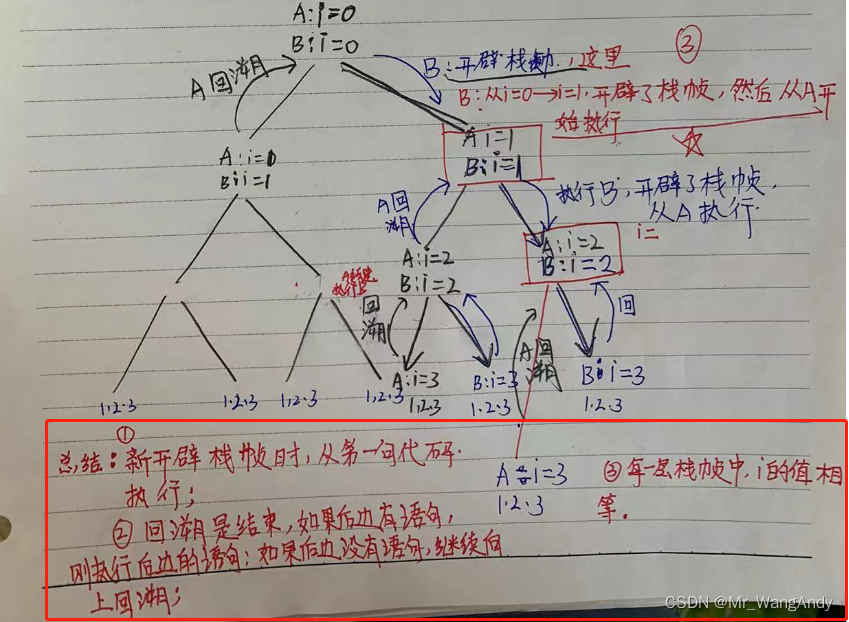
子集树中的两个循环,在逻辑上生成二叉树。
上面在递归过程中,一个节点(栈帧),向左递归标记为1,向右标记为0,打印时候,按照条件打印。
上边对递归左右走做一个标记,出来的就是子集树。算法时间复杂度,O(2^n)。
子集树总结
1 , 新开辟的栈帧中,从第一句代码开始执行;即使,第二句代码开辟的栈帧,仍然从新开辟的栈帧的第一句开始执行;
2 , 回溯就是结束,回溯到上一个节点后,如果后边有语句,继续执行后边的语句;
3 , 每一层栈帧中i节点相同,也就是层数相同。


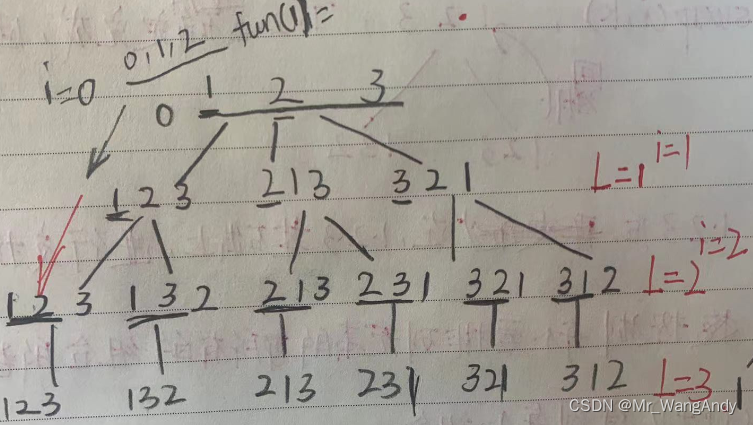
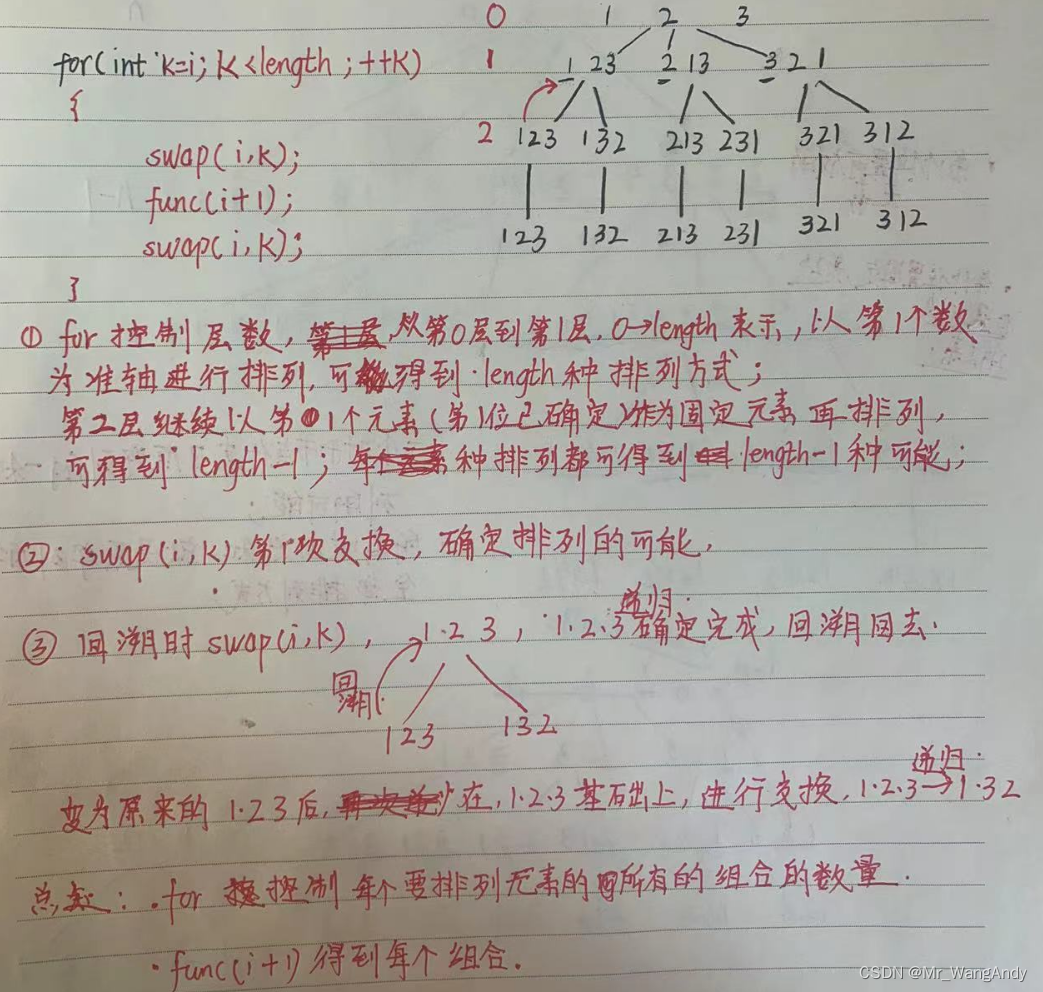
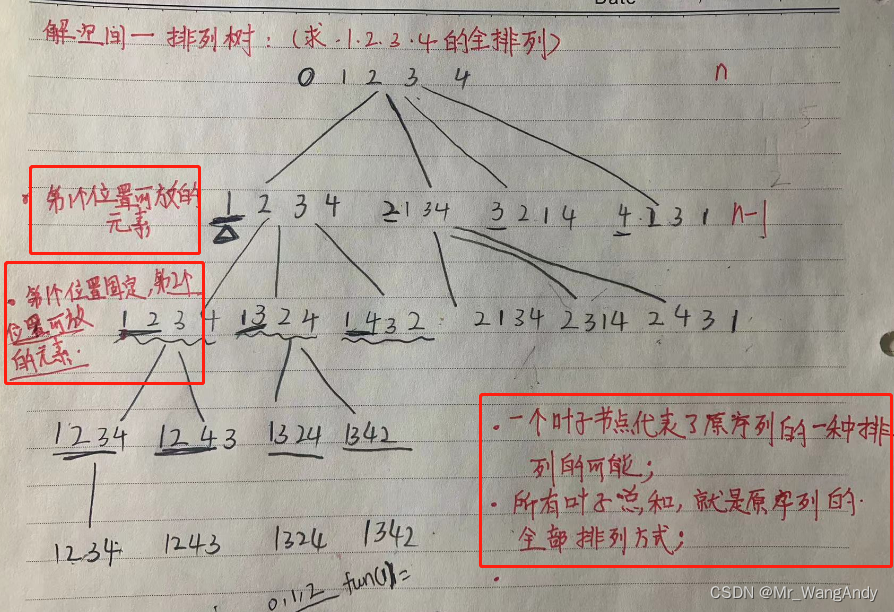
1.2 解空间— 排列树
排列树就是获取某个集合的全排列,比如求1 2 3这组数的全排列;
假如求1 2 3 全排列
void swap(int arr[], int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void func(int arr[], int i, int length)
{
if (i == length)
{
for (int j = 0; j < length; j++)
{
cout << arr[j] << " ";
}
cout << endl;
}
else
{
for (int k = i; k < length; k++)
{
swap(arr, i, k);
func(arr, i + 1, length);
swap(arr, i, k);
}
}
}
int main()
{
int arr[] = { 1,2,3 };
int length = sizeof(arr) / sizeof(arr[0]);
func(arr, 0, length);
system("pause");
return -1;
}


1.3 整数选择问题
整数选择:给定一组整数,从里面挑选出一组整数,让选择的整数的和 与 剩下的整数的和的差最小;
int min = 10000;
int result = 0;
int Xsum = 0; // 记录选择的元素之和
int Ysum = 0; // 记录没有选择的元素之和
void func(int arr[],int i,int length,int x[])
{
if (i == length)
{
for (int j = 0; j < length; j++)
{
if (x[j] == 1)
{
}
else
{
Ysum += arr[j]; // 记录未选择的元素之和
}
}
result = abs(Xsum - Ysum);
Xsum = 0;
Ysum = 0;
if (result <= min)
{
min = result;
}
cout << endl;
}
else
{
x[i] = 1;// 1 从当前节点向左走
Xsum += arr[i];
func(arr, i + 1, length,x);
Ysum += arr[i];
x[i] = 0; // 2 回溯到父节点,然后从父节点向右走
func(arr, i + 1, length,x);
}
}
int main()
{
int arr[] = { 12,6,7,11,16,3,8 };
int length = sizeof(arr) / sizeof(arr[0]);
int x[7] = { 0 };
func(arr, 0, length,x);
cout << "选择和剩下的整数之和为:" << min << endl;
system("pause");
return 0;
}
1.4 2N整数选择问题-加入剪枝操作
给2n个整数,从里面挑选出n个整数,让选择的整数的和 与 剩下的整数的和的差值最小;
int arr[] = { 12,6,7,11,16,3,5,23};
int length = sizeof(arr) / sizeof(arr[0]);
vector<int> bestM; // 记录选择的最小值
vector<int> M; // 记录子集中选择的元素
unsigned int minval = 0xffffffff;
int sumR = 0; // 记录数组中未被选择的元素之和
int sumS = 0; // 记录选中的数组元素总和
int cnt = 0; // 记录遍历的子集的个数
int left1 = length;
// 未加入剪枝操作
void func1(int i)
{
if (i == length)
{
cnt++;
if (M.size() != length / 2)
{
return;
}
int result = abs(sumS - sumR);
if (result < minval)
{
minval = result;
bestM = M;
}
}
else
{
M.push_back(arr[i]); // 记录选择的元素
sumR -= arr[i];
sumS += arr[i];
func1(i + 1);
// a
cout << endl;
sumS -= arr[i];
sumR += arr[i];
M.pop_back();
func1(i + 1);
}
}
// 加入剪枝操作
void func(int i)
{
if (i == length)
{
cnt++;
if (M.size() != length / 2)
{
return;
}
int result = abs(sumS - sumR);
if (result < minval)
{
minval = result;
bestM = M;
}
}
else
{
left1--;
if (M.size() < length / 2) // 减左树枝,还未选择够n个整数
{
// 下面三行,递归做的事情
M.push_back(arr[i]); // 记录选择的元素
sumR -= arr[i];
sumS += arr[i];
func(i + 1);
// 回溯
sumS -= arr[i];
sumR += arr[i];
M.pop_back();
}
// 右树枝可以选吗?已选择的数字的个数 + 未来能选择的所有数组个数(i+1,i+2,...i+n) >= n个元素
// 已选择的数字的个数 + 未来能选择的所有数组个数(i+1,i+2,...i+n) <= n个元素 则不执行
if (M.size() + left1 >= length / 2)
{
func(i + 1);
}
left1++;
}
}
int main()
{
// 计算出数组总和
for (int v : arr)
{
sumR += v;
}
func(0);
cout << "最小值" << minval << endl;
for (int v : bestM)
{
cout << v << " ";
}
cout << endl;
cout << "cnt: " << cnt << endl;
system("pause");
return 0;
}
1.5 挑选一组数字,让他们的和等于指定的值
挑选数字:有一组整数,请挑选出一组数字,让他们的和等于指定的值,存在解打印,不存在打印
int arr[] = { 12,6,7,11,16,3,5,23 };
const int number = 34;
int length = sizeof(arr) / sizeof(arr[0]);
vector<int> x; // 记录选择的数字
int sum = 0; // 记录选择的数字之和
int r = 0; // 记录未处理的数字的和
void func(int i)
{
if (i == length)
{
if (sum != number)
{
return;
}
for (int v : x)
{
cout << v << " ";
}
cout << endl;
}
else
{
r -= arr[i];
// 加入剪枝操作,减左枝: 如果已选择的数字的和 + 加上即将选择的的数字的和 < number
if (sum + arr[i] <= number)
{
sum += arr[i]; // 记录所选数字之和
x.push_back(arr[i]);
func(i + 1);
sum -= arr[i]; // 减去右子树中的元素
x.pop_back();
}
if (sum + r >= number)
{
func(i + 1);
}
r += arr[i];
}
}
int main()
{
for (int v : arr)
{
r += v;
}
func(0);
// 计算出数组总和
system("pause");
return 0;
}

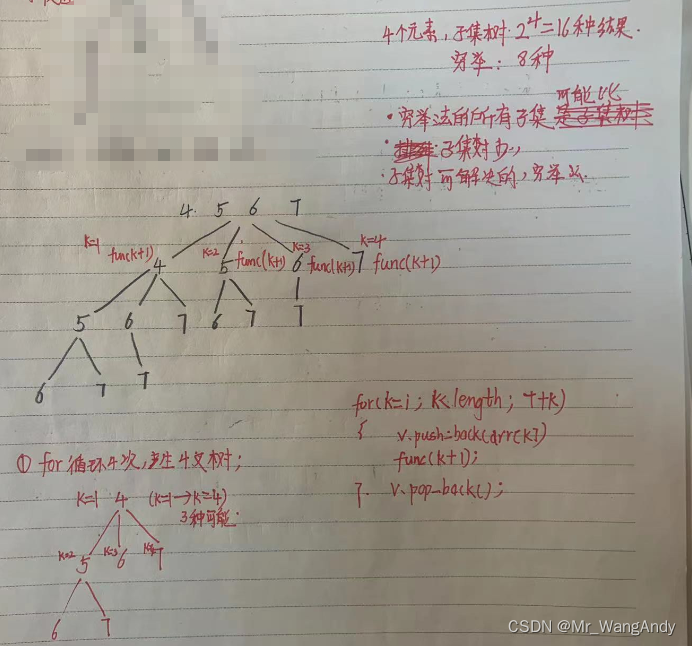
1.6 穷举法 (挑选数字)
穷举法和子集树的关系:穷举法所有的可能是子集树的子集;子集树能解决的问题,穷举法可能解决不了;
对代码的理解:
for的第一层 1 2 3 4 ;以1为确定的值第二层 2 3 4 ,以2为可能值的第2层,3,4;等等。
int arr[] = { 12,6,7,11,16,5,5,23 };
int number = 34;
int length = sizeof(arr) / sizeof(arr[0]);
vector<int> vec; // 存放选择的数字
void func(int i, int number)
{
if (number == 0)
{
for (int v : vec)
{
cout << v << " ";
}
cout << endl;
}
else
{
for (int k = i; k < length; k++)
{
if (number >= arr[k])// number大于下一个元素,比如number=8,下一个元素为13,不满足;如果下一个元素为3,number>=3,满足
{
vec.push_back(arr[k]);
func(k + 1, number - arr[k]); // Andy: k+1这种方式表示不允许重复选择元素,只能遍历当前元素的孩子节点
//func(k, number - arr[k]);// Andy: k这种方式表示允许重复选择元素,只能遍历当前元素的孩子节点
vec.pop_back();
}
}
}
}
int main()
{
func(0,number);
// 计算出数组总和
system("pause");
return 0;
}
1.7 0-1背包
有一组物理,其重量分别是w1 w2 w3,,其价值分别是v1 v2 ,vn,现在有一个背包,其容量是C,问怎么把物品装入背包,能够使背包的价值最大化。
解法:用子集树求解
int w[] = { 12,5,8,9,6 }; // 物品的重量
int v[] = { 9,2,4,7,8 }; // 物品的价值,物品和价值是一对一关系
int C = 25;
const int length = sizeof(w) / sizeof(w[0]);
int cw = 0; // 已经选择的物品的重量;
int cv = 0; // 已经选择的物品的价值
vector<int> x; // 记录已经选择的物品
vector<int> bestx; // 记录最优解
int bestv = 0;
int r = 0; // 记录剩余元素的总价值
int cnt = 0;
void func(int i)
{
if (i == length)
{
cnt++;
if (C == cw)
{
if (bestv < cv)
{
bestv = cv;
bestx = x;
}
}
}
else
{
r -= v[i];
// 开始加入剪枝操作,减左枝
if (cw + w[i] <= C) // 已选择物品重量 + 即将选择的物品重量,小于总容量再操作
{
x.push_back(w[i]);
cw += w[i];
cv += v[i];
func(i + 1);
x.pop_back();
cw -= w[i];
cv -= v[i];
}
// 加入减右枝操作
if (cv + r > bestv)
{
func(i + 1);
}
r += v[i];
}
}
int main()
{
for (int v : v)
{
r += v;
}
func(0);
cout << "cnt" << cnt << endl;
cout << "选择的物品重量为:";
for (int w : bestx)
{
cout << w << " ";
}
cout << endl;
cout << "最优值为:" << bestv << endl;
system("pause");
return 0;
}
1.8 排列树解决N-皇后问题
8*8的格子中,任意两个棋子不能出现在同一行,同一列,同一条斜线上。
int cnt = 0;
// 8皇后问题
bool judge(int arr[], int i)
{
for (int j = 0; j < i; j++)
{
if (i == j || arr[i] == arr[j] || abs(i - j) == abs(arr[i] - arr[j]))
{
return false;
}
}
return true;
}
//
void swap(int arr[], int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void func(int arr[], int i, int length)
{
if (i == length)
{
cnt++;
for (int j = 0; j < length; j++)
{
cout << arr[j] << " ";
}
cout << endl;
}
else
{
for (int k = i; k < length; ++k)
{
swap(arr, i, k);
if (judge(arr, i))
{
func(arr, i + 1, length); // 每次从上层遍历到下层的过程中,每向下一层,理解为选择每行每列的过程;
} // 遍历到第i层时候,都要判断0 -- i-1层,是否满足条件
swap(arr, i, k);
}
}
}
int main()
{
int arr[] = { 1,2,3,4 ,5,6,7,8}; // arr数组下标表示行,下标对应位置表示列;
int n = 8;
int length = sizeof(arr) / sizeof(arr[0]);
func(arr, 0, length);
cout << "cnt = " << cnt << endl;
system("pause");
return -1;
}
1.9 穷举法生成排列树
int arr[] = { 1,2,3 };
int length = sizeof(arr) / sizeof(arr[0]);
vector<int> vec;
int state[3] = { 0 }; // 1表示选择了,0表示未选择
void func(int i)
{
if (i == length)
{
for (int v : vec)
{
cout << v << " ";
}
cout << endl;
}
else
{
for (int k = 0; k < length; ++k)
{
if (state[k] == 0)
{
state[k] = 1;
vec.push_back(arr[k]);
func(i + 1);
vec.pop_back();
state[k] = 0;
}
}
}
}
int main()
{
func(0);
system("pause");
return -1;
}

1.10穷举法func(k+1) 与 排列树中的fun(i+1)中,i 和 k区别?
穷举法中的k表示可选择的元素的起始下标,并且选择的数量不同,树的深度不同。
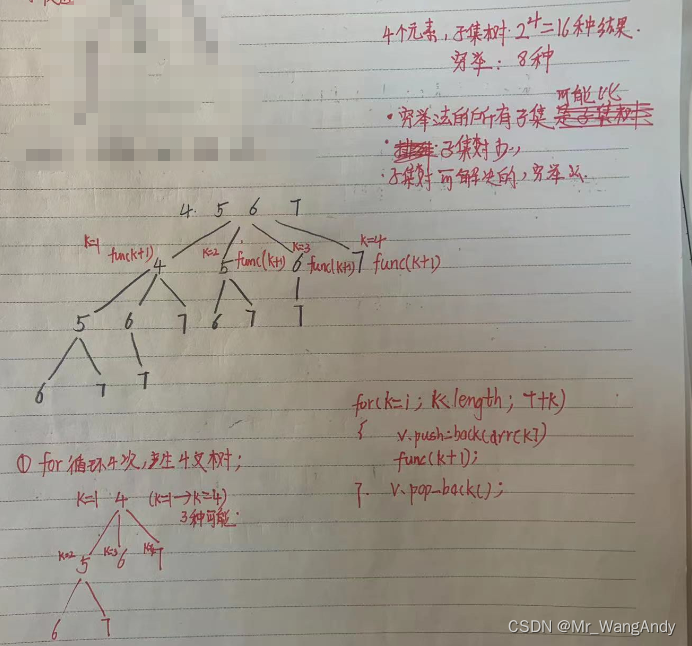
排列树中的i表示的是层数,排列树最后生成的是平衡树,树的深度相同。