系列文章目录

前言

目的：学习整数在内存的储存，什么是大小端，浮点数的储存。

1. 整数在内存中的存储

在讲解操作符的时候，我们就讲过了下⾯的内容：

整数的2进制表⽰⽅法有三种，即 原码、反码和补码。

正整数的原、反、补码都相同。

负整数的三种表⽰⽅法各不相同。

原码：直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。

反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。

补码：反码+1就得到补码，补码也可以取反+1得到源码。

三种表⽰⽅法均有符号位和数值位两部分，符号位都是⽤0表⽰“正”，⽤1表⽰“负”，⽽数值位最

⾼位的⼀位是被当做符号位，剩余的都是数值位。

数据存放内存中其实存放的是补码。 为什么呢？

在计算机系统中，数值⼀律⽤补码来表⽰和存储。

原因在于，使⽤补码，可以将符号位和数值域统⼀处理；

同时，加法和减法也可以统⼀处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是

相同的，不需要额外的硬件电路。

2. ⼤⼩端字节序和字节序判断

当我们了解了整数在内存中存储后，我们调试看⼀个细节：

 

#include <stdio.h>
int main()
{
 int a = 0x11223344;
 
 return 0;
}

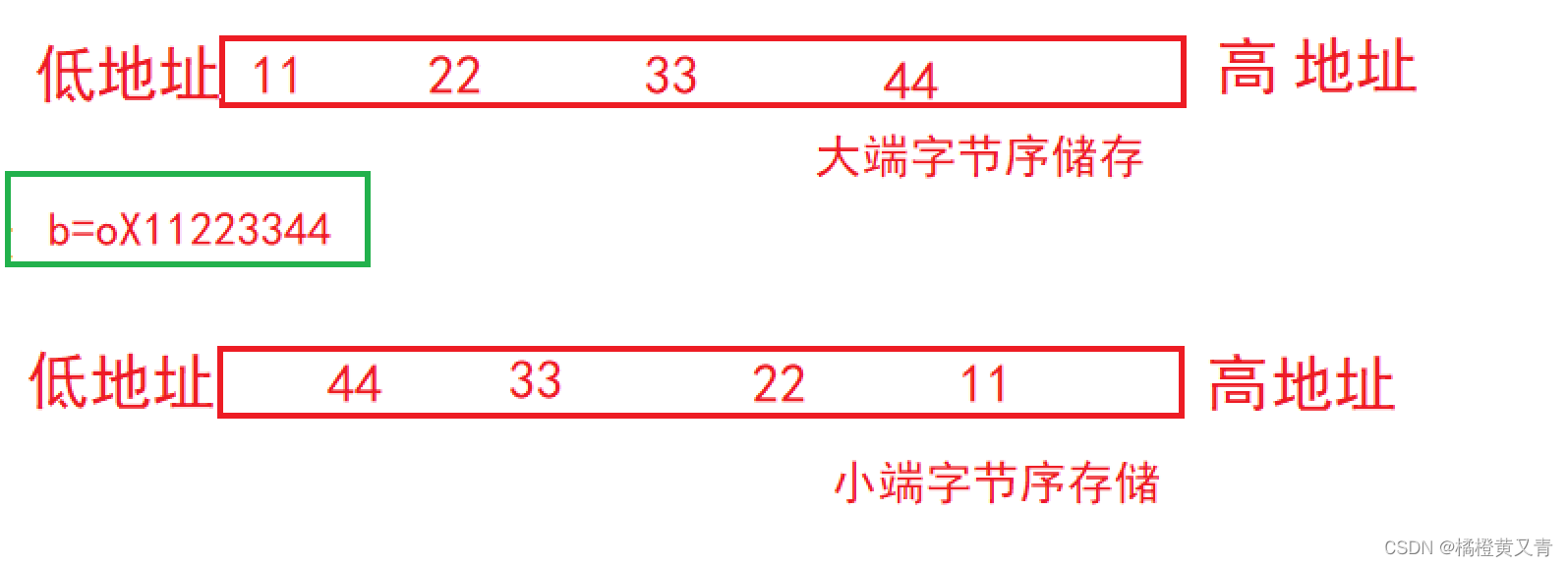
调试一下，我们可以看到在a中的 0x11223344 这个数字是按照字节为单位，倒着存储的。

2.1 什么是⼤⼩端？

其实超过⼀个字节的数据在内存中存储的时候，就有存储顺序的问题，按照不同的存储顺序，我们分 为⼤端字节序存储和⼩端字节序存储，下⾯是具体的概念：

1.⼤端（存储）模式：是指数据的低位字节内容保存在内存的⾼地址处，⽽数据的⾼位字节内容，保存 在内存的低地址处。

2.⼩端（存储）模式：是指数据的低位字节内容保存在内存的低地址处，⽽数据的⾼位字节内容，保存 在内存的⾼地址处。

上述概念需要记住，⽅便分辨⼤⼩端。

 图片展示一下：

 2.2 为什么有⼤⼩端?

//代码1
#include <stdio.h>
int check_sys()
{
     int i = 1;
     return (*(char *)&i);//下面分析：
}
int main()
{
     int ret = check_sys();
     if(ret == 1){
         printf("⼩端\n");
        }
     else{
         printf("⼤端\n");
     }
     return 0;
}

下面我们 来做一些有关数据的储存的练习：

案例1：

#include <stdio.h>
int main()
{
     char a= -1;
     signed char b=-1;
     unsigned char c=-1;
     printf("a=%d,b=%d,c=%d",a,b,c);
     return 0;
}

输出结果：

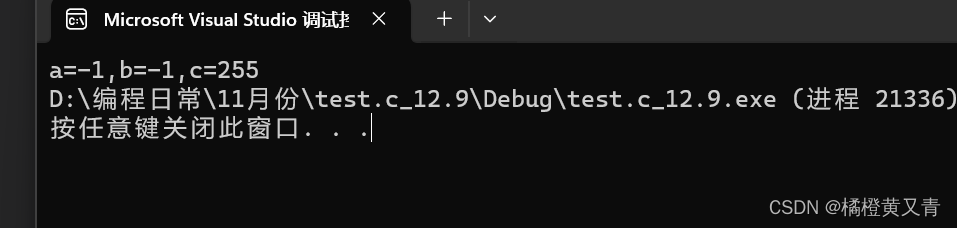
我们来一个一个分析：

 b变量也是和a是一样的

 案例2：

#include <stdio.h>
int main()
{
     char a = -128;
     printf("%u\n",a);
     return 0;
}

char的范围-128~127，那这个案例输出结果为：

这是为什么呢？

分析如图：

在这里我们记住两图，记住就行：

signed char：

 unsigned char：

案例3：

#include <stdio.h>
int main()
{
     char a[1000];
     int i;
     for(i=0; i<1000; i++){
         a[i] = -1-i;
     }
     printf("%d",strlen(a));
     return 0;
}

在这里上面那幅图就很重要了，输出结果是：

字符串长度找到\0.也就是0

循环到255时在++，变成了0，所以是255.

案例4：

#include <stdio.h>
unsigned char i = 0;
int main()
{
     for(i = 0;i<=255;i++){
         printf("hello world\n");
     }
     return 0;
}

这个一看就是死循环，unsigned char的值范围0~255，所以会一直打印hello world。

案例5：

#include <stdio.h>
int main()
{
     unsigned int i;
     for(i = 9; i >= 0; i--)
     {
         printf("%u\n",i);
     }
     return 0;
}

输出结果：

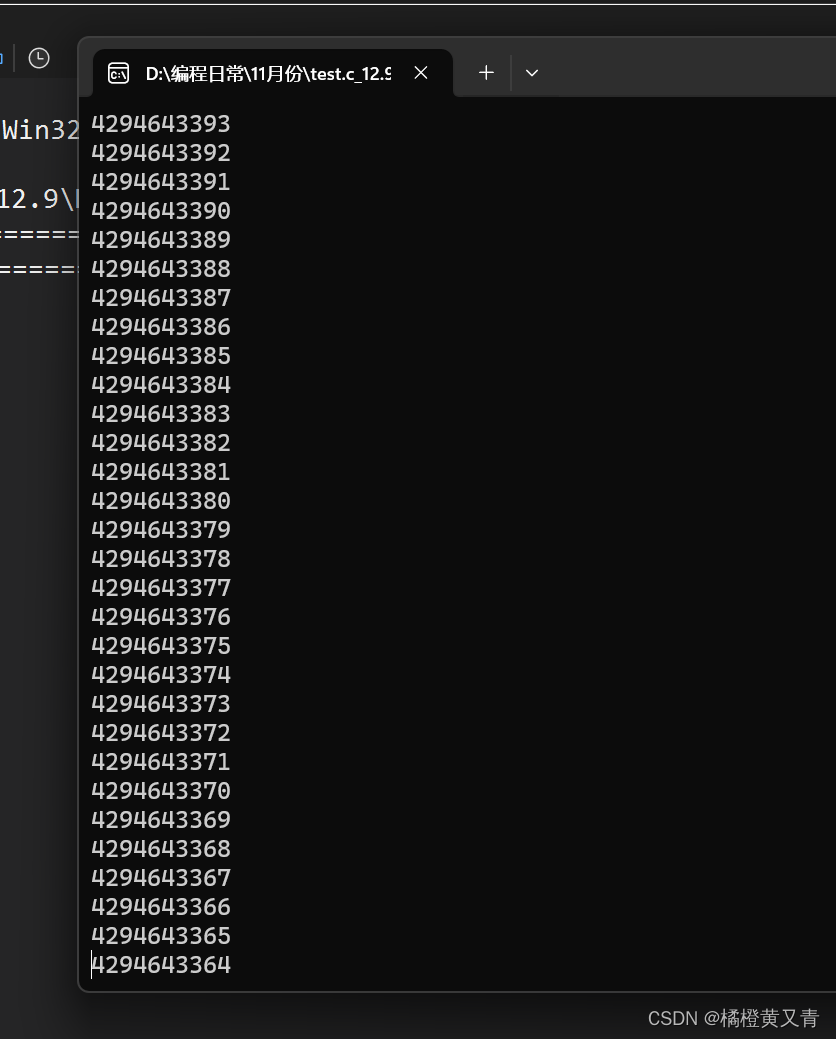
也是死循环为什么？因为i = -1时，位无符号-1的无符号是一个很大的正数，所以死循环。

3. 浮点数在内存中的存储

V   =  (−1) ^ S * M ∗ 2^E

• (−1) S 表⽰符号位，当S=0，V为正数；当S=1，V为负数

• M 表⽰有效数字，M是⼤于等于1，⼩于2的

• 2^  E 表⽰指数位

 举例来说:

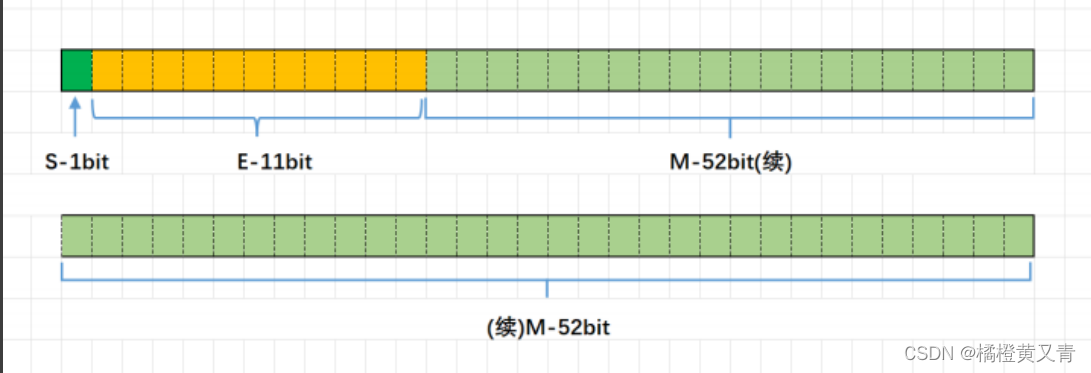
3.1浮点数存数的过程

IEEE 754 对有效数字M和指数E，还有⼀些特别规定:

#include<stdio.h>
int main()
{
    float  a = 5.5f; 
    return 0；
}

3.2浮点数取的过程 

#include <stdio.h>
int main()
{
     int n = 9;
     float *pFloat = (float *)&n;
     printf("n的值为：%d\n",n);
     printf("*pFloat的值为：%f\n",*pFloat);
     *pFloat = 9.0;
     printf("n的值为：%d\n",n);
     printf("*pFloat的值为：%f\n",*pFloat);
     return 0;
}

 所以不要把浮点数和正数打印错了。

好了，今天就到这里了，都看到这里了，点一个赞吧，谢谢观看。