目录
交换排序
冒泡排序
冒泡排序的时间复杂度
快速排序
快速排序单趟排序的时间复杂度
快速排序的时间复杂度
快速排序的优化
优化1:三数取中法
优化2:小区间优化法
交换排序
在日常生活中交换排序的使用场景是很多的,比如在学校做早操,老师通常会让学生按大小个排队,如果此时来了一个新学生,要让他进入队伍,此时就要让他先与队列的第一个学生进行比较,发生交换,最终将他排到合适的队列位置,这就是一个简单的交换排序的使用场景。在数据结构中,我们怎样实现交换排序呢?
交换排序分为冒泡排序和快速排序(重点),下来就让我们一起研究这两个排序。
冒泡排序
冒泡排序的思想:我们将冒泡排序分成了多个单趟排序,每趟排序找出最大的元素,并且将最大的元素放置于数组的末尾。
冒泡排序的单趟排序代码:
for (int i = 0; i < size -j-1; i++)
{
//比较两个元素,因为是排升序,所以如果第一个元素比第二个元素要大,就要发生交换
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
flag = 0;
}
}冒泡排序整体代码:
void BubbleSort(int* a, int size)
{
//整体的排序
for (int j = 0; j < size - 1; j++)
{
//定义一个标志变量,为循环结束的条件
int flag = 1;
//单趟排序:先让第一个元素与第二个元素进行比较大小,因为是排升序,所以如果第一个元素比第二个元素大,要发生交换,依此步骤,完成一次单趟排序
for (int i = 0; i < size -j-1; i++)
{
//比较两个元素,因为是排升序,所以如果第一个元素比第二个元素要大,就要发生交换
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
flag = 0;
}
}
//优化:如果进行了一趟排序之后,没有元素发生交换,就意味着数组已经变得有序,所以就没有必要再去进行下一趟排序了
if (flag == 1)
{
break;
}
}
}
int main()
{
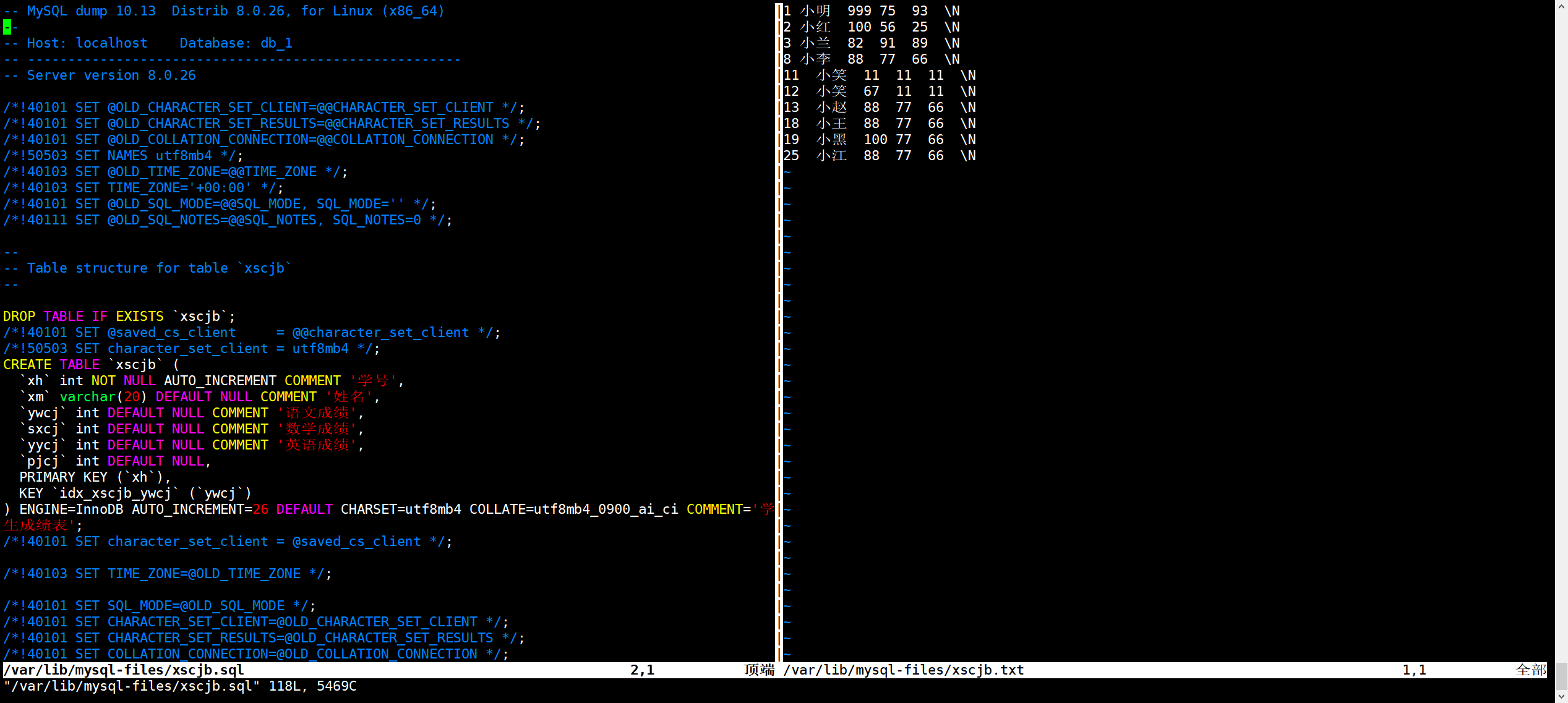
int arr[] = { 1000,999,888,777,666,555,444,333,222,111 };
BubbleSort(arr, sizeof(arr) / sizeof(int));
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{
printf("%d ", arr[i]);
}
return 0;
}运行截图如下:

注意:我们里面定义了一个flag变量为循环结束的标志,因为我们对冒泡排序做了优化,因为当一个数组已经有序时,我们人眼可以看出来,但是编译器是看不出来的,所以,我们要设置这个变量,为的就是,当我们进行了一趟排序后,如果没有发生元素的交换,证明此时数组已经变得有序了,所以就没有必要再去进行下一趟排序了,应该直接终止排序,即跳出循环。
冒泡排序的时间复杂度
时间复杂度: 最好:O(N) 最坏:O(N^2)
稳定性:稳定
快速排序
快速排序是排序中最牛也是最重要的排序。 本期我们主要讲解快速排序的递归版本。
快速排序的思想:先进行单趟排序,单趟排序找出key之后,对key左边的数组和key右边的数组依次进行快速排序,按照递归的思想最终完成排序。
单趟排序的思想:
方法一:hoare版本,这个版本是发明快排的大佬所使用的版本,有些难懂,称之为原始版本。
主要思路:1.设置两个变量left和right,分别表示数组第一个元素和最后一个元素的位置,然后规定key为left或者right的位置。
2.从left位置开始,找比key位置上的元素大的元素,从right位置开始,找比key位置上的元素小的元素,这里需要注意:如果选取left为key,应从right位置开始找,如果选取right为key,应该从left位置开始找。
3.当找到了对应的元素之后,将两个位置上的元素进行交换,分别让left++,right--然后重复上述2步骤,直到left和right处于同一位置,将此位置上的元素与key位置上的元素进行交换,然后将key挪动到此位置,一趟排序就完成了,此时key位置左边的所有位置的元素都比key位置上元素要小,key位置右边的元素都比key位置上的元素都要大,此时就证明key位置上的元素已经放到了最终的位置,排好了序。
单趟排序图示如下:
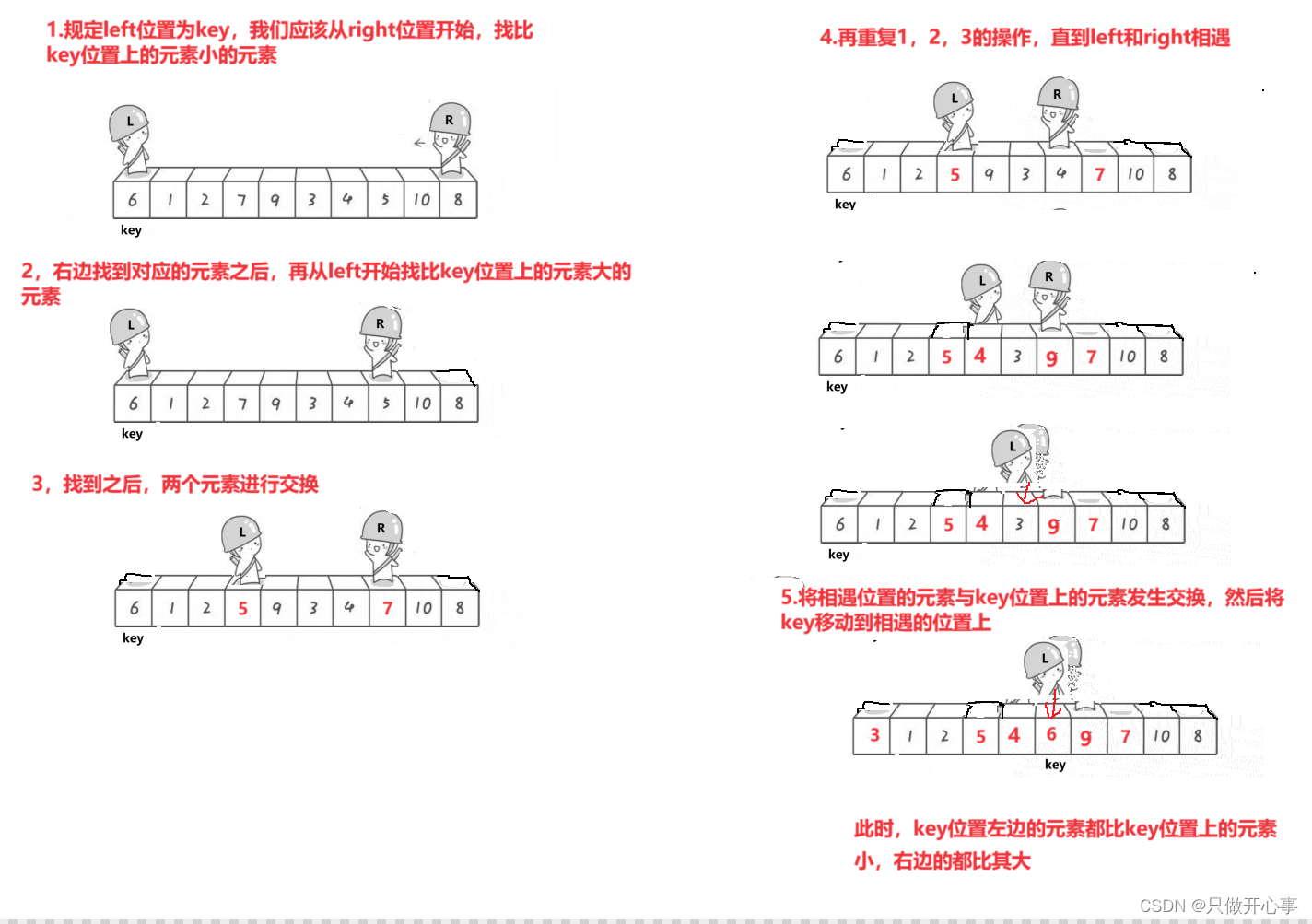
单趟排序的代码如下:
int PartSort1(int* a, int left, int right)
{
int key = left;
//进行单趟排序,找到left和right相遇的位置
while (left < right)
{
while (left<right && a[right]>=a[key])
{
right--;
}
while (left < right && a[left] <= a[key])
{
left++;
}
swap(&a[right],&a[left]);
}
swap(&a[left],&a[key]);
key = left;
}
大家注意这两行代码:
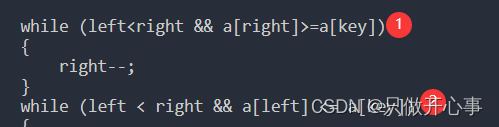
为什么限制条件必须这样写呢?因为我们要避免两种极端情景。
情景1:当数组元素相同时

![]()
当数组元素相同时,按照我们以往的算法,从right开始找比key小的,如果比key大就right--,,然后在从left开始找,找比key大的,如果比key小就left++,但是在这种情况下right不可能比key大的,所以right就不可能--,left也不可能比key值小,所以left就不可能++,里面的while循环无法正常进行,所以为了避免这样情况下我们就要,增加判断条件,即a[right]>=a[key]和a[left] <= a[key],比以往多了一个==,这样就会让left++和right--正常进行。
情景2:当数组已经是个有序数组时:
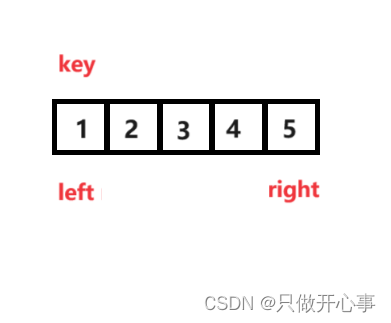
这种情景刚开始都是正常的,但是大家仔细思考下面的两行代码。
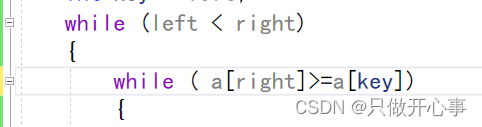
当right和left相遇之后,因为最外层的控制条件只会堆内层的循环产生一次限制影响,所以此时的right仍然会再次--,这就会导致right越界。所以我们还必须加上一个限制条件,里面的while循环也必须加上left<right的限制条件,所以改善之后的代码如下:
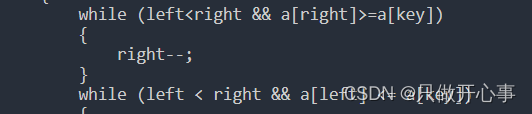
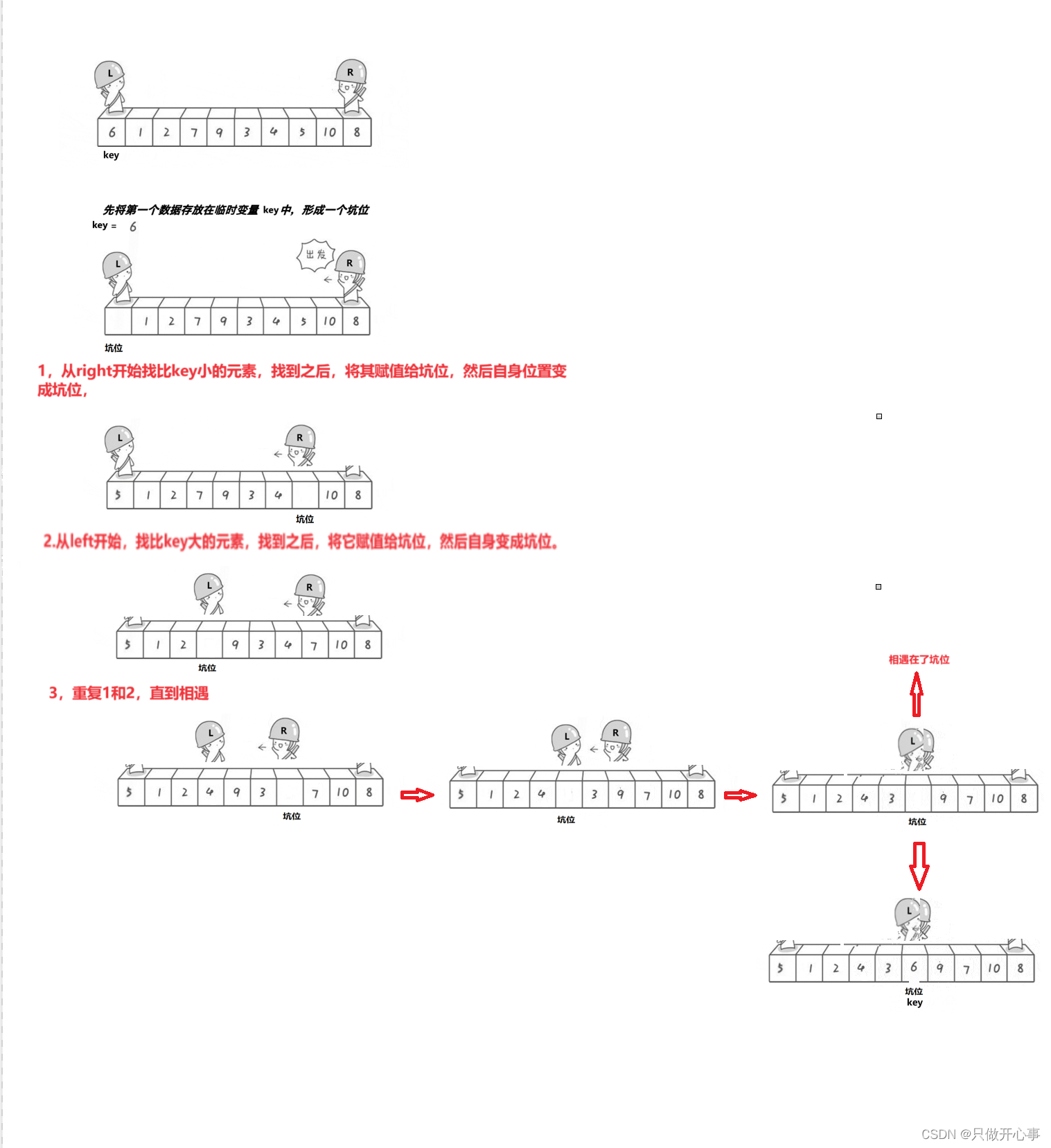
单趟排序方法二:挖坑法
主要思路:1.将第一个数据存放在临时变量key中,然后第一个位置形成一个坑位。然后从right开始找比key小的元素,找到之后与放置到坑位,然后自己成为坑位。
2.从left开始找比key大的元素,找到之后放置到坑位,然后自己形成一个坑位。
3.重复1,2,直到left和right相遇。最终将key的值放置在坑位,最红key左边的值都小于key的值,右边的值都大于key的值。
单趟排序第二种方法代码:
int PartSort2(int* a, int left,int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int key = a[left];
int pivot = left;
while (left < right)
{
while (left<right && a[right]>=key)
{
--right;
}
a[pivot] = a[right];
pivot = right;
while (left < right && a[left] <= key)
{
++left;
}
a[pivot] = a[left];
pivot = left;
}
a[left] = key;
}快速排序整体代码:
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int key= PartSort1(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
int main()
{
int arr[] = { 100,99,88,77,66,55,44,33,22,11 };
QuickSort(arr,0,sizeof(arr)/sizeof(int)-1);
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{
printf("%d ", arr[i]);
}
return 0;
}运行截图如下:

快速排序单趟排序的时间复杂度
left和right从数组两端一直到相遇,再与key交换,整个过程刚好每个元素都和key位置的元素比较了一次,所以快速排序单趟排序的时间复杂度为O(N)
快速排序的时间复杂度
最好:O(N*logN)
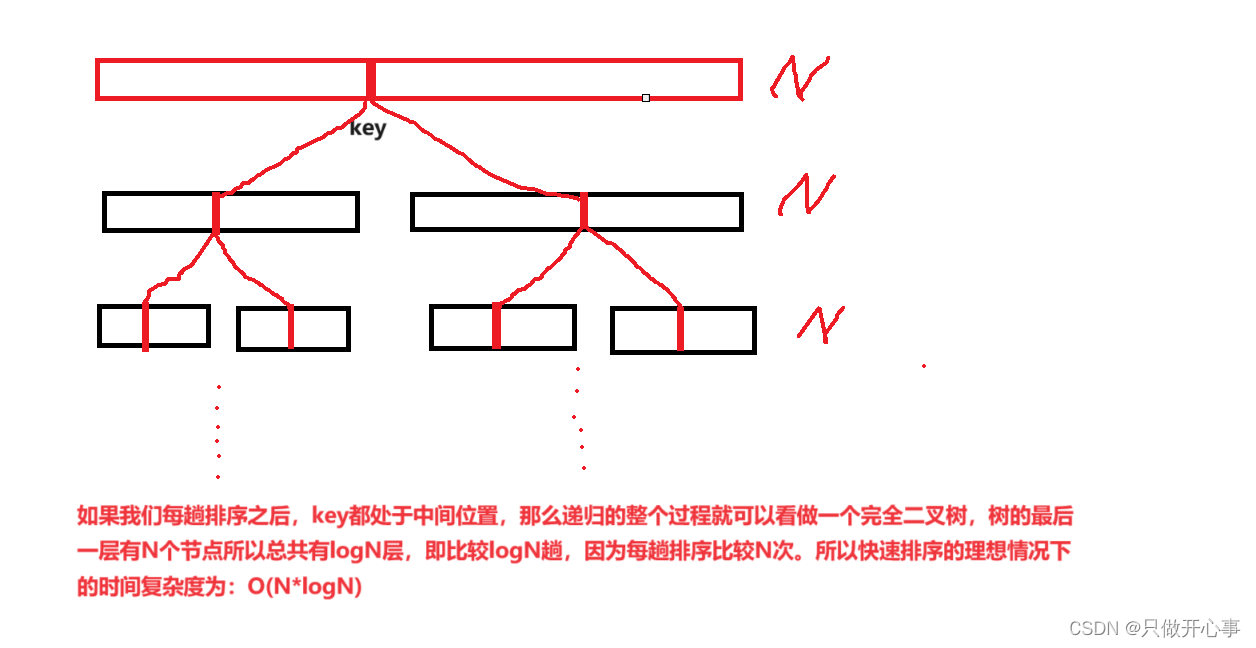
最坏:O(N^2)
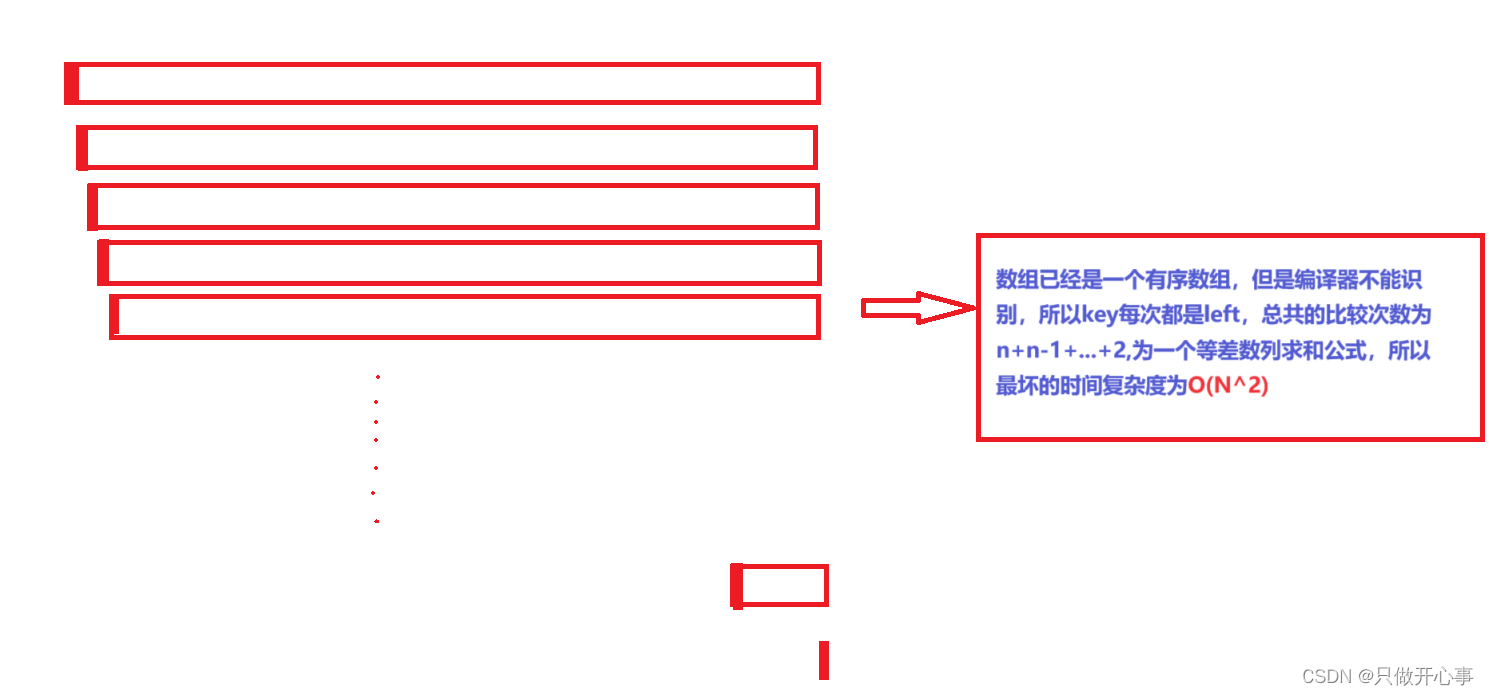
稳定性:不稳定。
综上我们知道,当数组有序时吗,快排的效率非常差劲,为了提高效率,我们发明了一种三数取中法,为一个将有序数组变称无序数组的方法,以提高效率。
快速排序的优化
优化1:三数取中法
具体思路:在进行单趟排序之前,先将left,right和(left+right)/2,位置上的元素分别进行对比,找出出刚好大小处于中间的元素,将次位置设置成mid;然后将mid位置上的元素与left位置上的元素进行交换,就导致left位置上的元素已经是数组中两个元素中间的一个元素,也就意味着进行了这样的一个调整之后,数组一定是无序的。这样就强制性的改变了快排最坏的情况,向最好的情况引导。
这就保证了,单趟排序之后,key的位置一定不是处于最边上的位置,而是处于中间的位置。
获取中间元素的位置代码:
int GetMid(int* a, int left, int right)
{
int mid = left + right / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])
return left;
else
return right;
}
else
{
if (a[left] < a[right])
return left;
else if (a[mid] > a[right])
return mid;
else
return right;
}
}改进后的单趟排序代码:
int PartSort(int* a, int left, int right)
{
int mid = GetMid(a, left, right);
Swap(&a[mid], &a[left]);
int key = left;
while (left < right)
{
while (left < right && a[right]>=a[key])
{
right--;
}
while (left < right && a[left] <= a[key])
{
left++;
}
Swap(&a[right], &a[left]);
}
Swap(&a[left], &a[key]);
key = left;
return key;
}优化2:小区间优化法
我们再来看整个快速排序的整个递归过程,先对整个数组进行一次单趟排序,找到了一个key,此时key位置上的元素已经排好了序,所以就只需要再对key左边和右边的区间再次进行快速排序即可,一次快速排序就是一次递归调用,我们发现随着左右区间的缩小,递归的调用越来越多,特别是最后,调用的次数几乎占了所有的调用次数,为了避免递归深度太大,我们会将区间小于10的数组进行其它排序,我们这里建议用插入排序,因为插入排序的适用性好,所以改进后的代码如下:
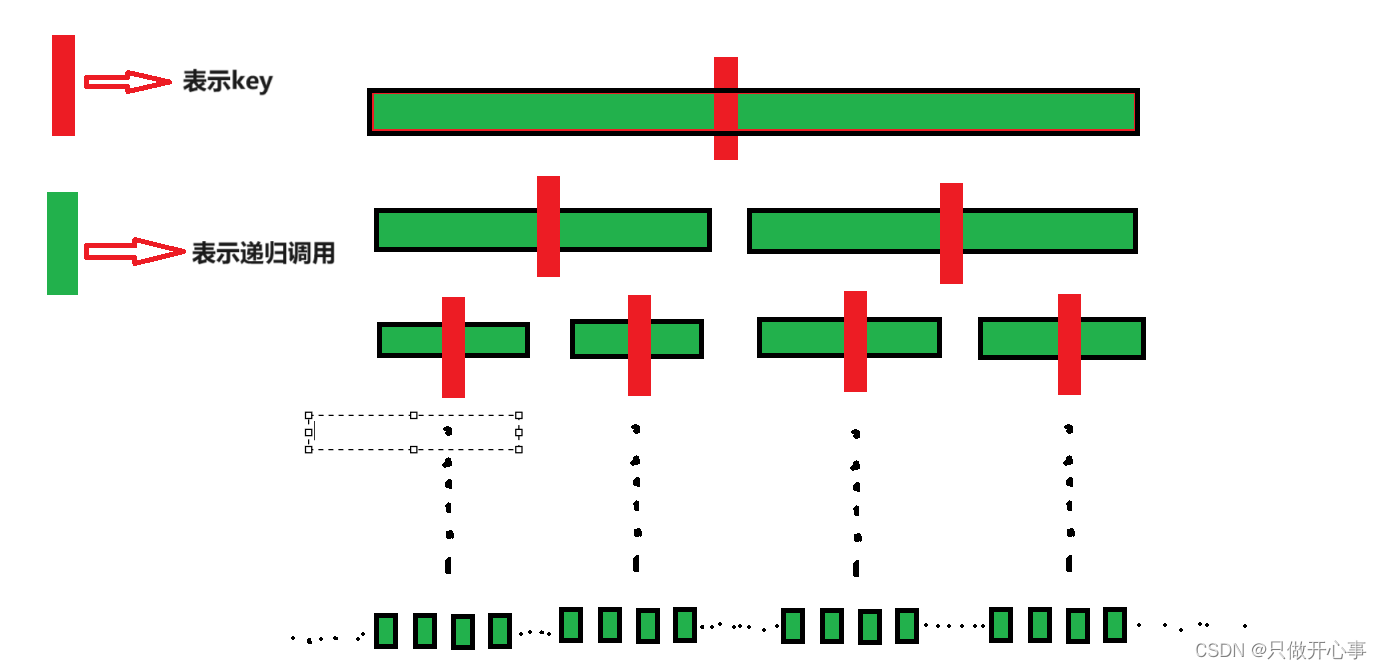
改进后快速排序的代码如下:
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
//小区间优化法
if (right - left+1 < 10)
{
InsertSort(a + left, right - left + 1);
}
int key= PartSort2(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
注意:小区间优化法所起的优化对比三数取中而言,优化的程度是很小的,因为三数取中完全是把快速排序最坏的场景硬生生的调整成了最好的场景,而三数取中则只是在最好的场景下,进行了部分优化,可以理解为雪中送炭和锦上添花的区别。
为了避免递归深度过深,我们不仅仅有三数取中法,还有非递归实现快速排序的方法,非递归实现快速排序我们下期会讲。
以上便是交换排序的所有内容,比较重要的还得是快速排序,所以一定要掌握。快速排序的非递归我们下期再讨论,欲知后事如何,且看下期分解。
本期的所有内容到此结束^_^