协方差矩阵的性质

• 实对称矩阵（第$i$元素和第$j$元素的耦合与第$j$元素和第$i$元素的耦合相等）
• Eigenvalues & eigenvecters (本征值, 本征向量)

$$\Sigma {\varphi }_i={\lambda }_i{\varphi }_i\Phi =\left[{\varphi }_1{\varphi }_2\cdots {\varphi }_d\right]\Lambda =\mathrm{diag}\left[{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_d\right]$$

• 特征向量的标准正交性
  $$\begin{array}{rl}& {\Phi }^T\Phi =I\\ & {\Phi }^T={\Phi }^{-1}\end{array}⟺{\varphi }_i^t{\varphi }_j=\{\begin{array}{ll}1,& i=j\\ 0,& i\ne j\end{array}$$
• 用矩阵的形式表示（有点绕，联系前面的符号定义进行理解）
  $$\Sigma \Phi =\Phi \Lambda \leftrightarrow \Sigma =\Phi \Lambda {\Phi }^T\leftrightarrow \Sigma =\sum _{i=1}^d{\lambda }_i{\varphi }_i{\varphi }_i^T$$
• 矩阵对角化
  $${\Phi }^T\Sigma \Phi =\Lambda =\left[\begin{array}{cccc}{\lambda }_1& 0& \dots & 0\\ 0& {\lambda }_2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\lambda }_d\end{array}\right]⟺{\varphi }_i^T\Sigma {\varphi }_i={\lambda }_i$$

Principal Component Analysis(PCA)

• 一种降维（特征提取）方法
• 将随机矢量投影到低维子空间，使子空间投影的重建误差最小
• 选择本征值最大的 $m(m<d)$ 个本征向量作为子空间的基(basis)

【证明】

• 线性空间中正交变换 $\left({\Phi }^T\Phi =I\right)$ 不影响欧氏距离(样本是$d$维的)
  $$\sum _{j=1}^d{\left[(\mathbf{x}-\mu {)}^T{\varphi }_j\right]}^2=\Vert \mathbf{x}-\mu {\Vert }^2$$
• 子空间投影（只取了$m$维）
  $$\mu +\sum _{j=1}^m\left[(\mathbf{x}-\mu {)}^T{\varphi }_j\right]{\varphi }_j$$
• 投影重建误差
  $$r_E=\Vert \mathbf{x}-\mu {\Vert }^2-\sum _{j=1}^m{\left[(\mathbf{x}-\mu {)}^T{\varphi }_j\right]}^2=\sum _{j=m+1}^d{\left[(\mathbf{x}-\mu {)}^T{\varphi }_j\right]}^2$$
• 重建误差的期望
  $$\begin{array}{rl}& \mathcal{E}\left(r_E\right)=\mathcal{E}\left\{\sum _{j=m+1}^d{\left[(\mathbf{x}-\mu {)}^T{\varphi }_j\right]}^2\right\}=\mathcal{E}\left\{\sum _{j=m+1}^d{\varphi }_j^T(\mathbf{x}-\mu )(\mathbf{x}-\mu {)}^T{\varphi }_j\right\}\\ & =\sum _{j=m+1}^d{\varphi }_j^T\mathcal{E}\left[(\mathbf{x}-\mu )(\mathbf{x}-\mu {)}^T\right]{\varphi }_j=\sum _{j=m+1}^d{\varphi }_j^T\Sigma {\varphi }_j=\sum _{j=m+1}^d{\lambda }_j\\ & \end{array}$$
• 对上式取最小就意味着取${\lambda }_i$最大的$m$个本征向量作为子空间基
  

线性变换的高斯分布

• 对于一个线性变换：$\mathbf{y}={\mathbf{A}}^t\mathbf{x}$
• 如果${\mathrm{A}}^{\mathrm{t}}\mathrm{A}=1$，叫做正交变换，相当于进行了旋转
• 高斯分布经过线性变换后还是高斯分布：$p(\mathbf{y})\sim N\left({\mathbf{A}}^t\mathbf{\mu },{\mathbf{A}}^t\mathbf{\Sigma }\mathbf{A}\right)$
• 如果变换矩阵是特征向量矩阵$A=\Phi$，那么变换后的高斯分布的协方差矩阵是对角矩阵$A^t\sum A=\Lambda$
• 白化变换（whitening transform）:更特别的，如果构造${\mathbf{A}}_w=\mathbf{\Phi }{\mathbf{\Lambda }}^{-1/2}$，那么变换后的高斯分布的协方差矩阵是单位矩阵
  $$\begin{array}{rl}& A_w^t\Sigma A_w={\Lambda }^{-1/2}{\Phi }^t\Sigma \Phi {\Lambda }^{-1/2}={\Lambda }^{-1/2}\Lambda {\Lambda }^{-1/2}=I\end{array}$$

高斯密度下的判别函数

• 判别函数
  $$g_i(\mathbf{x})=\ln p\left(\mathbf{x}\mid {\omega }_i\right)+\ln P\left({\omega }_i\right)$$
  回忆一下多变量高斯概率密度函数：
  $$p\left(\mathbf{x}\mid {\omega }_i\right)=\frac{1}{(2\pi {)}^{d/2}{\left|{\Sigma }_i\right|}^{1/2}}\exp \left[-\frac{1}{2}{\left(\mathbf{x}-{\mu }_i\right)}^t{\Sigma }_i^{-1}\left(\mathbf{x}-{\mu }_i\right)\right]$$
  于是
  $$g_i(\mathbf{x})=-\frac{1}{2}{\left(\mathbf{x}-{\mathbf{\mu }}_i\right)}^t{\mathbf{\Sigma }}_i^{-1}\left(\mathbf{x}-{\mathbf{\mu }}_i\right)-\frac{d}{2}\ln 2\pi -\frac{1}{2}\ln \left|{\Sigma }_i\right|+\ln P\left({\omega }_i\right)$$

下面对不同的协方差矩阵进行讨论，介绍两种特例

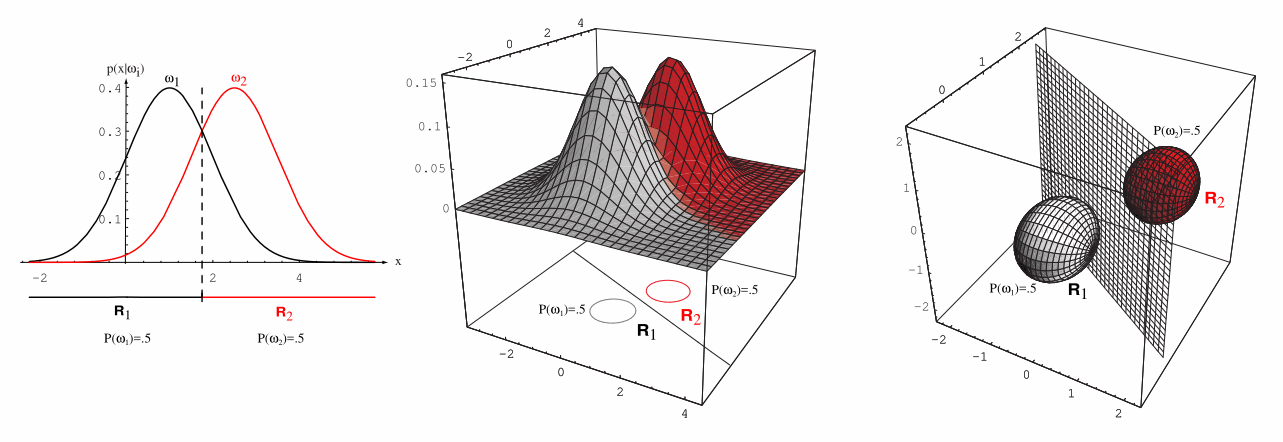
• 若${\Sigma }_i={\sigma }^{2}I$，则舍去与类别无关的常数项后，
  $$g_i(\mathrm{x})=-\frac{{\Vert \mathrm{x}-{\mathbf{\mu }}_i\Vert }^2}{2{\sigma }^2}+\ln P\left({\omega }_i\right)$$
  若${\Vert \mathrm{x}-{\mathbf{\mu }}_i\Vert }^2={\left(\mathrm{x}-{\mathbf{\mu }}_i\right)}^t\left(\mathrm{x}-{\mathbf{\mu }}_i\right)$，则
  $$g_i(\mathrm{x})=-\frac{1}{2{\sigma }^2}\left[{\mathrm{x}}^t\mathrm{x}-2{\mu }_i^t\mathrm{x}+{\mu }_i^t{\mu }_i\right]+\ln P\left({\omega }_i\right)$$
  再次舍去与类别无关常数项，得到最终的判别函数
  $$\begin{array}{rl}& g_i(\mathrm{x})={\mathbf{w}}_i^t\mathrm{x}+w_{i0}\\ & {\mathbf{w}}_i=\frac{1}{{\sigma }^2}{\mathbf{\mu }}_{\mathbf{i}}{w}_{i0}=\frac{-1}{2{\sigma }^2}{{\mathbf{\mu }}_{\mathbf{i}}}^t{\mathbf{\mu }}_i+\ln P\left({\omega }_i\right)\end{array}$$
  如果只有两类：
  $$\begin{array}{c}{g}_i(\mathrm{x})=g_j(\mathrm{x})\\ {\mathrm{w}}^t\left(\mathrm{x}-{\mathrm{x}}_0\right)=0\mathbf{w}={\mathbf{\mu }}_i-{\mathbf{\mu }}_j\\ {\mathrm{x}}_0=\frac{1}{2}\left({\mathbf{\mu }}_i+{\mathbf{\mu }}_j\right)-\frac{{\sigma }^2}{{\Vert {\mathbf{\mu }}_i-{\mathbf{\mu }}_j\Vert }^2}\ln \frac{P\left({\omega }_i\right)}{P\left({\omega }_j\right)}\left({\mathbf{\mu }}_i-{\mathbf{\mu }}_j\right)\end{array}$$
  如果两类先验概率相等，分界面就是两类均值连线的垂直平分面
  
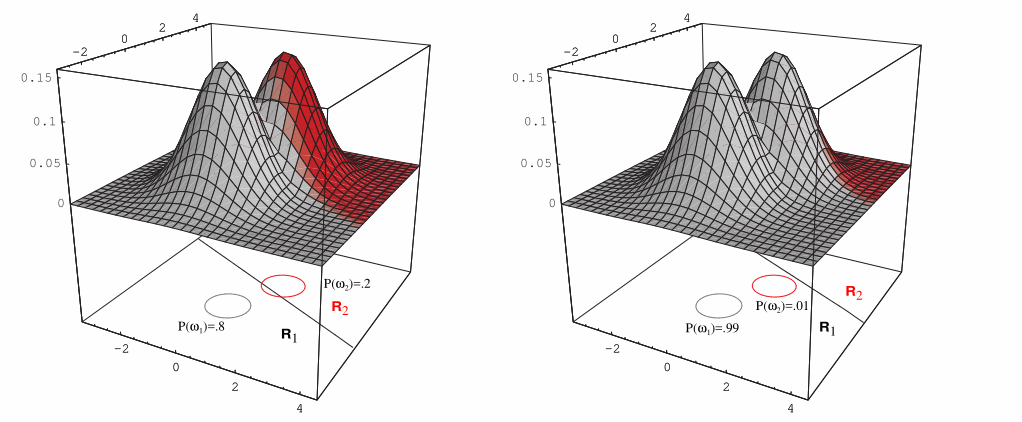
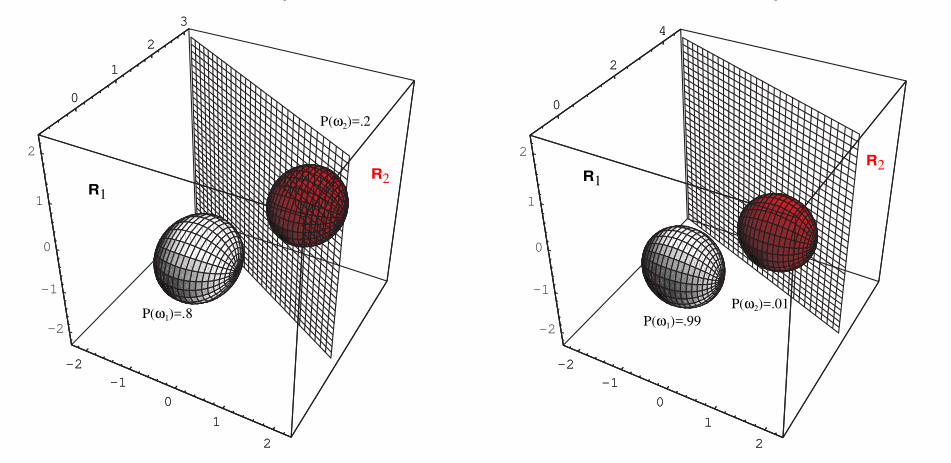
• 若${\Sigma }_i=\Sigma$，即所有类别的协方差矩阵都相等
  $$\begin{array}{c}{g}_i(\mathbf{x})=-\frac{1}{2}{\left(\mathbf{x}-{\mathbf{\mu }}_i\right)}^t{\mathbf{\Sigma }}_i^{-1}\left(\mathbf{x}-{\mathbf{\mu }}_i\right)-\frac{d}{2}\ln 2\pi -\frac{1}{2}\ln \left|{\mathbf{\Sigma }}_i\right|+\ln P\left({\omega }_i\right)\\ ⟹g_i(\mathbf{x})=-\frac{1}{2}{\left(\mathbf{x}-{\mathbf{\mu }}_i\right)}^t{\mathbf{\Sigma }}^{-1}\left(\mathbf{x}-{\mathbf{\mu }}_i\right)+\ln P\left({\omega }_i\right)\end{array}$$
  最终得到的线性判别函数是
  $$\begin{gathered} g_i(\mathbf{x})={\mathbf{w}}_i^t\mathbf{x}+w_{i0} \\ {\mathbf{w}}_i={\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_i{w}_{i0}=-\frac{1}{2}{\mathbf{\mu }}_i^t{\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_i+\ln P\left({\omega }_i\right) \end{gathered}$$
  如果只有两类
  $$\mathbf{w}={\Sigma }^{-1}\left({\mu }_i-{\mu }_j\right)$$
  $${\mathrm{x}}_0=\frac{1}{2}\left({\mathbf{\mu }}_i+{\mathbf{\mu }}_j\right)-\frac{\ln \left[P\left({\omega }_i\right)/P\left({\omega }_j\right)\right]}{{\left({\mathbf{\mu }}_i-{\mathbf{\mu }}_j\right)}^t{\mathbf{\Sigma }}^{-1}\left({\mathbf{\mu }}_i-{\mathbf{\mu }}_j\right)}\left({\mathbf{\mu }}_i-{\mathbf{\mu }}_j\right)$$
  如果两类的先验概率相等，那么分界面还是经过两类均值连线的中点，但不再垂直。