偏导数、雅克比矩阵、行列式都是非常重要的知识点,为了让大家更容易看懂,尽量使用画图来演示。
1、偏导数Partial derivative
对于导数我们已经很清楚了,某点求导就是某点的斜率,也就是这点的变化率。那么偏导数是什么,跟导数有什么不一样的地方,其实是一样的,只不过偏导是在多元(多个未知变量)的情况下,所以我们求导的时候,是偏向某个自变量求导,所以叫做偏导数(通俗解释,不严谨)。
百度百科的解释如下,一般都更偏向几何意义:
偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率;偏导数 f'y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。
高阶偏导数:如果二元函数 z=f(x,y) 的偏导数 f'x(x,y) 与 f'y(x,y) 仍然可导,那么这两个偏导函数的偏导数称为 z=f(x,y) 的二阶偏导数。二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy。
注意:
f"xy与f"yx的区别:前者是先对 x 求偏导,然后将所得的偏导函数再对 y 求偏导;后者是先对 y 求偏导再对 x 求偏导。当 f"xy 与 f"yx 都连续时,求导的结果与先后次序无关。
具体如何求,也是很简单的,我们只需要将需要求导的这个看作是自变量,其余的自变量都当成常数来对待就好了。
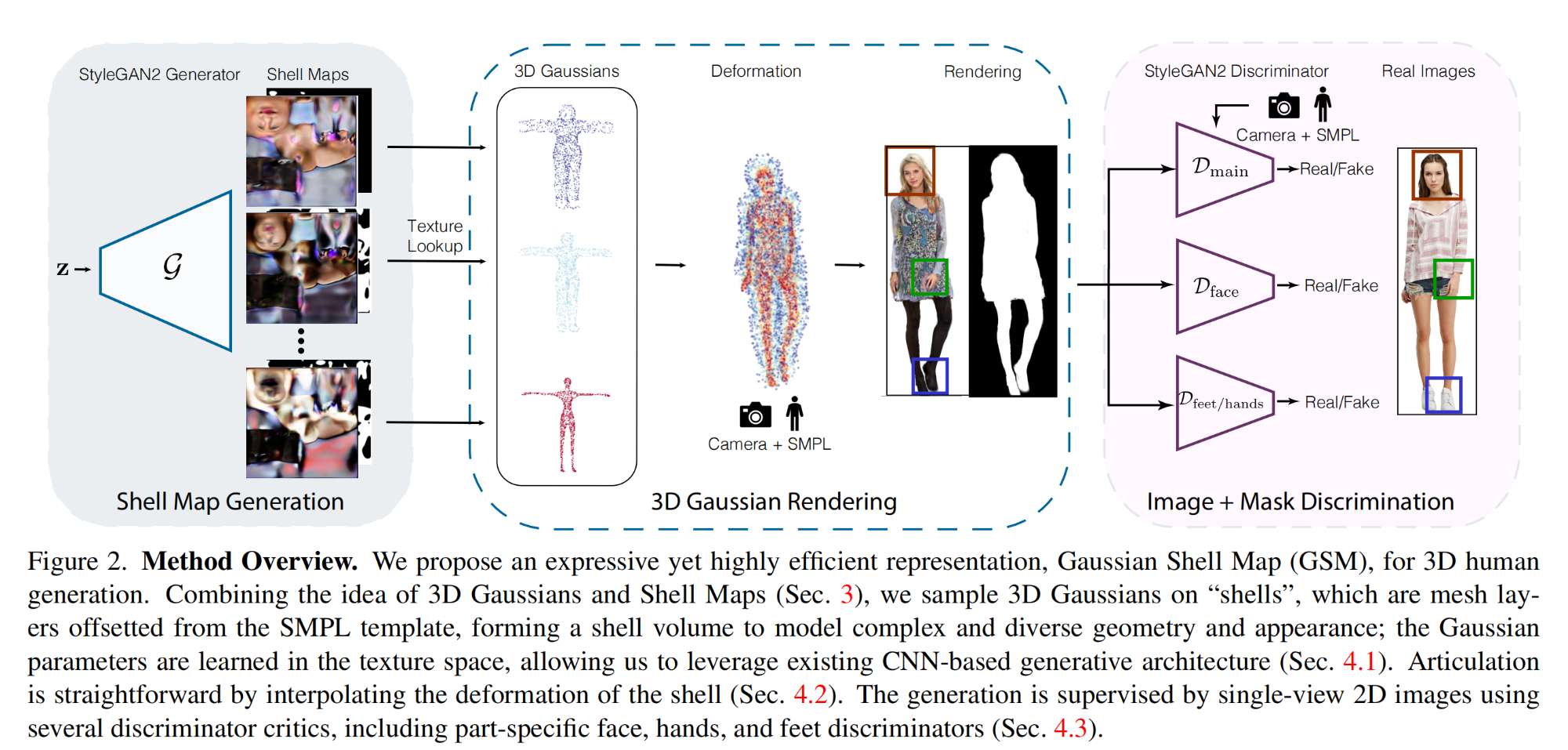
我们来看一张雅克比矩阵的图片,也是接下来需要讲的。

这张图虽然是雅克比矩阵,实质是求的偏导数,J(x)这个雅克比矩阵里面的值是怎么来的呢?我们看到红色圈起来的变量,也就是说在求这个偏导数的时候,我们将其余的变量都当作常量,比如说这个函数,如果求
的偏导数,那么可以看成是
,所以它的偏导数分别是2、
(看成是常数)、0(常数的导数是0),所以就是
,其余变量求偏导,同样的道理,将其他变量看成是常数来求即可。
2、雅克比矩阵Jacobian Matrix
掌握了上面介绍的偏导数,其实就明白了雅克比矩阵。
在向量微积分中,雅可比(Jacobian)矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。在人工智能领域,像这样的一阶偏导的集合,叫做梯度,这个概念非常非常重要,也是AI的核心之一。我们通过机器人的实践,更要明白其产生的意义是什么。
我们依然使用p560六自由度的机械臂为例,首先将机器人加载进来
startup_rvc
mdl_puma560
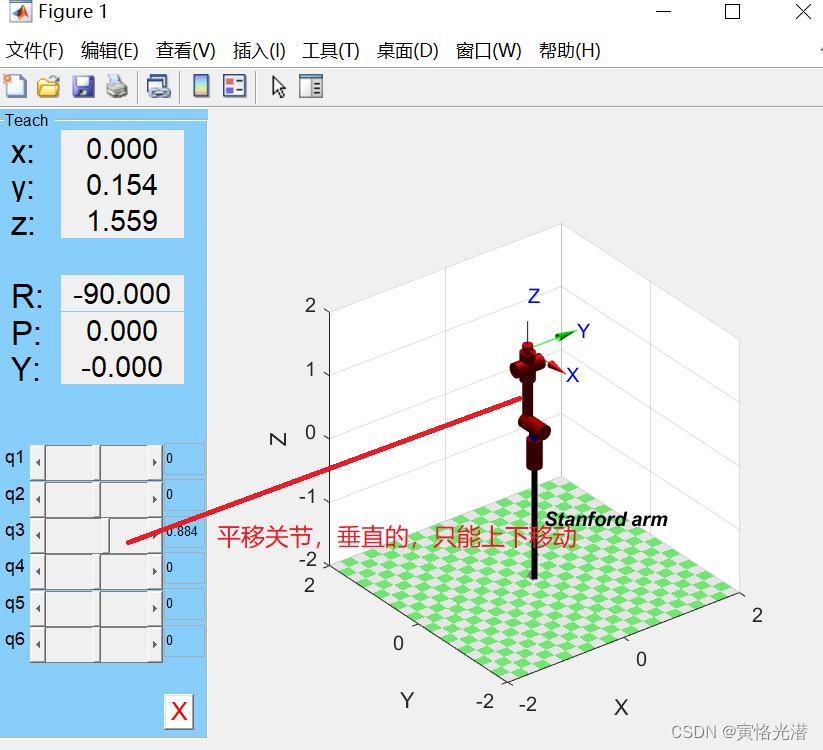
p560.teach当然还有其他自带的,如斯坦福机器人,sawyer机器人:
mdl_stanford
stanf.teach当然这个斯坦福机器人不是6个关节都可以旋转,其中有一个关节Prismatic只能平移
stanf.links
ans =
Revolute(std): theta=q1 d=0.412 a=0 alpha=-1.571 offset=0
Revolute(std): theta=q2 d=0.154 a=0 alpha=1.571 offset=0
Prismatic(std): theta=-1.571 d=q3 a=0 alpha=0 offset=0
Revolute(std): theta=q4 d=0 a=0 alpha=-1.571 offset=0
Revolute(std): theta=q5 d=0 a=0 alpha=1.571 offset=0
Revolute(std): theta=q6 d=0 a=0 alpha=0 offset=0
如下图:
mdl_sawyer
sawyer.teach这是一个7关节的机器人,每个关节Revolute都是可以旋转的:
ans =
Revolute(std): theta=q1 d=0.081 a=0.317 alpha=-1.571 offset=0
Revolute(std): theta=q2 d=0 a=0.1925 alpha=-1.571 offset=0
Revolute(std): theta=q3 d=0 a=0.4 alpha=-1.571 offset=0
Revolute(std): theta=q4 d=0 a=0.1685 alpha=-1.571 offset=0
Revolute(std): theta=q5 d=0 a=0.4 alpha=-1.571 offset=0
Revolute(std): theta=q6 d=0 a=0.1363 alpha=-1.571 offset=0
Revolute(std): theta=q7 d=0 a=0.1338 alpha=0 offset=0
如下图: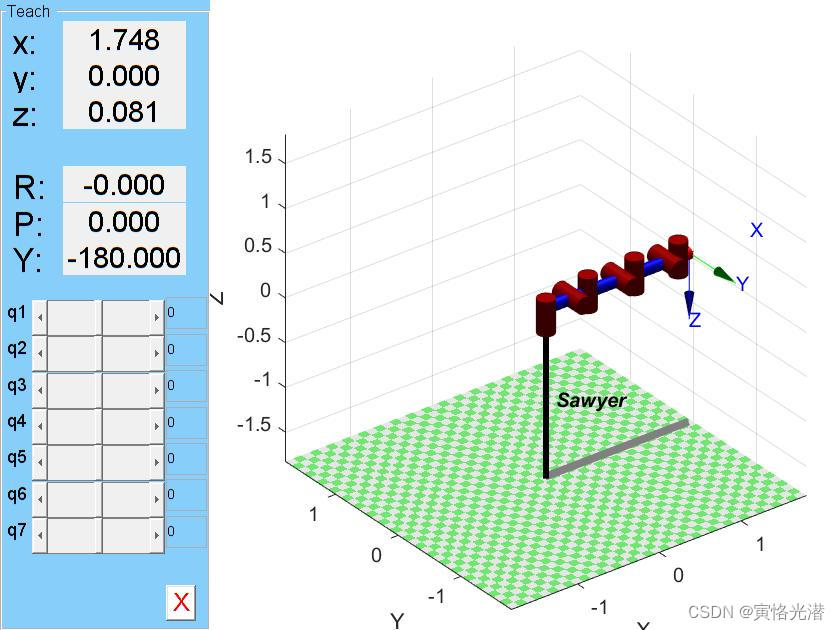 我们分别从世界坐标系和末端执行器坐标系来了解。
我们分别从世界坐标系和末端执行器坐标系来了解。
这个世界坐标系是机器人的参考坐标系,是用来描述机器人在整个运动区域的定位的。
我们使用标准状态来测试:qn[0 0.7854 3.1416 0 0.7854 0]
2.1、世界坐标系
我们来看下世界坐标系的雅克比矩阵,使用的是jacob0函数
J0n = p560.jacob0(qn)
J0n =
0.1501 0.0144 0.3197 0 0 0
0.5963 0.0000 0.0000 0 0 0
0.0000 0.5963 0.2910 0 0 0
-0.0000 0 0 0.7071 0 1.0000
-0.0000 -1.0000 -1.0000 -0.0000 -1.0000 -0.0000
1.0000 0.0000 0.0000 -0.7071 0.0000 -0.00002.2、末端执行器
接着来看下末端执行器的雅克比矩阵,平常经常说的末端执行器是一些吸盘、抓手、夹持器之类的设备,使用的是jacobe函数
JEn = p560.jacobe(qn)
JEn =
-0.0000 -0.5963 -0.2910 0 0 0
0.5963 0.0000 0.0000 0 0 0
0.1500 0.0144 0.3197 0 0 0
-1.0000 0 0 0.7071 0 0
-0.0000 -1.0000 -1.0000 -0.0000 -1.0000 0
-0.0000 0.0000 0.0000 0.7071 0.0000 1.0000可以看到机器人生成的雅克比矩阵是6x6的形状,前面也介绍了,因为行数是XYZRPY所以为6,又因为我们这里使用的是6自由度的机械臂,是6个关节,看做是6个自变量,所以列数是6。
另外我们可以看到右块的XYZ轴全部为零,这表明4、5、6三个关节的运动不会引起机器人末端执行器的任何平移运动,因为手腕关节是旋转的。
雅克比矩阵主要是用来求末端执行器的速度,而我们知道速度是位移的变化率,或者说是位移的导数(这里是偏导),这样是不是就跟上面的偏导数又结合起来了。
速度=雅克比矩阵与关节向量的点积。V=JEn*qn' (注意,qn需要做转置,不然前面矩阵列数与后面矩阵行数不一样)
V' :[-1.3825 0.0000 1.0156 0 -4.7124 0.0000]
3、行列式Determinant
行列式是对矩阵按一定规则进行运算之后得到的一个数值。行列式可以确定出对应矩阵是否存在着逆,即确定矩阵的奇异性,可以用来解线性方程组等。当行列式为0或近似于0时,其对应逆矩阵不存在,或虽然存在,但计算机计算出来的结果不正确。
我们来看下上面的雅可比矩阵的行列式: det(J0n)和det(JEn)都是-0.0786,不是0,所以可逆,inv(J0n)和inv(JEn)
我们自定义几个矩阵来具体看下这个行列式是怎么求值的,以及有什么意义。
mat0 = [3 0;0 2]
det(mat0)
%结果为6
mat1 = [1 2 3;4 5 6;7 8 9]
mat1 =
1 2 3
4 5 6
7 8 9
det(mat1)
%结果为-9.5162e-16 近似为0了,这里我们等会手动计算就是0,所以不可逆,或者结果不正确我们来看下它的逆矩阵:
inv(mat1)警告: 矩阵接近奇异值,或者缩放错误。结果可能不准确。RCOND = 2.202823e-18。
我们将矩阵修改下
mat2 = [1 2 3;4 5 6;7 8 0]然后求行列式:det(mat2)结果为27.0000,好的,不是0的情况,就可逆inv(mat2)
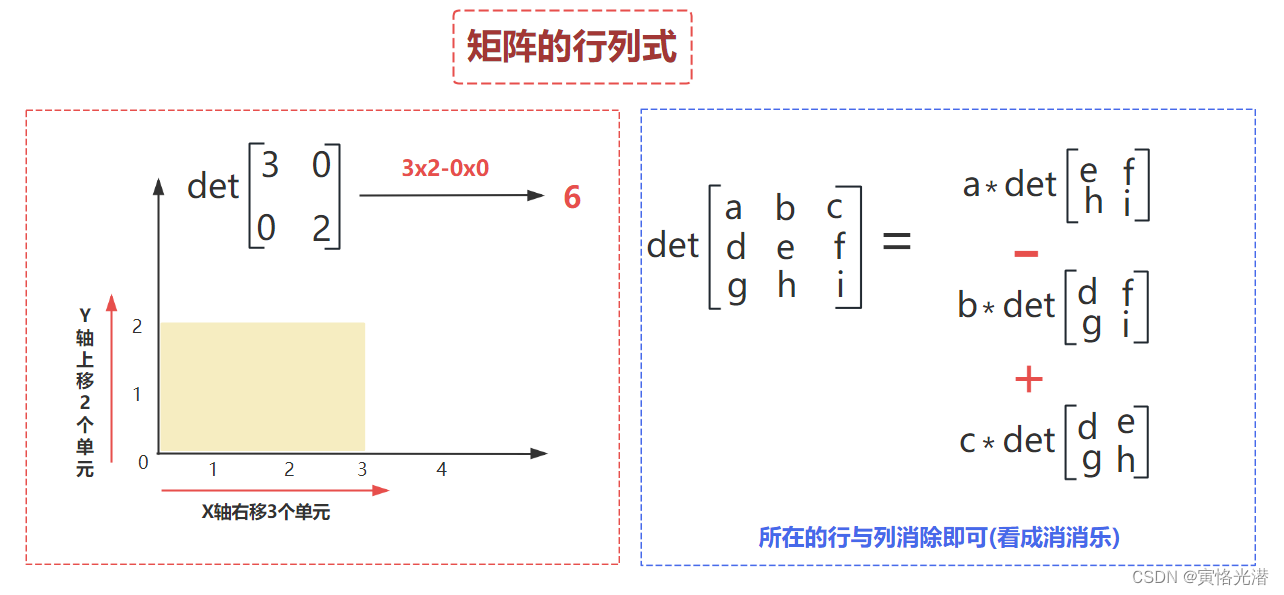
那么这些值是怎么算出来的呢?依然通过画图来给大家直观感受下:
 4、行列式推导
4、行列式推导
从错误提示以及图片,我们可以看到行列式,其实是在做拉伸或叫缩放的操作,mat0的矩阵的行列式我们可以知道是面积放大了6倍,这个就是行列式的几何意义。
对于这个矩阵的行列式是具体如何计算得到的,我们一起来看下推导过程:
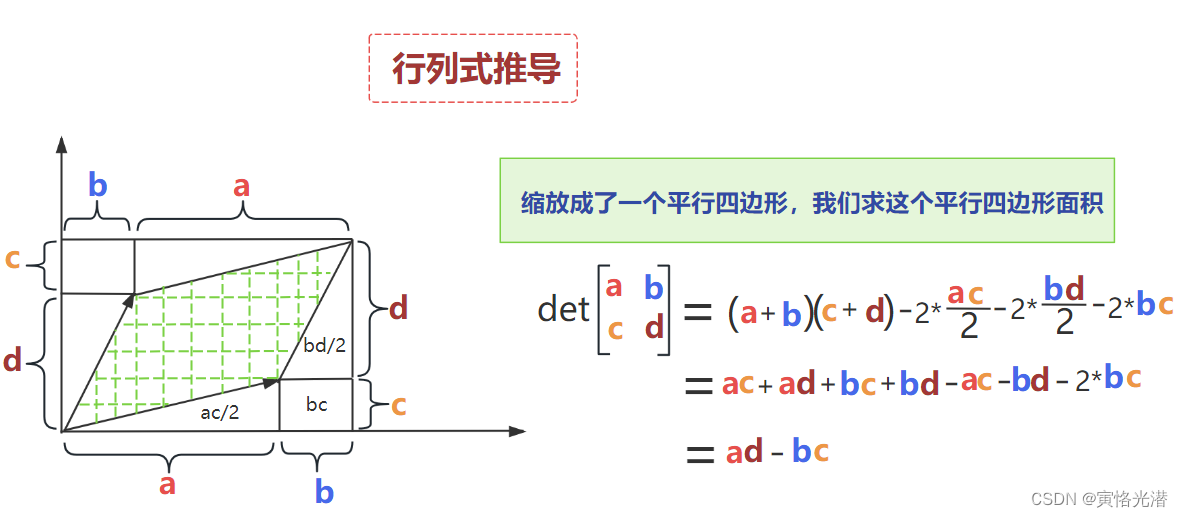
我们实际是求这个缩放的平行四边形的面积,如果求出来的结果是0,这种情况我们前面也验证过,这个矩阵是不可逆,这个通俗来说就是降维了,就类似于“万向节死锁”的现象出现了,成为了线性关系,所以不能反推回去,有兴趣的可以点击:欧拉角(横滚角、俯仰角、偏航角)、旋转矩阵、四元数的转换与解决万向节死锁