学习目标:
动态规划五部曲:
① 确定dp[i]的含义
② 求递推公式
③ dp数组如何初始化
④ 确定遍历顺序
⑤ 打印递归数组 ---- 调试
引用自代码随想录!
60天训练营打卡计划!
学习内容:
完全背包问题 – 二维dp数组
- 动态规划五步曲:
① 确定dp[i][j]的含义 : 任取[0, i]的物品(可重复使用)后放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[i][j] = Math.max(dp[i-1][j], dp[i][j-weight[i]] + value[i]);
Ⅰ 不放物品 i : dp[i][j] = dp[i-1][j];
Ⅱ 放物品 i : dp[i][j-weight[i]] + value[i] 依赖本行已填充的值
③ dp数组如何初始化 : 对第一行进行单独的初始化,如下图所示。当背包容量大于第一个物品的重量时开始放入背包,一直连续放入。
④ 遍历顺序:先遍历物品,再遍历背包,和01背包问题一致。
下面的代码应该是没问题的,但是数字量变大之后会很容易超时。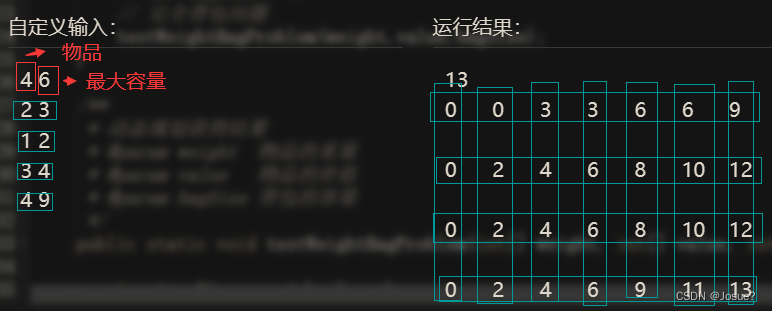
// 动态规划
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
//m,n分别代表物品种类和背包容量
int itemSize = 0,bagSize = 0;
Scanner sc = new Scanner(System.in);
//获取itemSize和bagSize的值
itemSize = sc.nextInt();
bagSize = sc.nextInt();
//初始化对应的重量数组和价值数组
int[] weight = new int[itemSize];
int[] value = new int[itemSize];
//这两个都是物品的属性,大小只和物品数量有关
for(int i = 0;i < itemSize;i++){
weight[i] = sc.nextInt();
value[i] = sc.nextInt();
}
// 完全背包问题
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
int itemSize = weight.length;
// dp数组的含义是:在[0,i]件物品中选择是否放入背包 的 最大价值
int[][] dp = new int[itemSize][bagSize+1];
int val = 0;
// 初始化dp数组,默认都为0.
// 使用最小重量的物品为该物品所在行赋值
for(int j = weight[0]; j < bagSize+1; j++){
if(j % weight[0] == 0) val += value[0];
dp[0][j] = val;
}
// 正常的为dp数组赋值,依赖左上位置的其他的dp值
for(int i = 1; i < itemSize; i++){
// j是背包容量
for(int j = 1; j < bagSize+1; j++){
// 如果容量可以放入新的物品,则从本行的左侧继承
if(j >= weight[i]){
// 一定要填j < weight[i]的位置,
// dp[i][j-weight[i]]与该行左侧的值息息相关。
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-weight[i]] + value[i]);
}
// 如果容量不够放入新的物品,则从上一行继承
else if(j < weight[i]) dp[i][j] = dp[i-1][j];
}
}
System.out.println(dp[itemSize-1][bagSize]);
// 打印dp数组
for (int i = 0; i < itemSize; i++) {
for (int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + "\t");
}
System.out.println("\n");
}
}
}
完全背包问题 – 一维dp数组
- 动态规划五步曲:
① 确定dp[j]的含义 : 任取[0, i]的物品(可重复使用)后放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[j] = Math.max(dp[j], dp[j-weight[i]] + value[i]);
Ⅰ 不放物品 i : dp[j]
Ⅱ 放物品 i : dp[j-weight[i]] + value[i]
③ dp数组如何初始化 : 初始化为0
④ 遍历顺序:先遍历物品,再遍历背包(正序),和01背包问题8同。
虽然下面的代码应该是没问题的,但是数字量变大之后会很容易超时。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
//m,n分别代表物品种类和背包容量
int itemSize = 0,bagSize = 0;
Scanner sc = new Scanner(System.in);
//获取itemSize和bagSize的值
itemSize = sc.nextInt();
bagSize = sc.nextInt();
//初始化对应的重量数组和价值数组
int[] weight = new int[itemSize];
int[] value = new int[itemSize];
//这两个都是物品的属性,大小只和物品数量有关
for(int i = 0;i < itemSize;i++){
weight[i] = sc.nextInt();
value[i] = sc.nextInt();
}
// 完全背包问题
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
int itemSize = value.length;
int[] dp = new int[bagSize+1];
// 初始化为0
// 递归推导
for(int i = 0; i < itemSize; i++){
for(int j = weight[i]; j < bagSize+1; j++){
dp[j] = Math.max(dp[j], dp[j-weight[i]] + value[i]);
// System.out.print(dp[j] + "\t");
}
// System.out.println("\n");
}
System.out.print(dp[bagSize] + "\n");
}
}
518.零钱兑换II
- 动态规划五步曲:
① 确定dp[i]的含义 : 装满容量为i的背包有dp[i]种方法。
② 求递推公式 : dp[j] += dp[j - coins[i]] (装满背包的方法数的相关问题的统一递归公式)
③ dp数组如何初始化 : dp[0] = 1 (若dp[0] = 0,则所有的全部为0。)
④ 确定遍历顺序 : 从前向后,先物品后背包
⑤ 打印dp数组
组合的dp数组
1 1 1 1 1
1 2 2 3 3
1 2 2 3 4
排列的dp数组
1 1 1
1 1 1
1 2 2
2 3 3
3 5 5
5 8 9
- 一种记忆方法:先遍历物品(物品不会重复被取得)为组合
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
int itemSize = coins.length;
// 初始化
dp[0] = 1;
// 递归推导
for(int i = 0; i < itemSize; i++){
// 先物品后背包就可以保证是组合而不是排列
for(int j = coins[i]; j < amount+1; j++){
// 因为减去coins[i]的面值,就是可以凑出的方法数。
dp[j] += dp[j - coins[i]];
System.out.println(dp[j]);
}
System.out.println("*");
}
// for(int j = 0; j < amount+1; j++){
// // 先背包后物品就可以保证是排列而不是组合
// // for(int j = i; j < amount+1; j++){
// for(int i = 0; i < itemSize; i++){
// // 因为减去coins[i]的面值,就是可以凑出的方法数。
// if(j - coins[i] >= 0)
// dp[j] += dp[j - coins[i]];
// System.out.println(dp[j]);
// }
// System.out.println("*");
// }
return dp[amount];
}
}
377.组合总和IV
- 动态规划五步曲:
① 确定dp[i]的含义 : 装满容量为i的背包有dp[i]种方法(排列)。
② 求递推公式 : dp[j] += dp[j - coins[i]] (装满背包的方法数的相关问题的统一递归公式)
③ dp数组如何初始化 : dp[0] = 1 (若dp[0] = 0,则所有的全部为0。)
④ 确定遍历顺序 : 从前向后,先背包后物品
⑤ 打印dp数组
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
int itemSize = nums.length;
Arrays.sort(nums);
// 初始化
dp[0] = 1;
// 递归推导
for(int j = 0; j < target+1; j++){
// 先背包后物品就可以保证是排列而不是组合
for(int i = 0; i < itemSize && j >= nums[i] ; i++){
// 因为减去coins[i]的面值,就是可以凑出的方法数。
dp[j] += dp[j - nums[i]];
// System.out.println(dp[j]);
}
// System.out.println("*");
}
return dp[target];
}
}
学习时间:
- 上午两个半小时,整理文档半小时。



![2024 年 20 款最佳免费视频转换器软件 [安全快速有效]](https://img-blog.csdnimg.cn/direct/8255d258c123470695edfec2abfd2983.png)