【数据结构】—红黑树（C++实现）

news2024/11/28 21:38:12

                                                       🎬慕斯主页：修仙—别有洞天

                                                 💜本文前置知识： AVL树

                                                      ♈️今日夜电波：Letter Song—ヲタみん

                                                                1:36━━━━━━️💟──────── 5:35
                                                                    🔄   ◀️   ⏸   ▶️    ☰  

                                      💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍

目录

一、前言  

        红黑树的概念 

        红黑树与二叉搜索树的异同

二、红黑树的实现

        节点的定义

        AVL树的初始化定义

红黑树的插入（重点及难点！！！） 

        插入大致步骤

        插入的总体逻辑 

        按照二叉搜索树的方法插入节点

        父节点为红色， 需要进行相应的调整

        情况一: cur为红，p为红，g为黑，u存在且为红

        情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑​编辑

        情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

        插入实现 

        根据构建红黑树的规则验证红黑树

        求红黑树高度以及遍历红黑树

三、总体代码

一、前言  

         本文是基于二叉搜索树以及AVL树的知识前提下对于红黑树进行叙述的，主要叙述的方面同AVL树一样，主要是在于插入方面的解析，其它部分同AVL树和二叉搜索树还是有些相似的。但是对于删除部分来说，红黑树就太难了，举个例子？：插入部分，红黑树的实现大概180行代码，而删除则是400往上接近500行了。难度可想而知，作者如果有能力后续会慢慢补齐的！

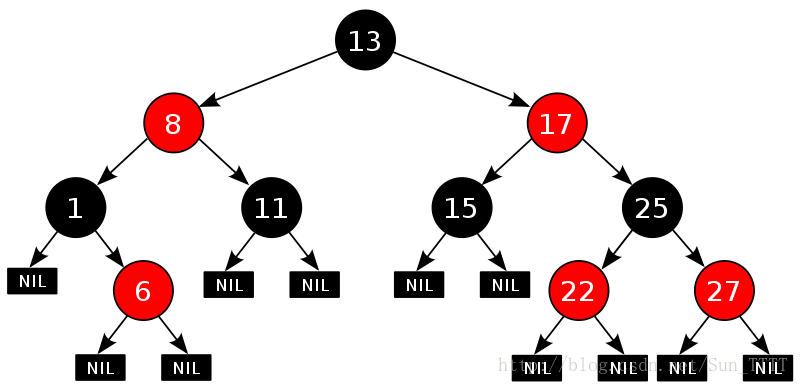
        红黑树的概念 

        红黑树是一种自平衡二叉查找树，它的每个节点都有一个颜色属性，可以是红色或黑色。红黑树的特性如下：

  • 每个节点要么是红色，要么是黑色。
  • 根节点是黑色。
  • 所有的叶子节点（NIL节点）都是黑色。（注意NIL实际上空节点，只不过我们将所有空节点看作黑色节点而已）
  • 如果一个节点是红色，那么它的两个子节点都是黑色。（意味着黑色可以有黑色的节点也可以有红色的节点，但是红色只能有黑色的节点）
  • 对于每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

        这些特性保证了红黑树的搜索效率。在最坏的情况下，搜索一棵高度为h的红黑树的时间复杂度是O(h)，与AVL树相当。此外，由于红黑树的插入和删除操作不需要像AVL树那样频繁地旋转，因此红黑树在实际应用中比AVL树更加稳定和高效。

在实际应用中，红黑树常用于实现关联数组（哈希表）的数据结构，以及数据库索引等场合。

        红黑树与二叉搜索树的异同

        红黑树和二叉搜索树的主要区别在于它们如何处理数据冲突。

        二叉搜索树（BST）是一种特殊的二叉树，其中每个节点都存储一个键值，并且满足左子树中的所有键值小于根节点的键值，右子树中的所有键值大于根节点的键值。这使得搜索、插入和删除操作可以在平均情况下以O(log n)的时间复杂度完成。

        红黑树也是一种二叉搜索树，但它通过限制每个节点的颜色和位置关系来保持树的平衡，从而确保搜索、插入和删除操作的时间复杂度始终为O(log n)。与BST不同的是，红黑树还具有以下特点：

  * 每个节点要么是红色，要么是黑色。
  * 根节点是黑色。
  * 所有的叶子节点（NIL节点，空节点）都是黑色。
  * 如果一个节点是红色，那么它的两个子节点都是黑色。
  * 对于每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

        这些特性使得红黑树在实际应用中更加强大和灵活。例如，红黑树可以通过左右旋转变换快速调整树的形状，从而应对动态数据集的变化。此外，红黑树还可以应用于许多不同的场景，如数据库索引、排序算法、集合类数据结构等等。

二、红黑树的实现

         节点的定义

         使用枚举来定义结点的颜色，提高代码的可读性。定义三叉链，方便后续的旋转等等操作，定义KV结构的红黑树，定义一个枚举变量用于储存颜色。通过构造函数初始化节点。

enum Color
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;

	pair<K, V> _kv;
	Color _col;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};

        AVL树的初始化定义

template<class K, class V>
struct RBTree
{
	typedef RBTreeNode<K, V> Node;

public:

	bool Insert(const pair<K, V>& kv)//插入操作

	bool IsBalance();//判断是否符合红黑树

	int Height();//求高度

private:

	Node* _root = nullptr;//给缺省初始化

};

红黑树的插入（重点及难点！！！） 

         插入大致步骤

下面是红黑树插入的大致步骤：

1. 向红黑树中插入新的节点。

2. 确保新节点的颜色为红色。

3. 确保新插入的节点不会破坏红黑树的性质。如果新节点违反了某些性质，则需要对红黑树进行旋转操作或更改节点的颜色。

4. 返回到插入节点的父节点，继续执行第3步，直到所有违反性质的节点都被修复为止。

具体来说，当我们向红黑树中插入新的节点时，我们需要遵循以下规则：

        - 每个节点都是红色或黑色。

        - 根节点是黑色。

        - 所有叶子节点（NIL节点，空节点）都是黑色。

        - 如果一个节点是红色，则它的两个子节点都是黑色。

        - 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

        如果我们违反了这些规则中的任何一个，我们就可以通过旋转操作或更改节点的颜色来修复这个问题。例如，如果我们发现某个节点有两个子节点都是红色的，那么我们就需要将这个节点以及其两个子节点的颜色全部改为黑色，然后再将该节点的父节点变为红色。这样就可以确保新插入的节点不会破坏红黑树的性质。

        插入的总体逻辑 

  1. 按二叉搜索树的插入方法，找到待插入位置。
  2. 将待插入结点插入到树中。（新插入的节点默认为红）
  3. 若插入结点的父结点是红色的，则需要对红黑树进行调整。
  4. 按情况进行调整：情况一: cur为红，p为红，g为黑，u存在且为红。->将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑->p为g的左孩子，cur为p的左孩子，则进行右单旋转；相反， p为g的右孩子，cur为p的右孩子，则进行左单旋转p、g变色--p变黑，g变红。情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑->p为g的左孩子，cur为p的右孩子，则针对p做左单旋转，再对g做右单旋；相反， p为g的右孩子，cur为p的左孩子，则针对p做右单旋转，再对g做左单旋。

        按照二叉搜索树的方法插入节点

         按照搜索二叉树，大往右，小往左的思想，找到对应的节点，插入节点并且链接。大致步骤都是同二叉搜索树是相同的，只不过需要注意的是新插入的节点默认都是红色的。当父节点为黑色时，直接插入即可。

bool Insert(const pair<K, V>& kv)
{
	if (_root == nullptr)//如果根节点为空则直接开辟一个节点作为根节点并且返回true
	{
		_root = new Node(kv);
		_root->_col = BLACK;
		return true;
	}

	
	Node* parent = nullptr;//后续遍历找位置以及旋转等

	Node* cur = _root;//遍历用

	while (cur) // 开始遍历到指定位置->其实就是到cur为空节点的地方
	{
		if (cur->_kv.first < kv.first)//要插入节点大于则往右遍历
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)//要插入节点小于于则往左遍历
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	//默认新增节点给红色，防止给黑破坏平衡

	cur = new Node(kv);
	cur->_col = RED;

	if (parent->_kv.first < kv.first)//同父节点比大小
	{
		parent->_right = cur;//链接新节点
	}
	else
	{
		parent->_left = cur;//链接新节点
	}

	cur->_parent = parent;//新节点链接父节点

	//后续根据红黑树特性开始调整
	...
    
    //调整完毕
	}

	_root->_col = BLACK;//将根处理成黑。因为插入向上处理会改变，但是当最后为根时改变后就不能进入循环，因此需要最后处理为黑

	return true;
}

        父节点为红色， 需要进行相应的调整

        重点在于看舅舅节点，看舅舅节点的存在与否，存在的话是红色？还是黑色？ 根据舅舅节点来确定相应的调整操作。然后再看新插入节点cur处于parent的位置，在左？还是在右？进行相应的调整策略。

        情况一: cur为红，p为红，g为黑，u存在且为红

         当cur为红，p为红，g为黑，u存在且为红时，将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。

         情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

        当cur为红，p为红，g为黑，u不存在/u存在且为黑，u不存在，如果p为g的左，cur为p的左，如上图一所示，则只需对g进行右单旋，如果p为g的右，cur为p的右，则只需对g进行左单旋，然后p、g变色--p变黑，g变红。

        当u存在且为黑，即如上图二第2步所示。由图二1、2步我们可以知道cur是由于新增节点而变化而来的，我们也可以根据红黑树的定义可知，c、d、e分别为对应箭头的颜色。由此，我们需要进行对应的旋转以及变色操作，对于以上u存在且为黑，如果p为g的左，cur为p的左，则如图二第3步所示，对p进行右单旋，如果p为g的右，cur为p的右，则只需对g进行左单旋，然后p、g变色--p变黑，g变红。

         情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

        当cur为红，p为红，g为黑，u不存在/u存在且为黑，但是此时,如果p为g的左，cur为p的右，则如图所示需先对p进行左单旋，再对g进行右单旋。如果p为g的右，cur为p的左，则需对p进行右单旋，再对g进行左单旋。然后c、g变色--c变黑，g变红。 

        插入实现 

	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)//如果根节点为空则直接开辟一个节点作为根节点并且返回true
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		
		Node* parent = nullptr;//后续遍历找位置以及旋转等

		Node* cur = _root;//遍历用

		while (cur) // 开始遍历到指定位置->其实就是到cur为空节点的地方
		{
			if (cur->_kv.first < kv.first)//要插入节点大于则往右遍历
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)//要插入节点小于于则往左遍历
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		//默认新增节点给红色，防止给黑破坏平衡

		cur = new Node(kv);
		cur->_col = RED;

		if (parent->_kv.first < kv.first)//同父节点比大小
		{
			parent->_right = cur;//链接新节点
		}
		else
		{
			parent->_left = cur;//链接新节点
		}

		cur->_parent = parent;//新节点链接父节点

		//根据红黑树特性开始调整
		while (parent && parent->_col == RED)//由于子节点和父节点都是红色，则需要调整
		{
			Node* grandfather = parent->_parent;//储存爷爷节点，用于找舅舅节点以及变色甚至旋转
			if (parent == grandfather->_left)
			{
				//     g
				//   p   u
				// c
				Node* uncle = grandfather->_right;//如果父亲节点在爷爷的左则舅舅在右
				if (uncle && uncle->_col == RED)//情况一：“变色处理” 舅舅节点存在且为红色，则我们需要将父亲以及舅舅变黑，爷爷变红
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else //情况二：“需要旋转（单旋？or双旋？）+变色处理” 即舅舅节点存在时为黑或者舅舅节点不存在，则我们需要进行相应的旋转
				{
					if (cur == parent->_left)
					{
						// 单旋
						//     g         p  
						//   p     ->  c   g
						// c
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						// 双旋
						//     g          g        p  
						//   p     ->   c    ->  c   g
						//     c      p
						RotateL(parent);
						RotateR(grandfather);

						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else // parent == grandfather->_right
			{
				//     g
				//   u   p 
				//          c
				//
				Node* uncle = grandfather->_left;//情况一，但是uncle在左
				// u存在且为红
				if (uncle && uncle->_col == RED)
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else//情况二：“需要旋转（单旋？or双旋？）+变色处理”
				{
					if (cur == parent->_right)
					{
						// 单旋
						//     g           p  
						//       p   ->  g   c
						//         c
						RotateL(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else
					{
						//     g        g           c
						//   u   p -> u   c   ->  g   p
						//     c            p   u
						//
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;//将根处理成黑。因为插入向上处理会改变，但是当最后为根时改变后就不能进入循环，因此需要最后处理为黑

		return true;
	}

	void RotateL(Node* parent)
	{
		++_rotateCount;

		Node* cur = parent->_right;
		Node* curleft = cur->_left;

		parent->_right = curleft;
		if (curleft)
		{
			curleft->_parent = parent;
		}

		cur->_left = parent;

		Node* ppnode = parent->_parent;

		parent->_parent = cur;


		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;

			}

			cur->_parent = ppnode;
		}
	}


	void RotateR(Node* parent)
	{
		++_rotateCount;

		Node* cur = parent->_left;
		Node* curright = cur->_right;

		parent->_left = curright;
		if (curright)
			curright->_parent = parent;

		Node* ppnode = parent->_parent;
		cur->_right = parent;
		parent->_parent = cur;

		if (ppnode == nullptr)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}

			cur->_parent = ppnode;
		}
	}

         根据构建红黑树的规则验证红黑树

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
	bool IsBalance()
	{
		return _IsBalance(_root);
	}

	// 根节点->当前节点这条路径的黑色节点的数量
	bool CheckColour(Node* root, int blacknum, int benchmark)
	{
		if (root == nullptr)
		{
			if (blacknum != benchmark)
				return false;

			return true;
		}

		if (root->_col == BLACK)//统计黑色用于判断每条路径黑色都相同
		{
			++blacknum;
		}

		if (root->_col == RED && root->_parent && root->_parent->_col == RED)
		{
			//当前节点与父节点连续红色
			cout << root->_kv.first << "出现连续红色节点" << endl;
			return false;
		}

		return CheckColour(root->_left, blacknum, benchmark)
			&& CheckColour(root->_right, blacknum, benchmark);//递归遍历每条路径
	}

	bool _IsBalance(Node* root)
	{
		//根据构建红黑树的规则进行判断
		if (root == nullptr)
			return true;

		if (root->_col != BLACK)//根不能为红
		{
			return false;
		}

		// //参考值,统计一条路径的黑色节点数
		int benchmark = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				++benchmark;

			cur = cur->_left;
		}

		//通过检查每条路径的黑色节点数判断是否平衡
		return CheckColour(root, 0, benchmark);
	}

        求红黑树高度以及遍历红黑树

         基本上就是同AVL树以及搜索二叉树相同的道理。

	int Height()
	{
		return _Height(_root);
	}

	//中序遍历
	void Inorder()
	{
		_Inorder(_root);
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);

		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	//中序遍历子函数
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << " ";
		_Inorder(root->_right);
	}

三、总体代码

#pragma once
#include<iostream>
using namespace std;

enum Color
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;

	pair<K, V> _kv;
	Color _col;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};

template<class K, class V>
struct RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)//如果根节点为空则直接开辟一个节点作为根节点并且返回true
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		
		Node* parent = nullptr;//后续遍历找位置以及旋转等

		Node* cur = _root;//遍历用

		while (cur) // 开始遍历到指定位置->其实就是到cur为空节点的地方
		{
			if (cur->_kv.first < kv.first)//要插入节点大于则往右遍历
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)//要插入节点小于于则往左遍历
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		//默认新增节点给红色，防止给黑破坏平衡

		cur = new Node(kv);
		cur->_col = RED;

		if (parent->_kv.first < kv.first)//同父节点比大小
		{
			parent->_right = cur;//链接新节点
		}
		else
		{
			parent->_left = cur;//链接新节点
		}

		cur->_parent = parent;//新节点链接父节点

		//根据红黑树特性开始调整
		while (parent && parent->_col == RED)//由于子节点和父节点都是红色，则需要调整
		{
			Node* grandfather = parent->_parent;//储存爷爷节点，用于找舅舅节点以及变色甚至旋转
			if (parent == grandfather->_left)
			{
				//     g
				//   p   u
				// c
				Node* uncle = grandfather->_right;//如果父亲节点在爷爷的左则舅舅在右
				if (uncle && uncle->_col == RED)//情况一：“变色处理” 舅舅节点存在且为红色，则我们需要将父亲以及舅舅变黑，爷爷变红
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else //情况二：“需要旋转（单旋？or双旋？）+变色处理” 即舅舅节点存在时为黑或者舅舅节点不存在，则我们需要进行相应的旋转
				{
					if (cur == parent->_left)
					{
						// 单旋
						//     g         p  
						//   p     ->  c   g
						// c
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						// 双旋
						//     g          g        p  
						//   p     ->   c    ->  c   g
						//     c      p
						RotateL(parent);
						RotateR(grandfather);

						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else // parent == grandfather->_right
			{
				//     g
				//   u   p 
				//          c
				//
				Node* uncle = grandfather->_left;//情况一，但是uncle在左
				// u存在且为红
				if (uncle && uncle->_col == RED)
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else//情况二：“需要旋转（单旋？or双旋？）+变色处理”
				{
					if (cur == parent->_right)
					{
						// 单旋
						//     g           p  
						//       p   ->  g   c
						//         c
						RotateL(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else
					{
						//     g        g           c
						//   u   p -> u   c   ->  g   p
						//     c            p   u
						//
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;//将根处理成黑。因为插入向上处理会改变，但是当最后为根时改变后就不能进入循环，因此需要最后处理为黑

		return true;
	}

	void RotateL(Node* parent)
	{
		++_rotateCount;

		Node* cur = parent->_right;
		Node* curleft = cur->_left;

		parent->_right = curleft;
		if (curleft)
		{
			curleft->_parent = parent;
		}

		cur->_left = parent;

		Node* ppnode = parent->_parent;

		parent->_parent = cur;


		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;

			}

			cur->_parent = ppnode;
		}
	}


	void RotateR(Node* parent)
	{
		++_rotateCount;

		Node* cur = parent->_left;
		Node* curright = cur->_right;

		parent->_left = curright;
		if (curright)
			curright->_parent = parent;

		Node* ppnode = parent->_parent;
		cur->_right = parent;
		parent->_parent = cur;

		if (ppnode == nullptr)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}

			cur->_parent = ppnode;
		}
	}


	bool IsBalance()
	{
		return _IsBalance(_root);
	}


	int Height()
	{
		return _Height(_root);
	}

	//中序遍历
	void Inorder()
	{
		_Inorder(_root);
	}


private:

	// 根节点->当前节点这条路径的黑色节点的数量
	bool CheckColour(Node* root, int blacknum, int benchmark)
	{
		if (root == nullptr)
		{
			if (blacknum != benchmark)
				return false;

			return true;
		}

		if (root->_col == BLACK)//统计黑色用于判断每条路径黑色都相同
		{
			++blacknum;
		}

		if (root->_col == RED && root->_parent && root->_parent->_col == RED)
		{
			//当前节点与父节点连续红色
			cout << root->_kv.first << "出现连续红色节点" << endl;
			return false;
		}

		return CheckColour(root->_left, blacknum, benchmark)
			&& CheckColour(root->_right, blacknum, benchmark);//递归遍历每条路径
	}

	bool _IsBalance(Node* root)
	{
		//根据构建红黑树的规则进行判断
		if (root == nullptr)
			return true;

		if (root->_col != BLACK)//根不能为红
		{
			return false;
		}

		// //参考值,统计一条路径的黑色节点数
		int benchmark = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				++benchmark;

			cur = cur->_left;
		}

		//通过检查每条路径的黑色节点数判断是否平衡
		return CheckColour(root, 0, benchmark);
	}


	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);

		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	//中序遍历子函数
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << " ";
		_Inorder(root->_right);
	}

private:
	Node* _root = nullptr;

public:
	int _rotateCount = 0;
};

                         感谢你耐心的看到这里ღ( ´･ᴗ･` )比心，如有哪里有错误请踢一脚作者o(╥﹏╥)o！ 

                                       

                                                                         给个三连再走嘛~  

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1291183.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

编织魔法世界——计算机科学的奇幻之旅

编织魔法世界——计算机科学的奇幻之旅

文章目录 每日一句正能量前言为什么当初选择计算机行业计算机对自己人生道路的影响后记 每日一句正能量 人生就像赛跑&#xff0c;不在乎你是否第一个到达尽头&#xff0c;而在乎你有没有跑完全程。 前言 计算机是一个神奇的领域&#xff0c;它可以让人们创造出炫酷的虚拟世界…
阅读更多...
上位机与PLC：ModbusTCP通讯之数据类型转换

上位机与PLC：ModbusTCP通讯之数据类型转换

前请提要： 从PLC读取的数值，不管是读正负整数还是正负浮点数，读取过来后都会变成UInt16，也就是Ushort类型 一、ushort（UInt16）转成 Int32 源代码方法： //ushort类型转Int32类型的方法private int ushortToInt32(ushort[] date, int start){//先进行判断，长度是否正确…
阅读更多...
在线工具分享SQL转ElasticSearchDSL语句

在线工具分享SQL转ElasticSearchDSL语句

&#x1f60a; 作者&#xff1a; 瓶盖子io &#x1f496; 主页&#xff1a; 瓶盖子io-CSDN博客
阅读更多...
vuepress-----10、vssue使用

vuepress-----10、vssue使用

vssue使用 https://vssue.js.org/ 按照文档 https://vssue.js.org/zh/guide/github.html (opens new window) 操作 # 1、创建 OAuth application https://github.com/settings/applications/new (opens new window) # 2、安装插件 yarn add vssue/vuepress-plugin-vssue# 这…
阅读更多...
系统调用过程

系统调用过程

应用程序通过系统调用请求操作系统的服务。而系统中的各种共享资源都由操作系统内核统一掌管&#xff0c;因此凡是与共享资源有关的操作&#xff08;如存储分配、/O操作、文件管理等&#xff09;&#xff0c;都必须通过系统调用的方式向操作系统内核提出服务请求&#xff0c;由…
阅读更多...
基于javaweb实现的学籍管理系统

基于javaweb实现的学籍管理系统

一、 系统架构 前端&#xff1a;jsp | jquery | css 后端&#xff1a;servlet | jstl | sqljdbc 环境&#xff1a;jdk1.6 | mysql 二、代码及数据库 三、功能介绍 01. 登录页 02. 首页 03. 修改个人密码 04. 专业信息管理 05. 班级信息管理 06. 课程信息管理 07. 学籍…
阅读更多...
BigDecimal：高精度计算的秘密武器！

BigDecimal：高精度计算的秘密武器！

大家好&#xff0c;我是小米&#xff01;最近在面试的时候&#xff0c;发现很多公司都喜欢考察关于BigDecimal的问题&#xff0c;所以我决定在这里和大家分享一下我的经验。如果你在面试中曾经遇到过这个问题&#xff0c;或者想要更深入地了解BigDecimal&#xff0c;那就赶紧跟…
阅读更多...
基于vue开发-创建登录页

基于vue开发-创建登录页

我们使用vue创建完成项目后就开始我们的项目页面开发&#xff0c;如有不清楚怎么操作的可以看博主的前一篇文档 使用vue UI安装路由插件-CSDN博客 在src/views文件夹中创建一个登录页面 在此之前&#xff0c;我们可以先安装一个插件、element、vant、iview等等&#xff0c;可…
阅读更多...
数据结构初阶之二叉树的详细解析

数据结构初阶之二叉树的详细解析

个人主页&#xff1a;点我进入主页 专栏分类&#xff1a;C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 数据结构初阶 Linux 欢迎大家点赞&#xff0c;评论&#xff0c;收藏。 一起努力,共赴大厂。 目录 1.前言 2.二叉树各个…
阅读更多...
智能优化算法应用：基于猎食者算法无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用：基于猎食者算法无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用&#xff1a;基于猎食者算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用&#xff1a;基于猎食者算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.猎食者算法4.实验参数设定5.算法结果6.参考文献7.…
阅读更多...
C# WebSocket简单使用

C# WebSocket简单使用

文章目录 前言Fleck调试工具初始化简单使用 前言 最近接到了一个需求&#xff0c;需要网页实现上位机的功能。那就对数据传输的实时性要求很高。那就只能用WebSocket了。这里简单说一下我的WebSocket如何搭建 Fleck C# WebSocket(Fleck) 客户端:html Winfrom Fleck Github官网…
阅读更多...
lorenz相图

lorenz相图

观察Lorenz在各个不同维度上的相图。 lorenz_demo(50) function xdot g(t,x) xdot zeros(3,1); sig 10.0; rho 28.0; bet 8.0/3.0; xdot(1) sig*(x(2)-x(1)); xdot(2) rho*x(1)-x(2)-x(1)*x(3); xdot(3) x(1)*x(2)-bet*x(3); endfunction lorenz_demo(time) [t,x] ode…
阅读更多...
软考高项第四版五组十域表+ITTO背诵笔记及助记

软考高项第四版五组十域表+ITTO背诵笔记及助记

基于第四版做的笔记&#xff0c;助记是自己编的 还是得靠理解记忆&#xff0c;下面是文档&#xff0c;也用anki制作了记忆卡片&#xff0c;需要的可以自行导入卡包
阅读更多...
谷歌推出功能最强大的大语言模型Gemini；大规模语言模型：从理论到实践

谷歌推出功能最强大的大语言模型Gemini；大规模语言模型：从理论到实践

&#x1f989; AI新闻 &#x1f680; 谷歌推出功能最强大的大语言模型Gemini 摘要&#xff1a;谷歌正式推出其迄今为止功能最强大、最通用的大语言模型Gemini。Gemini在许多测试中表现出了最先进的性能&#xff0c;在大部分基准测试中击败了OpenAI的GPT-4。谷歌发布了三种不同…
阅读更多...
直播录屏软件哪个好？这3款软件请你收好

直播录屏软件哪个好？这3款软件请你收好

随着直播文化的兴起&#xff0c;越来越多的人开始尝试通过直播平台分享自己的经验、技能和生活。在这个过程中&#xff0c;选择一款优秀的直播录屏软件变得至关重要&#xff0c;可是直播录屏软件哪个好呢&#xff1f;本文将深入介绍3款备受欢迎的直播录屏软件。通过详细的步骤指…
阅读更多...
SQL语言重温

SQL语言重温

数据库语言重温 笔记背景SQL教程一些最重要的 SQL 命令SQL WHERE 子句SQL AND & OR 运算符SQL ORDER BY 关键字 笔记背景 由于工作需要&#xff0c;现重温简单SQL语言&#xff0c;笔记记录如下。 SQL教程 SQL&#xff08;Structured Query Language:结构化查询语言&…
阅读更多...
[Realtek sdk-3.4.14b] RTL8197FH-VG+RTL8812FR WiFi黑名单及剔除已连接终端功能实现

[Realtek sdk-3.4.14b] RTL8197FH-VG+RTL8812FR WiFi黑名单及剔除已连接终端功能实现

sdk说明 ** Gateway/AP firmware v3.4.14b – Aug 26, 2019**  Wireless LAN driver changes as:  Refine WiFi Stability and Performance  Add 8812F MU-MIMO  Add 97G/8812F multiple mac-clone  Add 97G 2T3R antenna diversity  Fix 97G/8812F/8814B MP issu…
阅读更多...
数字文化大观：TikTok影响下的全球文娱

数字文化大观：TikTok影响下的全球文娱

在数字时代的大潮中&#xff0c;社交媒体平台正成为全球文娱产业的重要引擎之一。而TikTok&#xff0c;作为一款以短视频为特色的社交应用&#xff0c;正深刻地改变着全球文娱的面貌。 本文将深入研究TikTok对全球文娱的影响&#xff0c;探讨数字文化在这一平台的催化下如何迅…
阅读更多...
销售技巧培训课程内容如何设计才能更好地落地

销售技巧培训课程内容如何设计才能更好地落地

销售技巧培训课程内容如何设计才能更好地落地 在当今竞争激烈的市场环境中&#xff0c;销售人员的角色和作用越来越重要&#xff0c;是公司业绩来源的核心&#xff0c;也是公司能否在激烈竞争的市场中立于不败之地的关键。 因此&#xff0c;对销售人员进行有效的销售技巧培训&a…
阅读更多...
redis中使用事务

redis中使用事务

事务是指一个执行过程&#xff0c;要么全部执行成功&#xff0c;要么失败什么都不改变。不会存在一部分成功一部分失败的情况&#xff0c;也就是事务的ACID四大特性&#xff08;原子性、一致性、隔离性、持久性&#xff09;。但是redis中的事务并不是严格意义上的事务&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023