目录
一、最小生成树
(一)Prim朴素版
思路
练习题
代码
(二)kruskal算法
练习题
代码
二、二分图
(一)染色法判定二分图
练习题
代码
(二)匈牙利算法
练习题
代码
一、最小生成树
(一)Prim朴素版
时间复杂度:O()
思路
① 初始化邻接矩阵和dist数组为
② 进行n次循环,将n个点加入S集合
③ 找出不在集合中的离集合最近的点
④ 将点加入S集合,并用s集合更新剩下的点到集合的距离
区别
Prim算法与Dijkstra算法的代码有些相似,不同的是
① st数组表示的是点已经在生成树中,而Dijkstra算法st数组表示的是点是否已经确定了最短路径
② 第一个点到集合的权值为0,所以i为0时不用加上权值
③ 更新时是更新到集合(最小生成树)的最短边,所以min中不用加上dist[t]
④ dist数组在Prim算法中表示的是一个点到最小生成树集合中所有点的最短距离,而在Dijkstra算法中表示的是点到源点的最短距离
练习题
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。数据范围
1≤n≤500,
1≤m≤,
图中涉及边的边权的绝对值均不超过 10000。输入样例:
4 5 1 2 1 1 3 2 1 4 3 2 3 2 3 4 4输出样例:
6
代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
int g[N][N], dist[N]; //稠密图用邻接矩阵存储
bool st[N];
int n, m, res;
void prim() {
memset(dist, 0x3f, sizeof dist); //dist初始化为0x3f3f3f3f
for(int i = 0 ; i < n ; i ++ ) {
int t = -1;
// 找出未加入最小生成树并且离生成树最近的点
for(int j = 1 ; j <= n; j ++) {
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
// 代表没有可以达到的边,即不存在最小生成树
if(dist[t] == 0x3f3f3f3f) {
res = 0x3f3f3f3f;
return;
}
//先加入res再去for循环更新,因为可能有负环,那么会把自己变小,而最小生成树是不能包含负环的
res += dist[t];
st[t] = true;
// 用t去更新其他的边到最小生成树集合的距离
for(int j = 1 ; j <= n ; j ++) {
dist[j] = min(dist[j], g[t][j]);
}
}
}
int main() {
cin >> n >> m;
int u, v, w;
memset(g, 0x3f, sizeof g);
while(m --) {
scanf("%d%d%d",&u,&v,&w);
g[u][v] = g[v][u] = min(g[u][v], w); //无向图存储两条边,有重边存储最短边
}
prim();
if(res == 0x3f3f3f3f) puts("impossible");
else cout << res << endl;
return 0;
}
(二)kruskal算法
主要用于稀疏图,时间复杂度为O(mlogn)
思想:对边权进行排序后,按顺序从小到大,遇到一条边的两个结点不在同一个连通块中(借助并查集)的话,就加入结果并连接起来
步骤
① 对并查集数组p和边结构体初始化
② 对边结构体进行排序
③ 从小到大选取边,不在同一个连通块的话则连接起来并加入res,并计算加入了的边的条数
④ 判断是否有n条边,有的话则整个图是连通的
练习题
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。数据范围
1≤n≤500,
1≤m≤,
图中涉及边的边权的绝对值均不超过 10000。输入样例:
4 5 1 2 1 1 3 2 1 4 3 2 3 2 3 4 4输出样例:
6
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5+5;
struct Edge{
int a, b, c;
// bool operator< (const Edge &W) const {
// return w < W.w;
// }
}edges[N];
int p[N];
bool cmp(Edge a, Edge b) {
return a.c < b.c;
}
int find(int x) { // 并查集,查找祖先
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main() {
int n, m;
cin >> n >> m;
for(int i = 0 ; i <= n; i ++) p[i] = i; //每个点都是孤立的点
for(int i = 0 ; i < m;i ++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
edges[i] = {a, b, c};
}
sort(edges, edges + m, cmp); //从小到大排序
int res = 0, cnt = 0;
// 遍历边结构体,如果a和b未连接,也就是a和b的边还未加入最小生成树,那么加入并记录
for(int i = 0 ; i < m; i ++) {
int a = find(edges[i].a), b = find(edges[i].b);
if(a != b) {
p[a] = b;
res += edges[i].c;
cnt ++;
}
}
//不足n-1条边代表没有最小生成树
if(cnt < n - 1) puts("impossible");
else cout << res << endl;
return 0;
}二、二分图
(一)染色法判定二分图
深搜进行判断二分图,用1和2进行染色。
二分图不一定是连通图,也可能是非连通图。
练习题
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示点 u 和点 v 之间存在一条边。
输出格式
如果给定图是二分图,则输出
Yes,否则输出No。数据范围
1≤n,m≤
输入样例:
4 4 1 3 1 4 2 3 2 4输出样例:
Yes
代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e5+5; //无向图,需要存储两条边,所以双倍
int h[N], e[N], ne[N], idx; //稀疏图用邻接表
int color[N]; //判断是否已经被染色了,且记录被1还是2染色
int n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int x, int c) {
color[x] = c; //染色
for(int i = h[x]; i != -1; i = ne[i]) { //
int j = e[i];
//如果没填过就递归填一下色,或者如果颜色和要填的颜色相同,代表冲突,不是二分图
if((!color[j] && !dfs(j, 3-c) )|| color[j] == c) {
return false;
}
}
return true;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h); //初始化头节点
int a, b;
while(m--) {
scanf("%d%d",&a, &b);
add(a, b), add(b, a); //无向图
}
bool flag = true;
//二分图不一定是连通图,也可能是非连通图。这也是这个for循环存在的意义
for(int i = 1; i <= n; i ++ ) {
if(!color[i]) {
//不连通,所以每个连通块都从1开始就好
if(!dfs(i, 1)) {
flag = false; //有冲突
break;
}
}
}
if(!flag) puts("No");
else puts("Yes");
return 0;
}(二)匈牙利算法
匈牙利算法基础知识可以查阅这篇文章:匈牙利算法详解_Amelie_xiao的博客-CSDN博客_匈牙利算法
- 匈牙利算法(Hungarian algorithm),即图论中寻找最大匹配的算法。
- 匈牙利算法(Hungarian algorithm),主要用于解决一些与二分图匹配有关的问题。
可以比喻成男女匹配的过程

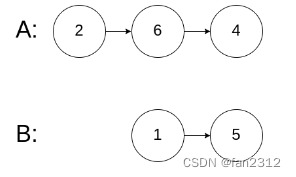
第一个男生和第二个男生都顺利和女生匹配了,此时第三个男生匹配到的是已经心有所属的女生,且这个男生没有别的钟情的女生了,那么为了获得最大匹配数量,我们可以看一下与这女生匹配的一号男生有没有其他可以匹配的女生,发现有,那么将1号男生转换目标,然后三号男生就能顺利牵手了,匹配数也就+1了(绿色线代表取消了)


演示匈牙利算法整个配对的递归过程
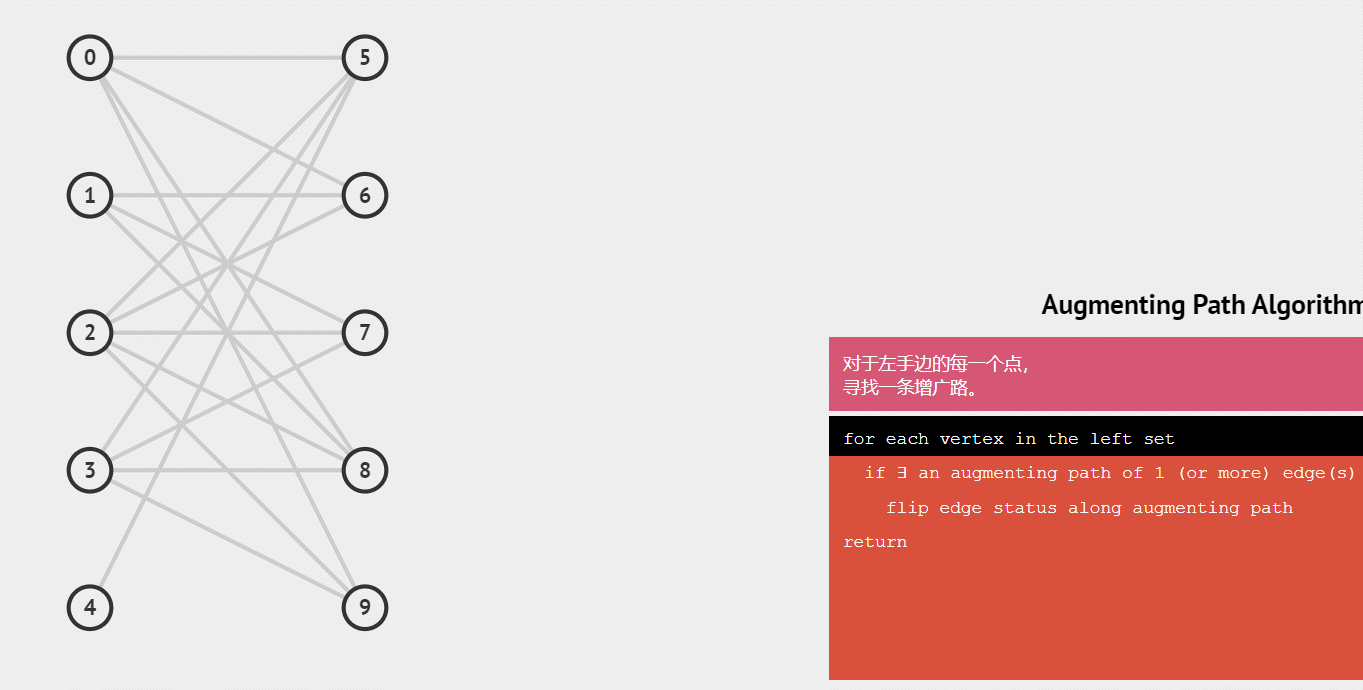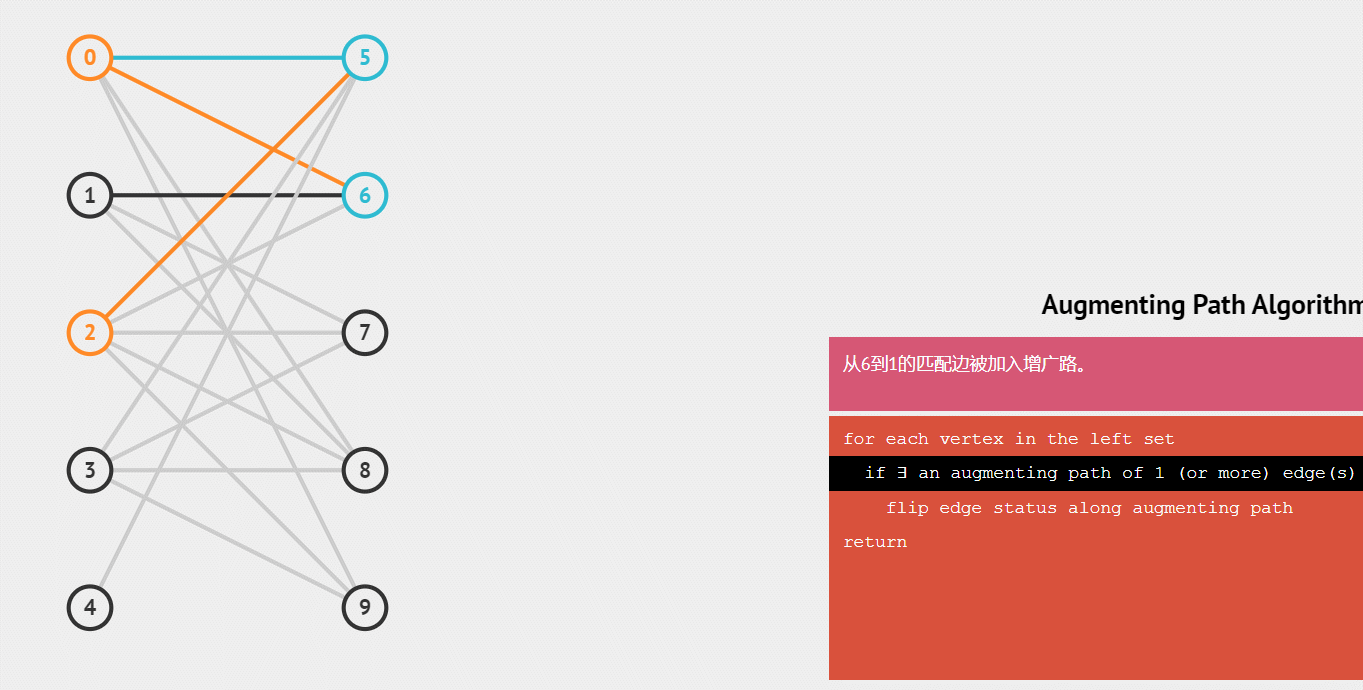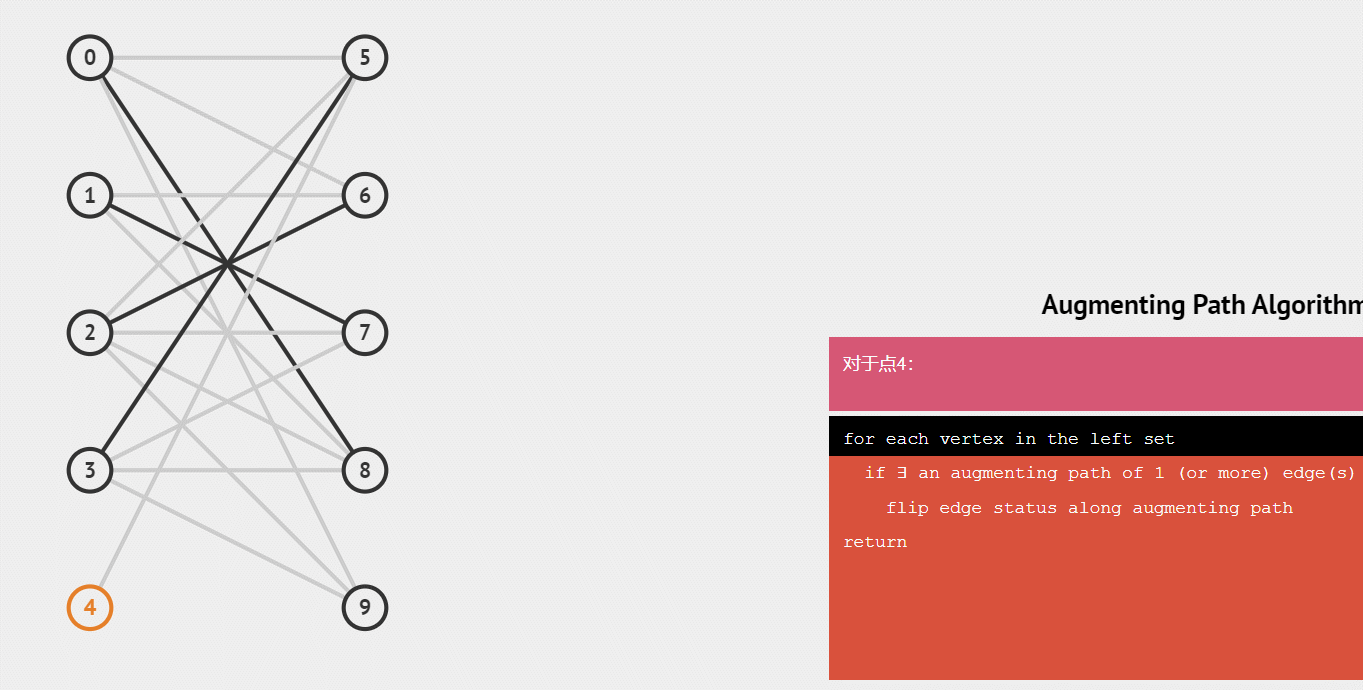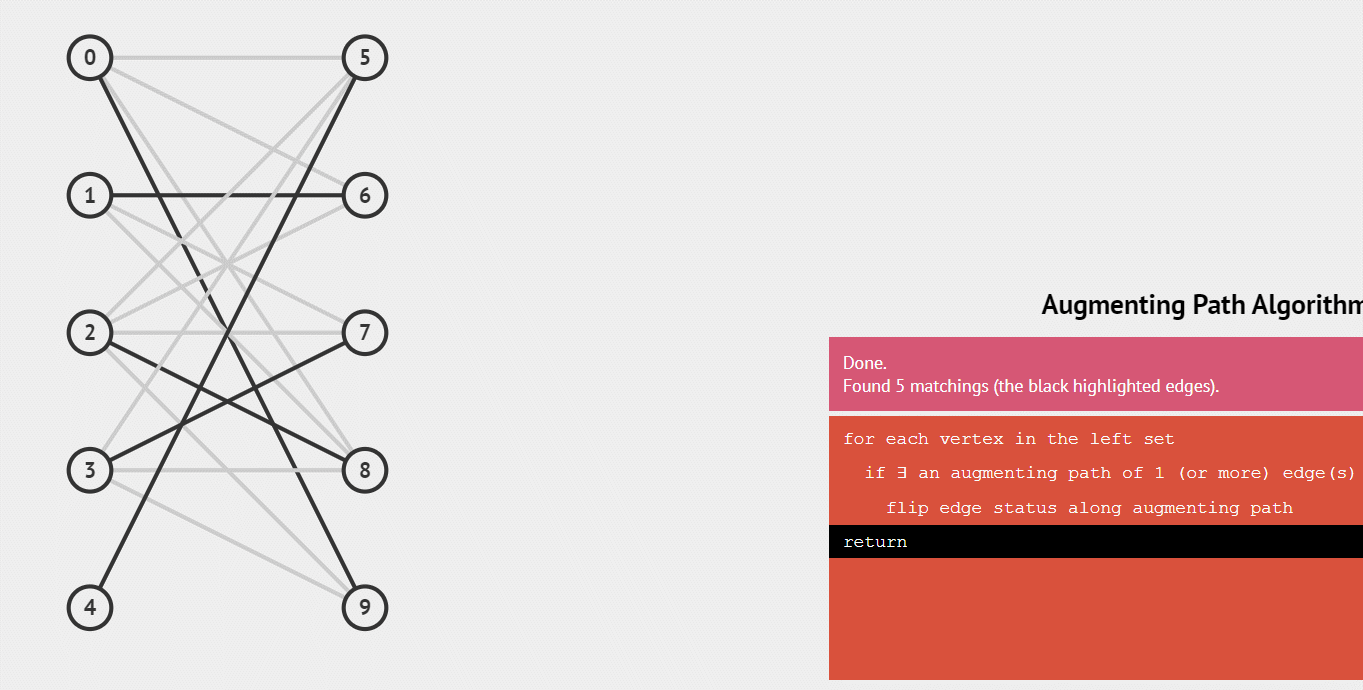
练习题
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤输入样例:
2 2 4 1 1 1 2 2 1 2 2输出样例:
2
代码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 505, M = 2 * 1e5;
int n1, n2, m;
int h[N], e[M], ne[M], idx; //从题意上看是稠密图,可用邻接矩阵或邻接表
int match[N]; //记录女生找的男生是谁,方便下一次的回溯
bool st[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a] , h[a] = idx++;
}
bool find(int x) {
for(int i = h[x]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) //防止重复查询,比如为与她相匹配的男生找下家肯定不能还找那个女生了
{
st[j] = true;
//如果j这个女生没匹配过或者可以将与她相匹配的男生找下家的话,那么就与当前的男生匹配
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
int main() {
cin >> n1 >> n2 >> m;
memset(h, -1, sizeof h);
int a, b;
while(m --) {
scanf("%d%d",&a,&b);
add(a, b) ; //左边部分的点指向右半部分,相当于有向边了
}
int res = 0;
for(int i = 1 ;i <= n1; i ++) { //遍历左边所有的点
memset(st, false, sizeof st); //每次要重置st数组
if(find(i)) res ++;
}
cout << res << endl;
return 0;
}