蓝桥杯寒假集训第二天（分巧克力）

news2024/9/29 19:19:03

没有白走的路，每一步都算数🎈🎈🎈

题目描述：

有很多的巧克力块，需要设计一个程序，让手艺师傅切出来的巧克力既满足切出来的巧克力的份数达到客户要求的份数，并且切出来的巧克力块尽可能的大。

输入描述：

第一行：

输入俩个数据，N，K，N代表原来的大巧克力的块数，K表示客户需要得到的块数

第二行：

接下来每行表示每个巧克力的长度和宽度

输出描述：

输出最终师傅切出来的最大长度

样例输入输出：

样例输入:

2 10

5 6

6 5

样例输出：

暴力解法

1.出现段错误的原因：x的循环没有循环到最后一个，即min(lmin,rmin)+1

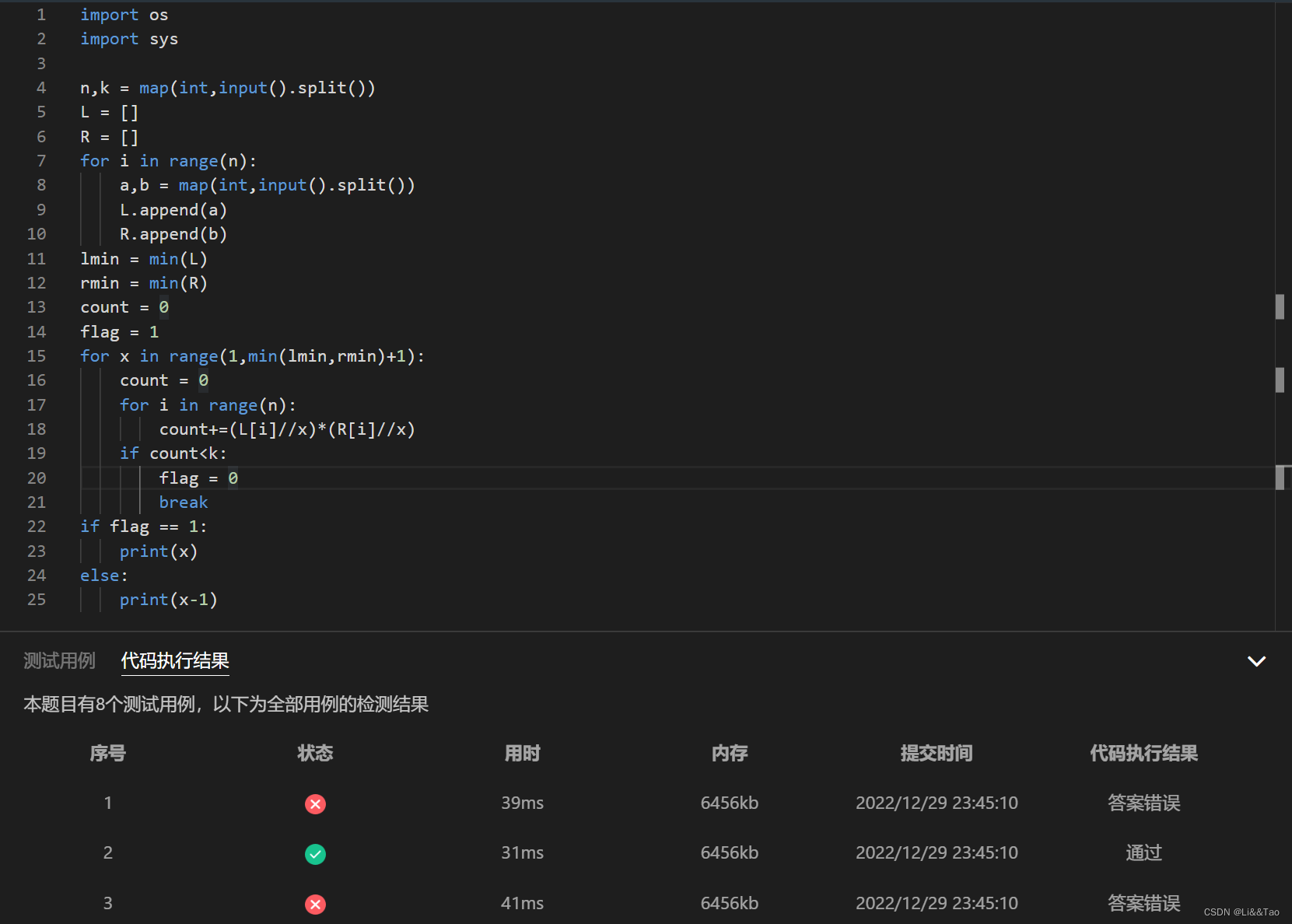
出错原因：

当边长很大的时候，需要的块数相对较小的时候，就有些块是不需要切的，所以这里需要把块的大小给扩大，不应该是min(minl,minr) 。上述的例子，我们输出的不应该是3，还可以是5，6。所以需要设置参数调整一下。

当然这里设置成

lmax = max(L),rmax = max(R)，

x的取值也从1到其中的最大值之后，

自然而然的时间也会增加了。

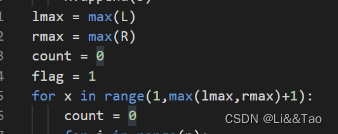
最后就是超时的问题

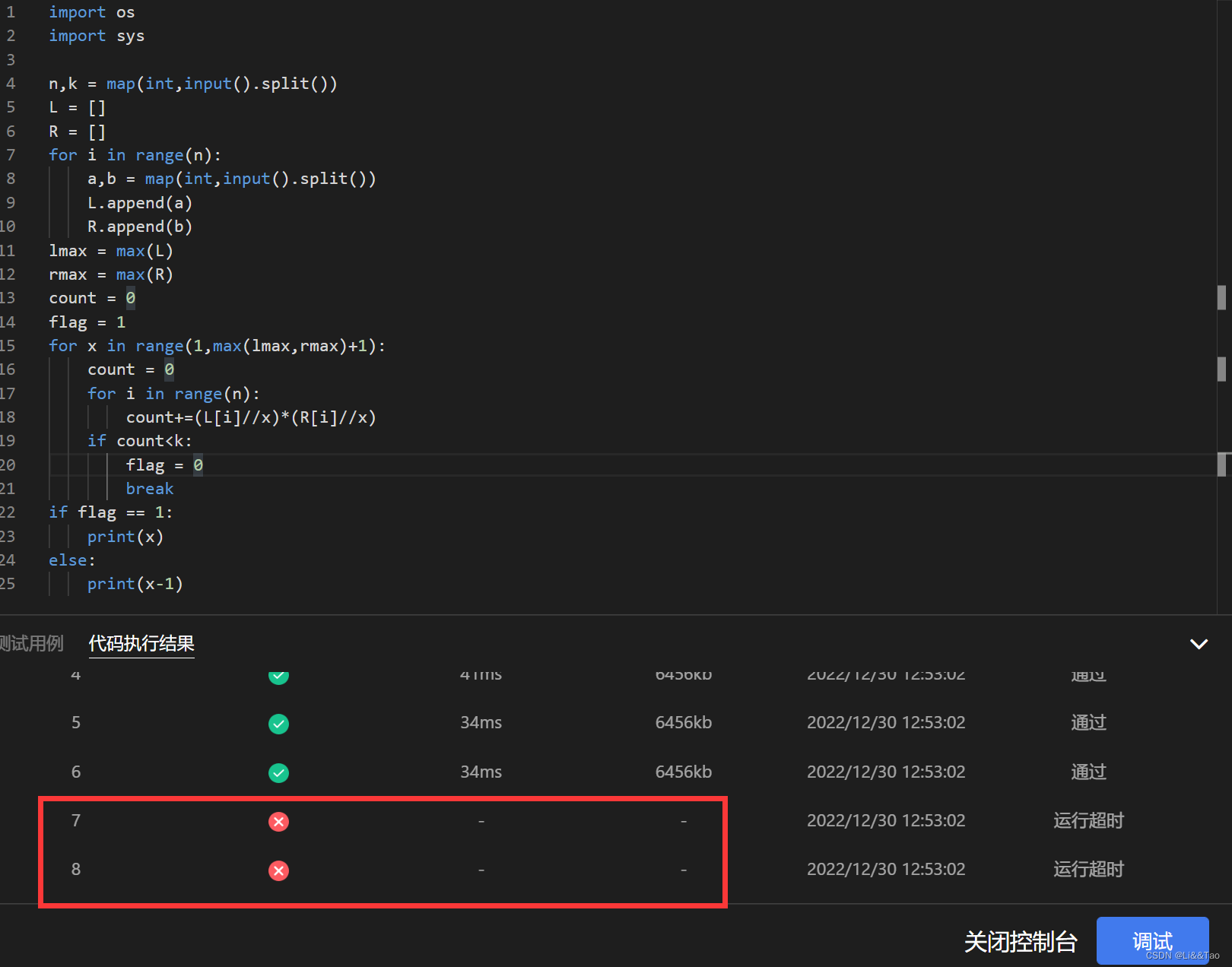
超时的解决办法，采用二分去写

尝试用二分的方法去写

暴力法

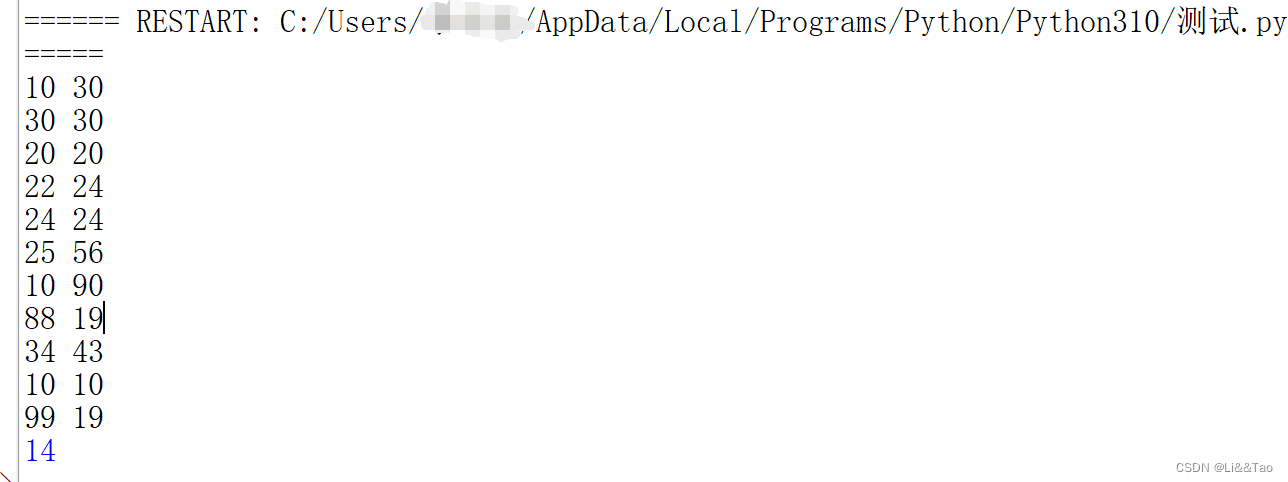
代码：

import os
import sys

n,k = map(int,input().split())
L = []
R = []
for i in range(n):
    a,b = map(int,input().split())
    L.append(a)
    R.append(b)
lmax = max(L)
rmax = max(R)
count = 0
flag = 1
for x in range(1,max(lmax,rmax)+1):
    count = 0
    for i in range(n):
        count+=(L[i]//x)*(R[i]//x)
    if count<k:
        flag = 0
        break
if flag == 1:
    print(x)
else:
    print(x-1)

二分法

第一次尝试，二分法出现了计算结果和正确结果相差为一的情况，这是二分法在数据量较大的时候出现结果比正常的结果多了1

代码：

import os
import sys

n,k = map(int,input().split())
L = []
R = []
for i in range(n):
    a,b = map(int,input().split())
    L.append(a)
    R.append(b)
lmax = max(L)
rmax = max(R)
count = 0
flag = 1
l = 1
r = max(lmax,rmax)
x = 0
##for x in range(1,max(lmax,rmax)+1):
while (r-l)>1:
    x = (l+r)//2
    count = 0
    for i in range(n):
        count+=(L[i]//x)*(R[i]//x)
    if count<k:
        r = x
    elif count>=k:
        l = x
print(x)

细节：

仍然有一些细节没有处理好。

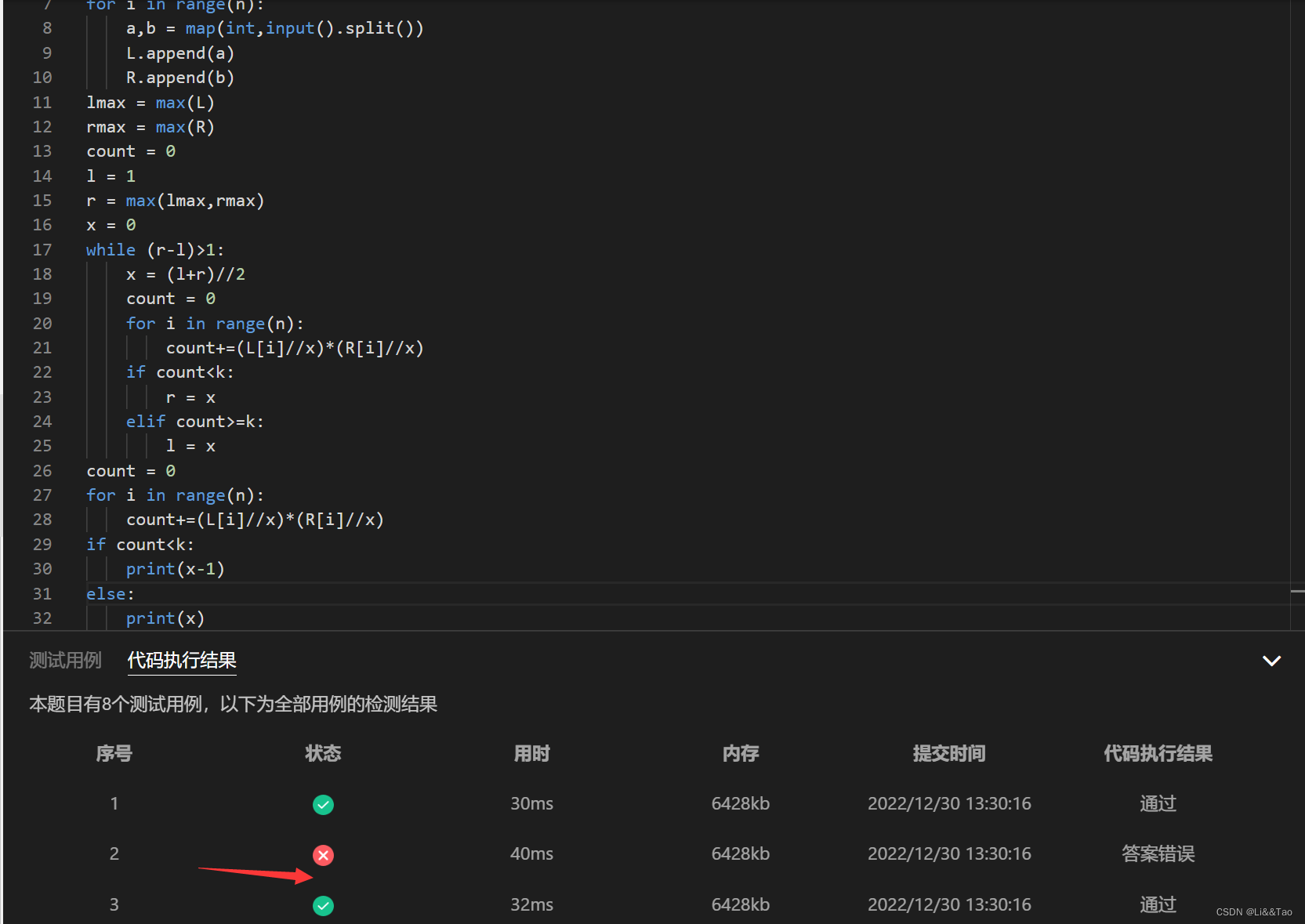
细节处理：

原因是我们最后用二分法求出来的数据会有两个，一个是左边的l,一个是右边的r，需要分成两大类去处理，一种是出先当x=r的时候，这个时候计算出来的coun如果小于k那么就需要输出x-1；第二种情况，当x=l的时候，计算出来可能x+1对应的count仍然大于k。分成这两大类来处理。

最终的AC代码：

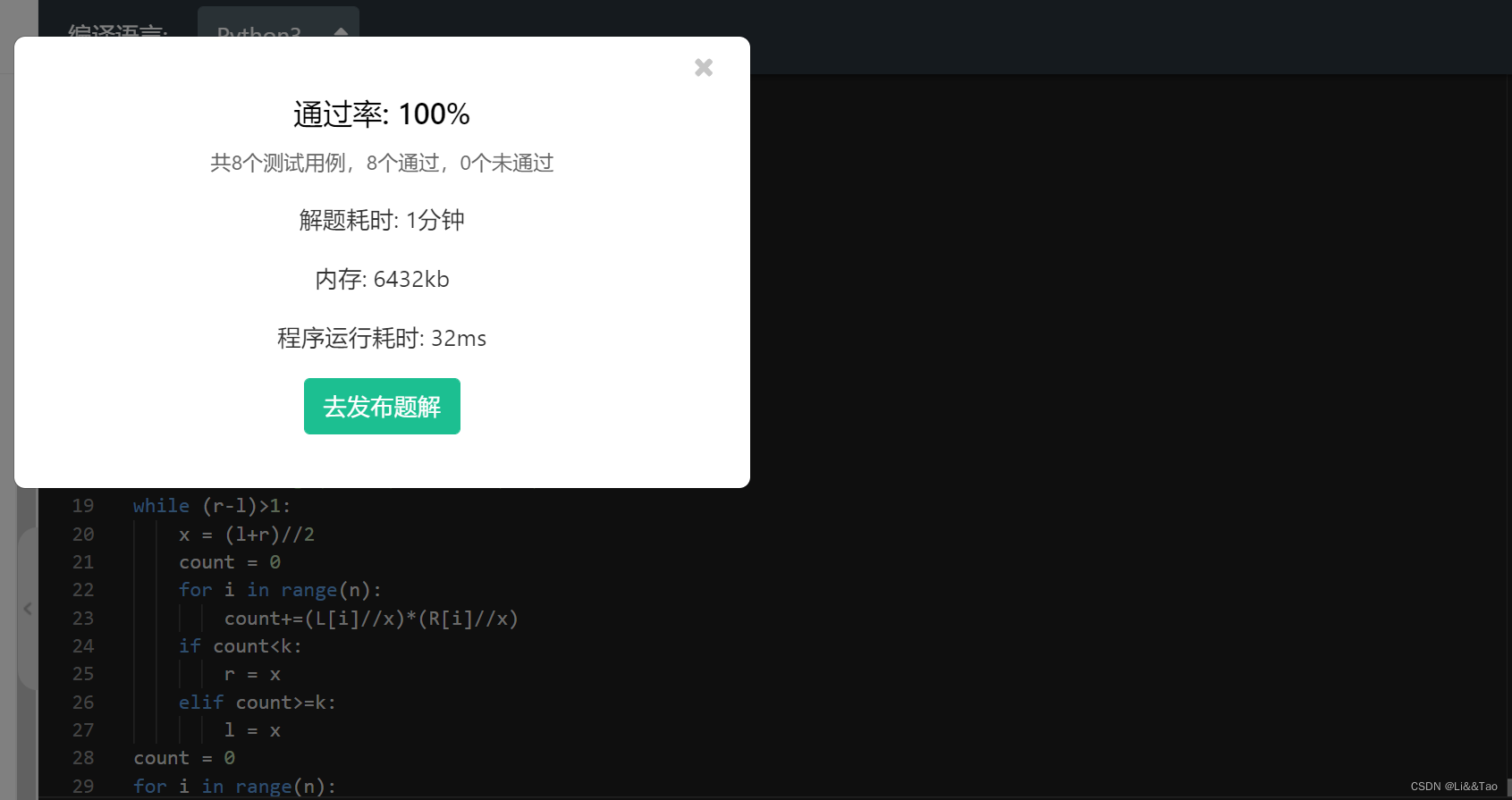
import os
import sys

n,k = map(int,input().split())
L = []
R = []
for i in range(n):
    a,b = map(int,input().split())
    L.append(a)
    R.append(b)
lmax = max(L)
rmax = max(R)
count = 0
l = 1
r = max(lmax,rmax)
x = 0
while (r-l)>1:
    x = (l+r)//2
    count = 0
    for i in range(n):
        count+=(L[i]//x)*(R[i]//x)
    if count<k:
        r = x
    elif count>=k:
        l = x
count = 0
for i in range(n):
    count+=(L[i]//x)*(R[i]//x)
if count<k:
    print(x-1)
else:
    count = 0
    for i in range(n):
        count+=(L[i]//(x+1))*(R[i]//(1+x))
    if count>=k:
        print(x+1)
    else:
        print(x)