“集合划分”这类问题的解题思路

这类题一般都会描述成这个样子：“给你一个数组，是否能将他划分成n个数值相等的子集？”，再或者有些可能题目描述稍微优点隐晦（下面会给出栗子），这类问题实际上是有通法的，通过 “桶 + 回溯 + 剪枝” 的思路便可以迎刃而解；

什么是 “桶 + 回溯 + 剪枝” 呢？

根据题目描述，是让你把数组划分成n个数值相等的子集，即每一个子集的和都是一样的，那么我们就可以求出每一个子集的和是多少（就是把数组每一个值加起来，然后除以要划分的子集个数），那桶是干什么的呢？我们可以用n个桶来装这些子集，每个桶的容量便是子集的和；以下将用一个栗子让你更加清楚~

假设数组nums为[1, 1, 2, 2, 2] ，是否能划分成4个相等子集？

解决过程如下：

先给数组求和，即sum = 8，要将他划分成4个相等的子集，也就是说每个子集的大小因该为sum / 4 = 2，那么便可以创建4个桶，每一个桶的大小为2；

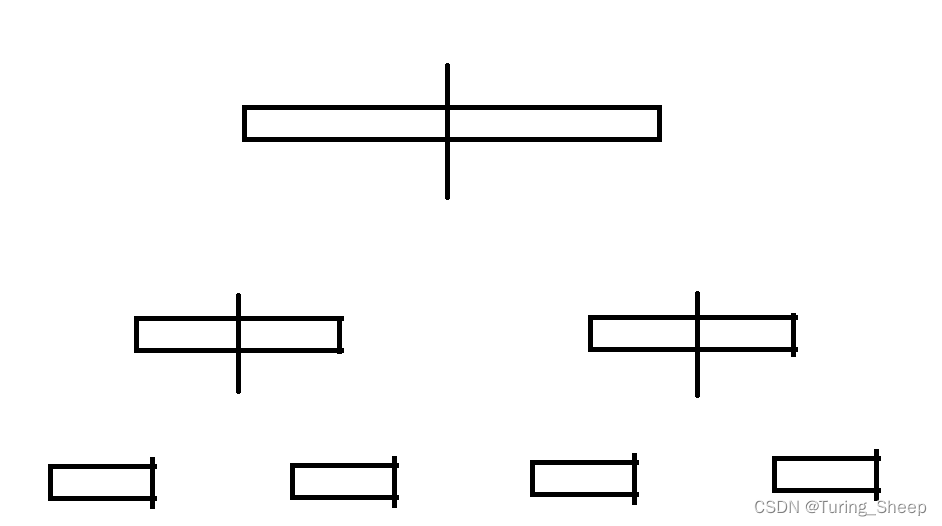
nums[0] = 1，用第一个桶来装，能装下，并且还剩一个位置；nums[1] = 1，继续用第一个桶来装，能正好能把第一个桶装满；nums[2] = 2，用第一个桶来装，发现装不下了，就往第二个桶里装，正好能装满；nums[3] = 2，用第一个桶来装，装不下，在试试用第二个桶来装，装不下，就往第三个桶里装，发现正好能装满；nums[4] = 2，用第一个桶，装不下、用第二个桶，装不下、用第三个桶，装不下、用第四个桶正好能装下；这时候可以发现，四个桶都装满了，那么回原问题上，就相当于可以划分为四个相等的子集；

以上便是一个dfs的全过程，若放错桶，不能将每个桶装满，并且还有剩余数字没有放入桶中，这时便可以回溯回去，再试试其他可能；

如何剪枝呢？

剪枝一：降序排序

不排序也能做对，但是时间上开销就相对较大了，为什么降序排序就可以优化时间呢？我们从num中最大的数开始找，若最大的数都要比子集还要大，或者装下它后，没有装满桶，但是装不下nums中的最小值了，那么这个题的答案一定是false，因为这样一个数的存在，放在哪一个桶里都不合适，通过降序排序，就可以提早发现这个问题，并直接返回false解决；

剪枝二：回溯时若桶的大小等于0，直接返回false

这就表示，如果前面做出选择之后，递归完没有找到任何一个合适的值装满桶，那么回溯撤掉这个值以后，一定为零；比如桶的大小为4，桶中加入了3，但是递归完，发现不存在长度为1的，那么回溯撤掉这个值后桶的大小就是0了；

以上便是这类问题的通解，接下来的两道题，便是“集合划分”的经典问题，思路不能说相似，简直是完全一样；

一、划分为k个相等的子集

题目描述

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例：

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明：有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

题目来源：698. 划分为k个相等的子集 - 力扣（LeetCode）

代码如下：

class Solution {

    public boolean canPartitionKSubsets(int[] nums, int k) {
        if(nums.length < k) {//比均分的数目还小就肯定不能均分
            return false;
        }
        int sum = 0;
        for(int i = 0; i < nums.length; i++) {
            sum += nums[i];
        }
        if(sum % k != 0) {//想要均分成k个区间，那么每个区间的值一定相等，因此sum一定能被k整除
            return false;
        }
        int len = sum / k;//每个区间要满足的大小
        //桶
        int[] bucket = new int[k];
        //剪枝：倒序效率更高
        Arrays.sort(nums);
        for(int i = 0, j = nums.length - 1; i < j; i++, j--) {
            int tmp = nums[i];
            nums[i] = nums[j];
            nums[j] = tmp;
        }
        return dfs(nums, bucket, len, k, 0);
    }

    private boolean dfs(int[] nums, int[] bucket, int len, int k, int index) {
        if(nums.length == index) {
            return true;
        }
        for(int i = 0; i < k; i++) {
            if(bucket[i] + nums[index] > len) {//装不下，就放到下一个桶中去
                continue;
            }
            bucket[i] += nums[index];
            if(dfs(nums, bucket, len, k, index + 1)) {
                return true;
            }
            bucket[i] -= nums[index];
            if(bucket[i] == 0) return false;//到了这儿，若为0，说明没有合适的值等于len
        }
        return false;
    }
}

二、火柴拼正方形

题目描述：

你将得到一个整数数组 matchsticks ，其中 matchsticks[i] 是第 i 个火柴棒的长度。你要用所有的火柴棍拼成一个正方形。你不能折断任何一根火柴棒，但你可以把它们连在一起，而且每根火柴棒必须使用一次。

如果你能使这个正方形，则返回 true ，否则返回 false 。

示例：

输入: matchsticks = [1,1,2,2,2]

输出: true

解释: 能拼成一个边长为2的正方形，每边两根火柴。

代码如下：

class Solution {
    //火柴拼正方形
    public boolean makesquare(int[] matchsticks) {
        int len = matchsticks.length;
        if(len < 4) { //特判:正方形有四条边
            return false;
        }
        //给所有火柴求和
        int sum = 0;
        for(int i = 0; i < matchsticks.length; i++) {
            sum += matchsticks[i];
        }
        if(sum % 4 != 0) { //特判：正方形有四条边
            return false;
        }
        //求出每一条边的长度
        int lenSide = sum / 4;
        //剪枝：降序排序更早触发回溯中的第一个continue
        Arrays.sort(matchsticks);
        //降序
        for(int i = 0, j = matchsticks.length - 1; i < j; i++, j--) {
            int tmp = matchsticks[i];
            matchsticks[i] = matchsticks[j];
            matchsticks[j] = tmp;
        }
        //四个桶
        int[] bucket = new int[4];
        return dfs(matchsticks, lenSide, bucket, 0);
    }

    private boolean dfs(int[] arr, int lenSide, int[] bucket, int index) {
        if(index == arr.length) {
            return true;
        }
        for(int i = 0; i < 4; i++) {
            if(arr[index] + bucket[i] > lenSide) {//桶装不下了
                continue;
            }
            bucket[i] += arr[index];
            if(dfs(arr, lenSide, bucket, index + 1)) {
                return true;
            }
            bucket[i] -= arr[index];
            if(bucket[i] == 0) {
                return false;
            }
        }
        return false;
    }
}