编译器设计(十三)—

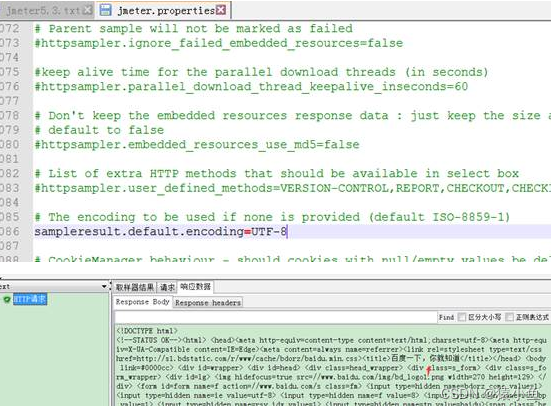
一、简介

对程序块或过程中的操作进行排序以有效利用处理器资源的任务称为指令调度（instruction scheduling）。调度器的输入是由目标机汇编语言操作组成的一个部分有序的列表，输出是同一列表的一个有序版本。

一组指令的执行时间严重依赖于其执行顺序，指令调度会重排一个过程中的各个指令，使每个周期执行尽可能多的指令，以改进其运行时间。处理器常见指令的典型延迟周期：

对于整数加法或减法是1个周期；
对于整数乘法或浮点加减法是3个周期；
对于浮点乘法是5个周期；
对于浮点除法是12-18个周期；
对于整数除法是20-40周期。
load的延迟取决于目标值在内存层次结构中所处的位置，因而该指令的延迟可能是几个周期（比如1-5个，值位于最接近处理器的高速缓存中），也可能是数十到数百个周期（如果值位于内存中）。
算术操作也可以具有可变延迟。例如，如果浮点乘法和除法单元发现实际的操作数使处理过程的某些阶段变得不必要，那么浮点单元将尽早退出处理。

指令调度的主导技术是一种贪婪启发式算法，称为表调度。表调度器运行在无分支代码上，使用各种优先级排序（priority ranking）方案来指引其选择。编译器编写者已经发明了若干框架，用于在代码中大于基本程序块的区域上调度指令。这些区域和循环调度器只是创造条件，使编译器能够将表调度应用到一个更长的操作序列上。

指令调度器的3个主要目标：

第一，它必须保待输入代码的语义。
第二，它应该通过避免拖延或nop指令来最小化执行时间（若不知道这是啥意思，就看流水线冒险）。
第三，它应该尽可能避免延长值的生命周期，至少不能因此导致额外的寄存器溢出。

二、指令调度问题

假定执行下列代码的处理器只有一个功能单元，load和store需要花费3个周期，mult花费两个周期，其他指令均花费一个周期。在这些假定下，原来的代码（下图a）要花费22个周期，调度后的代码（下图b）只需要花费13个周期。
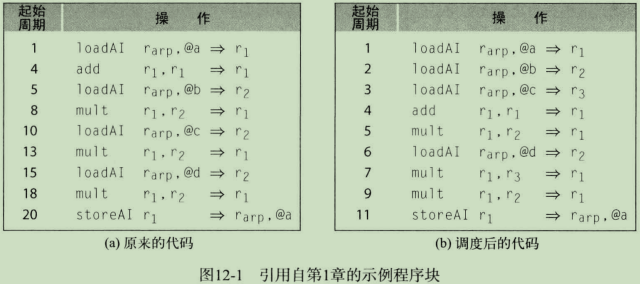
在这里插入图片描述
调度后的代码将长延迟的指令与引用其结果的指令隔离开来，这种分离使得不依赖其结果的指令能够与长延迟指令并发执行。调度后的代码在前三个周期发射load指令，其结果分别在4、5、6周期就绪。这种调度需要一个额外的寄存器r₃来保存第3个并发执行的load指令的结果，但它使得处理器在等待从内存加载第一个算术运算操作数的同时执行一些有用的工作。这种操作之间的重叠执行，实际上隐藏了内存操作的延迟。程序块各处也应用的同一思想隐藏了mult操作的延迟。

这里将会介绍针对单发射的表调度算法，由于市场上的主流处理器都具有多个功能单元，可以在每个周期发射多条指令，所以后面也会介绍如何扩展表调度算法以支持多发射处理器。

指令调度问题定义在基本程序块的依赖关系图 $D$ 之上， $D$ 有时候也称为前趋图， $D$ 的定义是：对于程序块b，其依赖关系图 $D$ = (N，E)，b中的每个操作在 $D$ 中对应于一个结点。对于两个结点n1和n2，如果n2使用了n1的结果，那么 $D$ 中有一条边连接了n1和n2。 $D$ 中的边表示程序块中值的流动，其中的每个结点有两个属性，分别是操作类型和延迟。

$D$ 不是树，它是由多个有向无环图（Directed acyclic graph，DAG）形成的森林，因而，结点可以有多个父结点，而 $D$ 也可以有多个根结点。在 $D$ 中没有前趋结点的那些结点（如下图中的a、c、e和g）称为该图的叶结点，由于叶结点不依赖于任何其他操作，它们可以尽早调度执行。 $D$ 中没有后继结点的结点（如下图中的i）称为该图的根结点，根结点是图中最受限制的结点，因为直至其所有祖先都已经执行之后，它们才能执行。
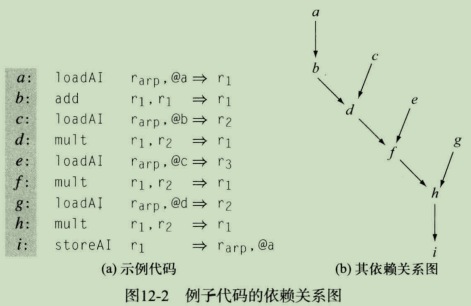
在这里插入图片描述
给出一个代码片断的依赖关系图 $D$ ，调度S将每个结点n（n $\isin$ N）映射到一个非负整数，表示对应操作应该在哪一个周期发射，这里假定第一个操作在周期1发射。这里为指令提供了一个清晰简洁的定义，即第 $i$ 条指令是操作集合 ${n|S(n)=i\}$ 。调度必须满足3个约束：

对于每个n $\isin$ N，都有 $\geqslant 1$ 。这个约束禁止在执行开始之前发射操作，且为一致性起见，调度还必须至少有一个操作 $n^{'}$ 满足 $S (n^{'}) = 1$ 。
如果 $\isin E$ ，那么 $\leqslant S(n2)$ ，其中 $d e l a y (n 1)$ 表示操作 $n 1$ 执行所需要的时间（或叫延迟）。这个约束保证正确性，在一个操作的操作数都已经定义完毕之前，该操作是无法发射的。违反该规则的调度将改变代码中数据的流动，且在静态调度的机器上很可能产生不正确的结果。
每个指令包含的各个类型 $t$ 的操作的数目，不能超过目标机在单个周期的发射能力。这个约束保证了可行性，违反该约束的调度可能会包含一些目标机没有能力发射的指令。（在常见的VLIW机器上，调度器必须用nop填充指令中未使用的槽位。）

编译器只应当产生满足所有3个约束的调度。给出一个良构、正确、可行的调度，该调度的长度只是最后一个操作完成的周期编号，假定第一个指令在周期1发射。调度长度可以如下计算：

$max_{x \in N} (S(n) + delay(n))$

随调度长度的概念而来的是时间最优调度（time-optimal schedule）的概念，如果对包含同一组操作的所有其他调度 $S_j$ ，都有 $L(S_i) \leqslant L(S_j)$ ，那么调度 $S_i$ 是时间最优的。

沿穿越依赖关系图的路径计算总延迟，能够暴露有关该程序块的额外细节。对上文例子中的依赖关系图 $D$ 标注累积延迟的有关信息，将得到下图。从一个结点到计算结束处（根结点）的路径长度被作为结点的上标给出。其值清楚地说明了路径abdfhi是最长的（累计延迟为3+1+2+2+2+3=13），它是决定这个例子总体执行时间的关键路径（依赖关系图中延迟最长的路径）。
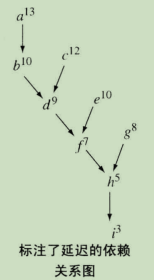
在这里插入图片描述
编译器如何调度这一计算呢？

首先调度 $D$ 中关键路径的叶子结点作为第一条发射指令，这里是a；
a调度后，剩下关键路径是cdfhi ，所以c会作为第二条指令调度；
ac调度后，b和e对应的路径等长且都是关键路径，但b需要a的结果，而这在第四个周期之前不可用，所以这里调度e；
以这种方式继续下去，将产生调度acebdgfhi，这与上图12-1b给出的调度后的代码是匹配的。

反相关：如果操作x位于操作y之前，且y定义了一个x中使用的值，那么称操作x反相关于操作y，记作y $\to$ x。调换其执行次序，将导致x计算出一个不同的值，所以调度器无法将y移到x之前，除非它重命名y的结果。

调度器至少可以用两种方法来生成正确的代码。一种是发现输入代码中存在的反相关并在最终的调度中遵守这种关系，这可以调度生成正确的代码，但是想对于未调度的代码，性能提升并不是很高。

另一种是用重命名值来避免反相关。编译器如果可以系统化的重命名程序块的值，则可以在调度代码之前消除反相关，这样生成的代码性能提升相对较高。但是这中方式存在一个潜在问题，即可能会增加对寄存器的需求，并迫使寄存器分配器逐出更多的值。

最简单的重命名方案在每个值生成时为其分配一个新名字，如对上图12-1a 中的代码重命名将产生下列代码，其依赖关系是没有歧义的，不包含反相关。
在这里插入图片描述

2.1 度量调度质量的其他方式

调度还可以用执行时间之外的其他值度量。同一程序块的两个调度 $S_i$ 和 $S_j$ 对寄存器的需求可能是不同的，即 $S_j$ 中活跃值的最大数目可能小于 $S_i$ 中的最大数目。如果处理器要求调度器为空闲的功能单元插入nop指令，那么 $S_i$ 包含的操作可能少于 $S_j$ ，因而执行时需要取的指令也较少。这不完全依赖于调度长度。例如，在具有可变周期nop指令的处理器上，将多个nop操作串在一起会产生较少的操作，且实际发射的指令数可能也会变少。最后， $S_j$ 在目标系统上的执行能耗可能低于 $S_i$ ，因为它从来不使用某个功能单元，取的指令数目较少，或者在处理器的取指逻辑和译码逻辑之间传输的比特数较少。

2.2 是什么使调度这样难

调度的根本操作是，根据各个操作开始执行的周期，将各个操作分组。对于每个操作，调度器必须选择一个周期。对于每个周期，调度器必须选择一组操作。为平衡这两种视角，调度器必须确保，每个操作只在当其操作数可用时才能发射。

在调度器将操作i放置在周期c中时，这一决策将影响到任何依赖于i结果的操作（在 $D$ 中从i可达的任何操作）的最早置放。如果在周期c中可以合法地执行多个操作，那么调度器的选择可能会改变对许多操作（直接或间接依赖于每个可能置于c中的操作）的最早置放。

【本节总结】：局部指令调度器必须为每个操作指定一个执行周期（这些周期从基本程序块入口开始编号）。在这一过程中，调度器必须确保调度中的任一周期包含的操作都没有超出硬件发射指令的能力。在静态调度处理器上，调度器必须确保每个操作都仅在其操作数就绪后发射，这要求调度器向调度中插入nop指令。在动态调度处理器上，调度器应该使执行导致的预期拖延数量最小化。

三、局部调度表

表调度是一个贪婪启发式方法，而非一个具体的算法，用以调度基本程序块中的各个操作。

3.1 算法

经典表调度将范围限制到无分支代码序列，即运行在一个基本程序块上，使得我们可以忽略一些复杂的调度情况。如，在调度器考虑多个程序块时，一个操作数可能取决于此前在不同程序块中的定义，这在操作数何时就绪的问题上产生了不确定性；而跨越程序块边界的代码移动则产生了另一组复杂情况，可能将操作移动到其此前并不存在的某条路径上，还可以在必要时从某条路径上删除操作。（下一节探讨跨程序块的调度）

为将表调度应用到程序块，调度器遵循一个包含四个步骤的计划。

重命名以避免反相关。为减少调度器受到的约束，编译器需要重命名值，对每个定义都将分配一个唯一的名字。这一步骤不是严格必需的，但它使调度器能够发现原本被反相关掩盖的某些调度，也简化了调度器的实现。
建立依赖关系图 $D$ 。为建立依赖关系图，调度器需要自底向上 遍历程序块。对于每个操作，它都构造一个结点来表示新建的值，调度器会从此结点出发，在该结点与使用其值的每个结点之间添加边，每条边都会被标注上当前操作的延迟。（如果调度器不进行重命名， $D$ 还必须表示反相关。）
为每个操作指定优先级。在每个步骤从可用操作的集合中选择时，调度器使用这些优先级作为指引。表调度器中已经使用过许多优先级方案。调度器可以为每个结点计算几种不同的得分，使用其中之一作为主要排序机制，当有结点得分相同时使用其他记分来打破平局。一种经典的优先级方案是使用从当前结点到乃彴根结点之间、以延迟为权重计算长度时最长路径的长。度其他的优先级方案在12.3.4节描述。
重复选择一个操作并调度它。为调度操作，算法从程序块的第一个周期开始，在每个周期均选择尽可能多的操作发射。接下来，算法将周期计数器加1，更新己就绪可执行的操作的集合，并调度下一个周期。算法将重复这一过程，直至每个操作都已经调度完成。对数据结构精巧的使用使得这一过程十分高效。

重命名和 $D$ 的构建比较简单的，常见的优先级计算会遍历依赖关系图 $D$ 并在其上计算一些量度。算法的核心和理解它的关键在于最后一步——调度算法。下图12-3给出了这一步骤的基本框架，其中假定目标处理器只有一个功能单元。
在这里插入图片描述
调度算法抽象地模拟了被调度程序块的执行，算法会忽略值和操作的细节，而专注于 $D$ 中各条边所规定的时序约束。为跟踪时间，算法在变量Cycle中维护了一个模拟时钟。它将Cycle初始化为1，并在穿越程序块处理时对其加1。

算法使用两个列表来跟踪操作。Ready列表包含了当前周期 可执行的所有操作。如果一个操作位于Ready之中，那么其所有操作数都已经计算完成。最初，Ready包含了 $D$ 中的所有叶结点，因为它们并不依赖于程序块中的其他操作。Active列表包含了在更早的周期中发射但尚未完成的所有操作。每次调度器对Cycle加1时，它会从Active中删除Cycle之前已经完成的任何操作op。算法接下来核对op在 $D$ 中的每个后继结点，以确定相应结点是否能够移入Ready列表中，即是否其所有操作数都已经就绪。