6.17验证二叉树（LC98-M）

news2025/2/27 14:07:46

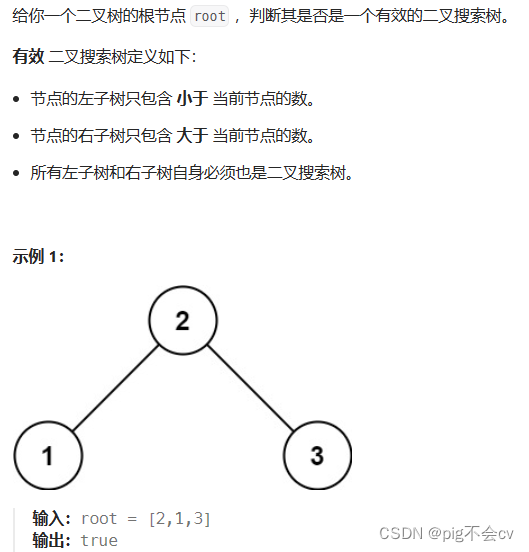
算法：

中序遍历下，输出的二叉搜索树节点的数值是有序序列。

有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。

具体地：中序遍历时，判断当前节点是否大于中序遍历的前一个节点，如果大于，说明满足 BST（Binary Search Tree，二叉搜索树），继续遍历；否则直接返回 false。

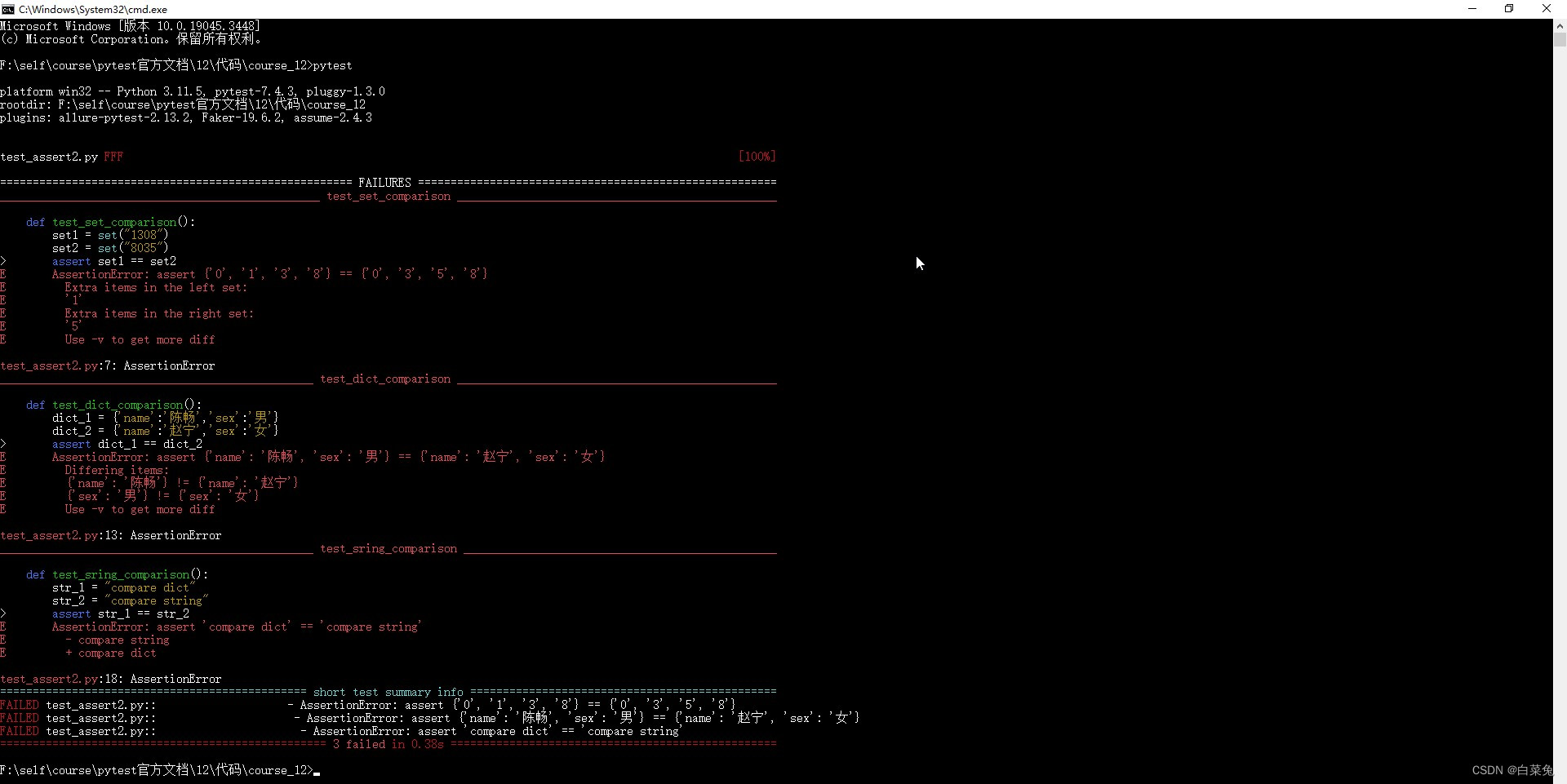
调试过程：

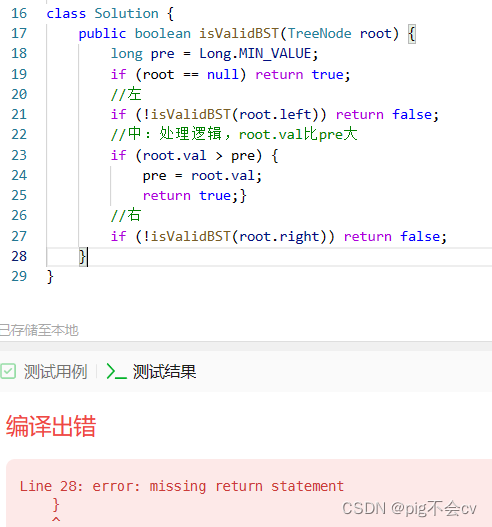
原因：函数没有返回值。

应该把if (!isValidBST(root.right)) return false; 改成 return isValidBST(root.right);

在递归调用中，当返回`true`时，表示当前节点及其子树是一个有效的二叉搜索树。由于二叉搜索树的定义要求左子树的所有节点都小于当前节点，右子树的所有节点都大于当前节点，因此只要发现任何一个子树不满足这个条件，就可以直接返回`false`，不需要再继续执行后面的逻辑。

这两种写法在功能上是等效的，但使用递归时，有时候我们可以更加简洁地表达逻辑。让我们来看看这两种写法的区别和优劣势：

`return isValidBST(root.right);`

这种写法直接返回`isValidBST(root.right)`的结果。如果`isValidBST(root.right)`返回`false`，那么当前的函数也会返回`false`。如果`isValidBST(root.right)`返回`true`，函数会立即中断，并将`true`作为结果返回，表示当前树是一个有效的二叉搜索树。

修改后：

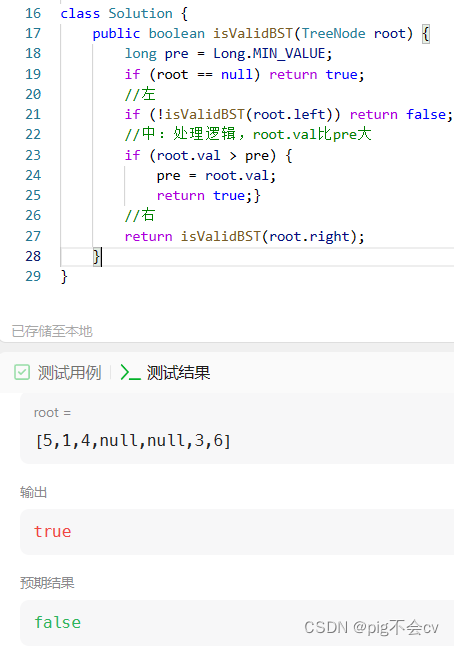
原因：“中”处不应该return true，因为这样直接把这次递归打断了。我们的逻辑是：中序遍历时，判断当前节点是否大于中序遍历的前一个节点，如果大于，说明满足 BST（Binary Search Tree，二叉搜索树），继续遍历；否则直接返回 false。

返回的要是false，只有false能打断这次递归。

修改后：

原因：在递归调用过程中未正确更新`pre`的值。

问题出现在对`pre`的更新上。在代码中，`pre`被声明为局部变量，并且在每次递归调用时都会重新初始化为`root.val`。这意味着每次递归调用时，`pre`都会被重置为当前节点的值，而不会保留之前节点的值。

为了解决这个问题，可以将``pre``声明为实例变量或者将其传递为参数，以便在递归调用中正确地维护前一个节点的值。

正确代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        
        if (root == null) return true;
        //左
        if (!isValidBST(root.left)) return false;
        //中：处理逻辑，root.val比pre大
        if (root.val <= pre) {
            //逻辑不对，直接return false
            return false;
            }
        //若没有return false，则继续遍历
        pre = root.val;         
        //右
        return isValidBST(root.right);
    }
}

注意：

`long pre = Long.MIN_VALUE;`这行代码的作用是初始化一个`long`类型的变量`pre`，并将其赋值为`Long.MIN_VALUE`。

在这里，`Long.MIN_VALUE`是Java中`long`类型的最小值常量。这个值是−2^(63)，即−9223372036854775808。通过将`pre`初始化为`Long.MIN_VALUE`，代码确保了在遍历过程中任何遇到的节点值都会大于这个初始值。这对于比较节点值来判断是否满足BST的性质非常重要。

因此，这行代码的作用是为中序遍历过程中用于比较的先前节点值`pre`进行初始化，以确保它在比较过程中具有一个合适的初始值。

Java中也有`Long.MAX_VALUE`常量，它表示`long`类型的最大值。`Long.MAX_VALUE`的值是2^(63)−1，即9223372036854775807。