线性规划求解-MATLAB Lingo Python实现

线性规划

线性规划是辅助人们进行科学管理的一种数学方法，是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。其展开形式可以表示为如下形式：
$\begin{array}{l} \operatorname{Max}(\operatorname{Min}) \quad z=c_{1} x_{1}+c_{2} x_{2}+\ldots+c_{n} x_{n} \\ \text { s.t. }\left\{\begin{array}{l} a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n} \geq(=\leq) b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n} \geq(=\leq) b_{2} \\ \cdots \cdots \\ a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n} \geq(=\leq) b_{m} \end{array}\right. \\ \end{array}$
在MATLAB中一般用矩阵的形式去表示：
$\begin{array}{l} \min c^{T} x \\ \text { s.t. }\left\{\begin{array}{l} A x \leq b \\ A e q \cdot x=b e q \\ l b \leq x \leq u b \end{array}\right. \end{array}$
从上到下分别代表目标函数、不等式约束条件、等式约束条件、决策变量限制范围。

软件实现

$min \ z = -5x_1 - 4x_2 -6x_3$

$\begin{cases} x_1 - x_2 + x_3 \leq 20 \\ 3x_1 + 2x_2 + 4x_3 \leq 42 \\ 3x_1 + 2x_2 \leq 30 \\ 0 \leq x_1,0 \leq x_2,0 \leq x_3 \end{cases}$

MATLAB

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)线性规划函数。注意MATLAB自带的函数要求不等式都是小于等于，不符合的需要加符号转换。

f = [-5; -4; -6];   % 目标函数系数
A = [1 -1 1
    3 2 4
    3 2 0];
b = [20; 42; 30];
lb = [0;0;0];       % 各变量上下限
ub = [inf; inf; inf];
[x,fval] = linprog(f,A,b,[],[],lb,ub);

x =

0.0000
15.0000
3.0000

fval =

-78.0000

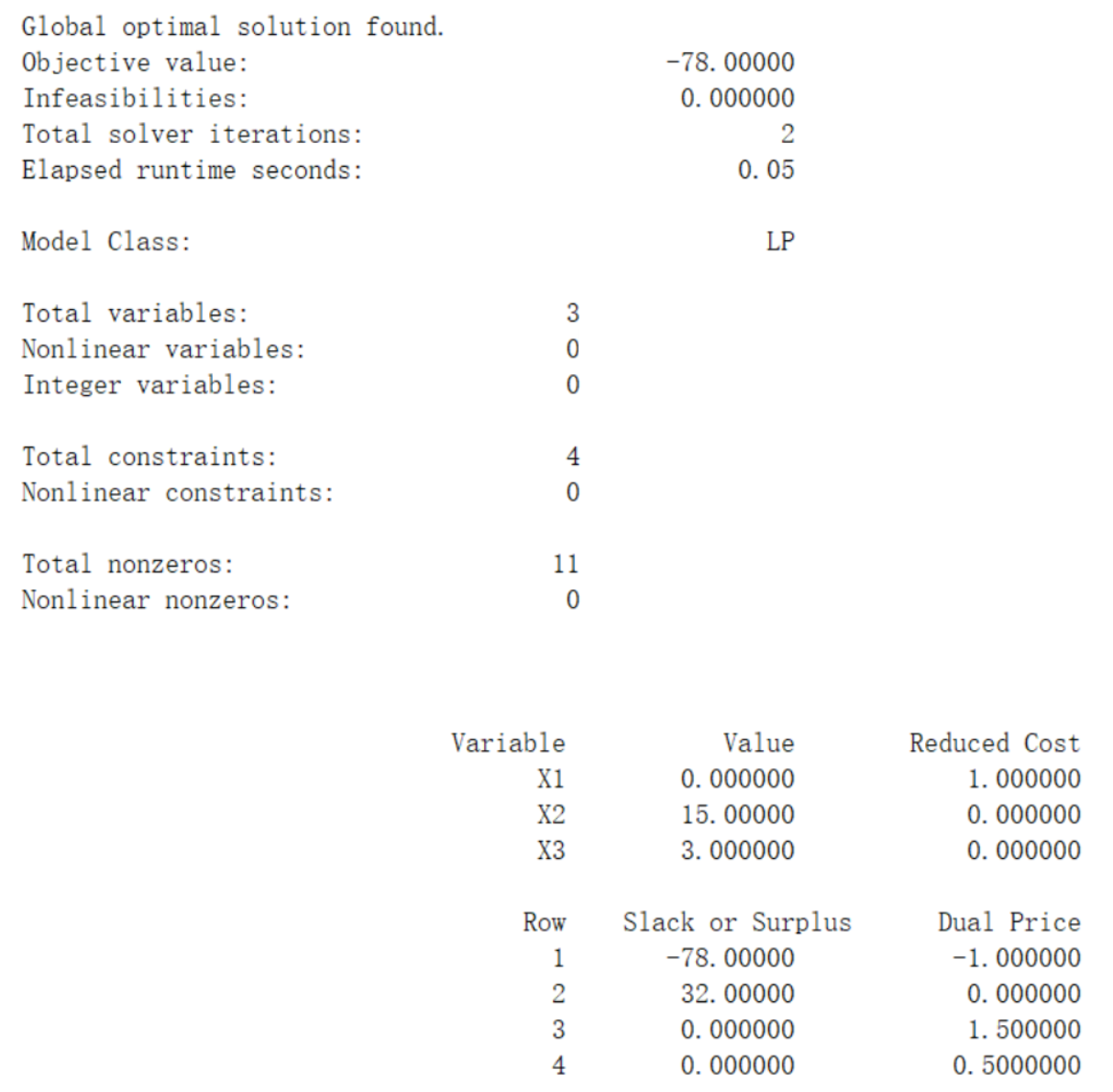
Lingo

min = -5*x1 - 4*x2 - 6*x3;
x1 - x2 + x3 < 20;
3*x1 + 2*x2 + 4*x3 < 42;
3*x1 + 2*x2 < 30;

Python

使用cvxpy工具包

# pip install cvxpy
import cvxpy
x1 = cvxpy.Variable()
x2 = cvxpy.Variable()
x3 = cvxpy.Variable()
f = cvxpy.Minimize(-5*x1-4*x2-6*x3)
c = [
    x1 - x2 + x3 <= 20,
    3*x1 + 2*x2 + 4*x3 <= 42,
    3*x1 + 2*x2 <= 30,
    0 <= x1, 0 <= x2, 0 <= x3
]
prob = cvxpy.Problem(f,c)
mv = prob.solve()
print("min f = %.2f\nx1 = %.2f\tx2 = %.2f\tx3 = %.2f"%(mv, x1.value, x2.value, x3.value))