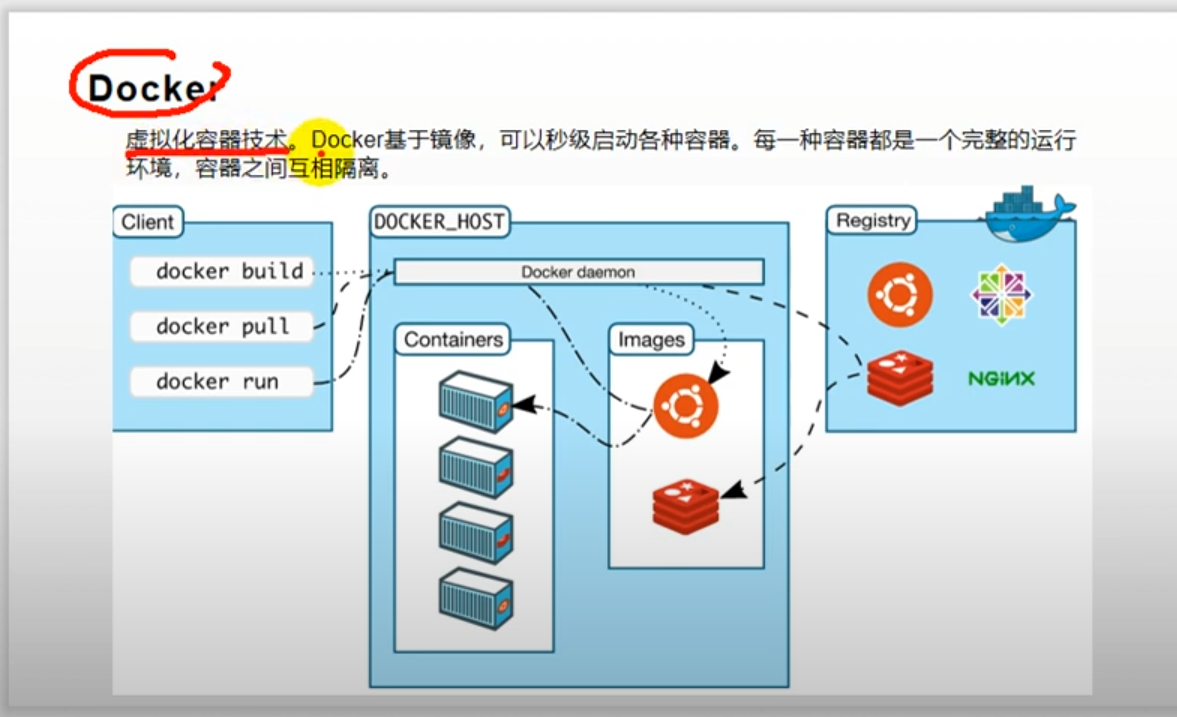
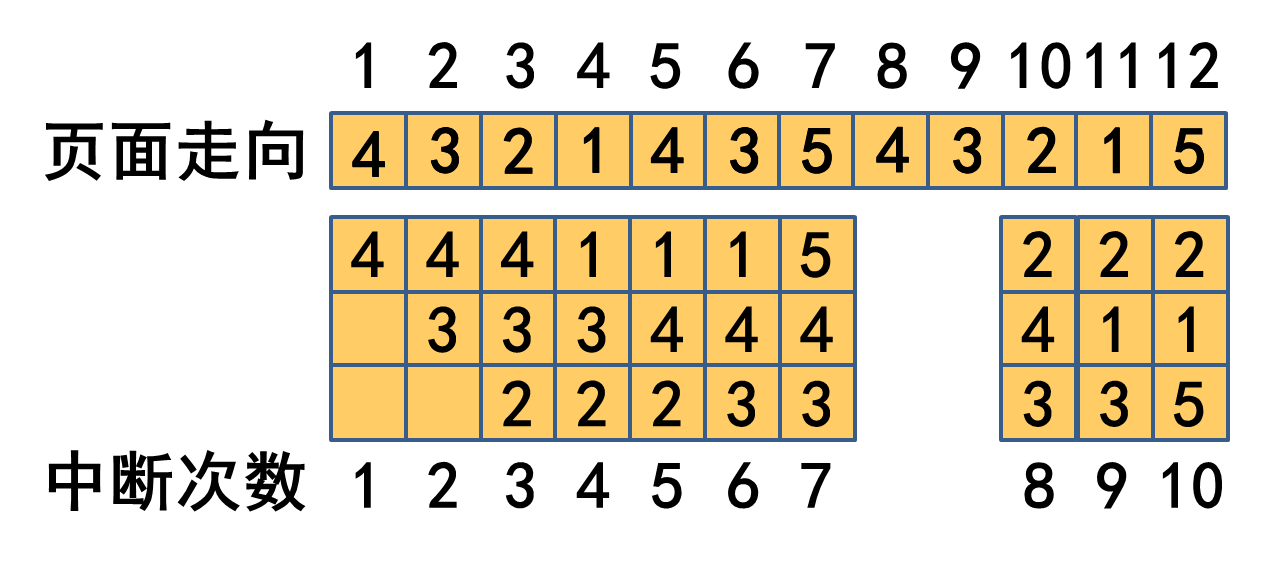
文章目录
- 1 引入
- 2 多目标优化
- 3 更多的定义
- 3.1 支配
- 3.2 非支配集
- 3.3 全局Pareto最优集
- 4 NSGA-II
1 引入
本文主要介绍多目标优化的基本概念以及NSGA-II。
2 多目标优化
多目标优化的优化目标之间存在一定的冲突,例如一个目标增长,导致另一个减少。因此这里的解是一组解决方案而非唯一的全局解。
通常,我们有以下数学问题:
min
/
max
:
f
m
(
x
)
,
m
=
1
,
2
,
…
,
M
s
.
t
.
:
g
j
(
x
)
≥
0
,
j
=
1
,
2
,
…
,
J
h
k
(
x
)
=
0
,
k
=
1
,
2
,
…
,
K
x
i
(
L
)
≤
x
i
≤
x
i
(
U
)
,
i
=
1
,
2
,
…
,
n
\begin{aligned} \min/\max:&f_m(\mathbf{x}),&m&=1,2,\dots,M\\ s.t.:&g_{j}(\mathbf{x})\geq0,&j&=1,2,\dots,J\\ &h_k(\mathbf{x})=0,&k&=1,2,\dots,K\\ &x_i^{(L)}\leq x_i\leq x_i^{(U)},&i&=1,2,\dots,n \end{aligned}
min/max:s.t.:fm(x),gj(x)≥0,hk(x)=0,xi(L)≤xi≤xi(U),mjki=1,2,…,M=1,2,…,J=1,2,…,K=1,2,…,n一个解是包含
n
n
n个变量的向量:
x
=
(
x
1
,
x
2
,
…
,
x
n
)
T
\mathbf{x}=(x_1,x_2,\dots,x_n)^T
x=(x1,x2,…,xn)T此外,问题屈服于
J
J
J个不等式约束和
K
K
K个等式约束,每一个变量都有一个相应的上界和下界。
满足所有约束且在上下界之间的解被称为可行解。所有可行解的集合被称为可行域 (搜索空间) S S S。目标空间由所有可行解对应的的 M M M个目标函数的值构成。
3 更多的定义
3.1 支配
如果条件1和2均满足,则解 x ( 1 ) \mathbf{x}^{(1)} x(1)支配解 x ( 2 ) \mathbf{x}^{(2)} x(2):
- 条件1:对于所有的目标函数均有 x ( 1 ) \mathbf{x}^{(1)} x(1)不差于 x ( 2 ) \mathbf{x}^{(2)} x(2);
- 条件2:在至少一个目标函数上 x ( 1 ) \mathbf{x}^{(1)} x(1)严格优于 x ( 2 ) \mathbf{x}^{(2)} x(2)。
x
(
1
)
\mathbf{x}^{(1)}
x(1)支配
x
(
2
)
\mathbf{x}^{(2)}
x(2)的数学表达为:
x
(
1
)
⪯
x
(
2
)
\mathbf{x}^{(1)}\preceq\mathbf{x}^{(2)}
x(1)⪯x(2)
3.2 非支配集
对于解集 P P P,其非支配集是所有不被其他解所支配的解的集合。
3.3 全局Pareto最优集
S S S的非支配集即为全局Pareto最优集。
一个例子是土木工程中的悬臂梁设计:通过改变悬臂梁长度和直径,来最小化挠度和重量。图1展示了相应的目标空间:不同长度和直径下的挠度与重量变化。

该曲线可以很直观地反应全局Pareto最优集中挠度和重量的权衡。

在图2中靠近原点的目标空间中,形成的一条曲线即为Pareto最优前沿。非可行解也能生成靠近原点的目标值。Pareto前沿表示可能的最佳权衡。
4 NSGA-II
NSGA-II是一种进化算法。进化算法被开发的原因为:直接或基于梯度的技术在处理非线性和复杂交互时存在以下问题:
- 最优解的收敛依赖于初始解的选择;
- 大多数算法易陷入局部最优。
NSGA-II的理解需要一些前驱知识,可以参照:
- 遗传算法简介
- Matlab与遗传算法
- Pymoo与遗传算法
NSGA-II的特征如下:
- 精英准则:种群的精英将更可能传递到下一代;
- 拥挤距离:一种显示的多样性保持机制;
- 着重非支配解。
算法的步骤如下:
- 对父代和后代种群的组合进行非支配排序,并按前沿对它们进行分类,即它们根据非支配级别的升序排序:

- 根据前面的排序来填充新种群;
- 如果一个前沿像F3一样部分采取,则执行拥挤排序,密度较小的是首选;
- 使用拥挤锦标赛选择 (通过前排比较,如果相等则通过拥挤距离比较)、交叉,以及变异算子从这个新种群创建后代种群。




![[Android]视图的控触操作-MotionEvent](https://img-blog.csdnimg.cn/7fd8fd978751449383a4485f8d52d5ba.gif)