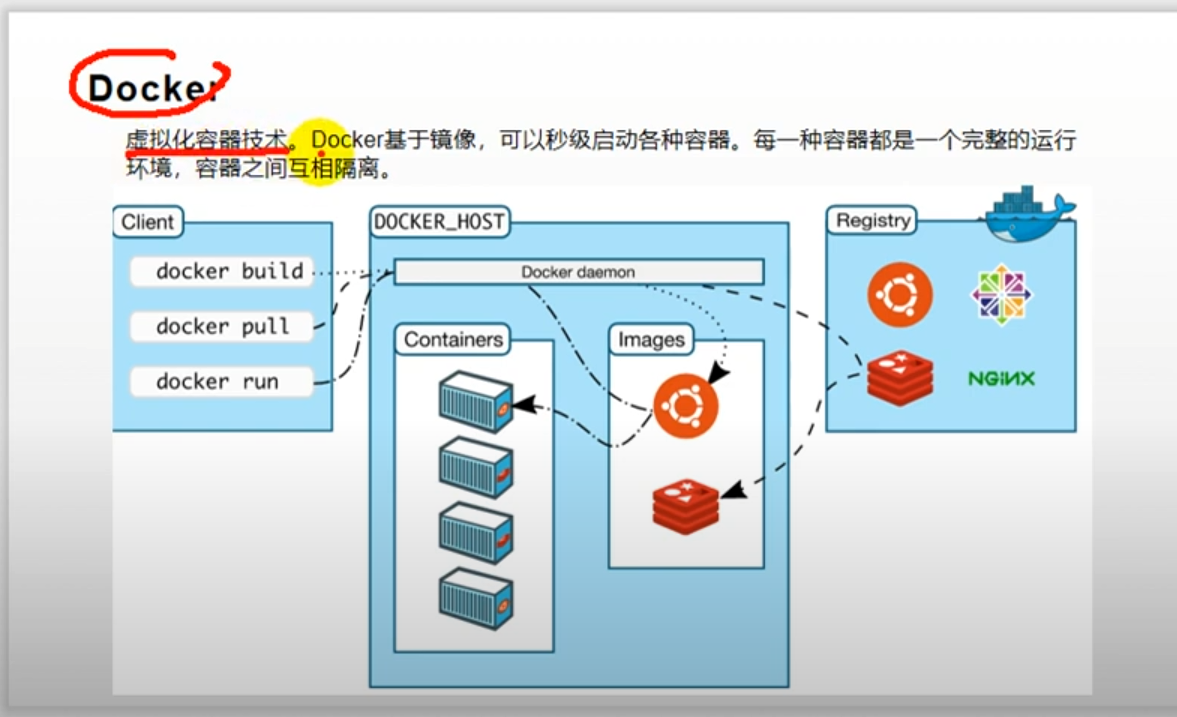
子集和问题(Subset-Sum Problem, SSP)是说给定一个自然数集合 S = { a 1 , a 2 , ⋯ , a n } S=\{a_1,a_2,\cdots,a_n\} S={a1,a2,⋯,an},它含有 n n n个元素,现在又给定一个自然数 s s s,问是否存在 S S S的一个子集 T T T使得 T T T的所有元素之和等于 s s s。
令
t
t
t等于
S
S
S中所有元素之和(
t
=
∑
j
=
1
n
a
j
t=\sum\limits_{j=1}^{n}a_j
t=j=1∑naj)。显然,当
s
>
t
s>t
s>t时,满足要求的子集
T
T
T不存在,直接输出False;当
s
=
t
s=t
s=t时,
T
=
S
T=S
T=S就是满足条件的子集,直接输出True;当
s
=
0
s=0
s=0时,因为空集是
S
S
S的子集且空集的元素之和为
0
0
0,也直接输出True。因此,我们只需要考虑
0
<
s
<
t
0<s<t
0<s<t的情况。
目前有两种流行的解法,一种是搜索(时间复杂度 O ( 2 n ) O\left(2^n\right) O(2n)、空间复杂度 O ( n ) O(n) O(n)),另一种是动态规划(把问题归约为背包问题,时间复杂度 O ( n t ) O(nt) O(nt),空间复杂度 O ( n t ) O(nt) O(nt))。前者的优点是时间复杂度不依赖于 t t t的大小,但是最坏情况下的时间复杂度是指数级的;后者的优点是当 t t t比较小( t < 2 n t<2^n t<2n)时比搜索要快,缺点是当 t ≥ 2 n t\ge 2^n t≥2n时比搜索还慢,而且占用的空间非常大。本文给出了一种能够替代动态规划的策略,使得时间复杂度为 O ( n t ) O(nt) O(nt)的同时空间复杂度只有 O ( n ) O(n) O(n)。当 t t t较大时,我们仍然采用搜索;当 t t t较小时,我们采用这种新的策略。这样,面对 t t t较小的情况时,我们就有了一种高效的且占用空间较少的方法。
我们的新策略的主要思想是利用复数单位根的性质。在我前面的一篇文章里我介绍了如何用单位根巧妙地解决一个数学问题(关于单位根的性质及证明请参见那篇文章),那么在本文中我们将用这个思想给出一个子集和问题的算法。
考虑函数
f
(
x
)
=
∏
j
=
1
n
(
1
+
x
a
j
)
f(x)=\prod\limits_{j=1}^{n}\left(1+x^{a_j}\right)
f(x)=j=1∏n(1+xaj)将它展开为多项式
f
(
x
)
=
c
0
+
c
1
x
+
c
2
x
2
+
⋯
+
c
t
x
t
f(x)=c_0+c_1x+c_2x^2+\cdots+c_tx^t
f(x)=c0+c1x+c2x2+⋯+ctxt其中每项的系数
c
p
c_p
cp等于集合
S
=
{
a
1
,
a
2
,
⋯
,
a
n
}
S=\{a_1,a_2,\cdots,a_n\}
S={a1,a2,⋯,an}的所有和为
p
p
p的子集的个数(
c
p
=
∣
{
T
∣
T
⊆
S
,
s
u
m
(
T
)
=
p
}
∣
c_p=\left|\left\{T|T\subseteq S,\,\mathrm{sum}(T)=p\right\}\right|
cp=∣{T∣T⊆S,sum(T)=p}∣)。那么我们要求解的问题本质上就是判断
c
s
c_s
cs是否等于
0
0
0。将
f
(
x
)
f(x)
f(x)除以
x
s
x^s
xs得
f
(
x
)
x
s
=
c
0
x
−
s
+
c
1
x
1
−
s
+
⋯
+
c
s
+
c
s
+
1
x
+
⋯
+
c
t
x
t
−
s
\frac{f(x)}{x^s}=c_0x^{-s}+c_1x^{1-s}+\cdots+c_s+c_{s+1}x+\cdots+c_t x^{t-s}
xsf(x)=c0x−s+c1x1−s+⋯+cs+cs+1x+⋯+ctxt−s现在我们在复数域上考虑问题。令
z
∈
C
z\in\mathbb{C}
z∈C,代入上式得
z
−
s
f
(
z
)
=
∑
j
=
0
t
c
j
z
j
−
s
z^{-s}f(z)=\sum\limits_{j=0}^{t}c_j z^{j-s}
z−sf(z)=j=0∑tcjzj−s下面考虑利用单位根的性质。设
ω
=
e
2
π
i
m
=
cos
2
π
m
+
i
sin
2
π
m
\omega=e^{\frac{2\pi i}{m}}=\cos\frac{2\pi}{m}+i\sin\frac{2\pi}{m}
ω=em2πi=cosm2π+isinm2π是
m
m
m次单位根,满足
ω
m
=
1
\omega^m=1
ωm=1。我们又知道
∑
k
=
0
m
−
1
(
ω
k
)
u
=
{
0
,
u
不是
m
的倍数
m
,
u
是
m
的倍数
\sum\limits_{k=0}^{m-1}\left(\omega^k\right)^u=\begin{cases} 0,&u\text{不是}m\text{的倍数}\\ m,&u\text{是}m\text{的倍数} \end{cases}
k=0∑m−1(ωk)u={0,m,u不是m的倍数u是m的倍数对于任何整数
u
u
u(不论正负)都成立。这给了我们分离出系数
c
s
c_s
cs的可能。考虑求和
∑
k
=
0
m
−
1
(
ω
k
)
−
s
f
(
ω
k
)
=
∑
j
=
0
t
[
∑
k
=
0
m
−
1
c
j
(
ω
k
)
j
−
s
]
\sum\limits_{k=0}^{m-1}{\left(\omega^k\right)}^{-s}f\left(\omega^k\right)=\sum\limits_{j=0}^{t}\left[\textcolor{orange}{\sum\limits_{k=0}^{m-1}c_j{\left(\omega^k\right)}^{j-s}}\right]
k=0∑m−1(ωk)−sf(ωk)=j=0∑t[k=0∑m−1cj(ωk)j−s]我们希望在
j
−
s
≠
0
j-s\ne 0
j−s=0时方括号里的值为
0
0
0,仅当
j
−
s
=
0
j-s=0
j−s=0即
j
=
s
j=s
j=s时不为
0
0
0,这样上式的值就会变成
m
c
s
mc_s
mcs,我们从而可以求出
c
s
c_s
cs的值。而
j
−
s
j-s
j−s的跨度是从
−
s
-s
−s到
t
−
s
t-s
t−s,我们希望
−
s
>
−
m
-s>-m
−s>−m,
t
−
s
<
m
t-s<m
t−s<m,这样除了
j
=
s
j=s
j=s时以外方括号里的值都一定为
0
0
0。
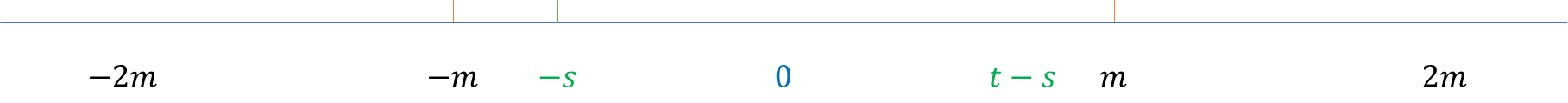
因此有
m
>
s
m>s
m>s且
m
>
t
−
s
m>t-s
m>t−s。为了方便计算,
m
m
m应越小越好,因此取
m
=
max
(
s
,
t
−
s
)
+
1
m=\max(s,t-s)+1
m=max(s,t−s)+1。这样,我们就能计算出
c
s
=
1
m
∑
k
=
0
m
−
1
ω
−
k
s
f
(
ω
k
)
=
1
m
∑
k
=
0
m
−
1
e
−
2
π
i
s
k
m
f
(
e
2
π
i
k
m
)
\begin{aligned} c_s&=\frac{1}{m}\sum\limits_{k=0}^{m-1}\omega^{-ks}f\left(\omega^k\right)\\ &=\textcolor{dodgerblue}{\frac{1}{m}\sum\limits_{k=0}^{m-1}e^{-\frac{2\pi isk}{m}}f\left(e^{\frac{2\pi ik}{m}}\right)} \end{aligned}
cs=m1k=0∑m−1ω−ksf(ωk)=m1k=0∑m−1e−m2πiskf(em2πik)计算
f
(
e
2
π
i
k
m
)
f\left(e^{\frac{2\pi ik}{m}}\right)
f(em2πik)需要
O
(
n
)
O(n)
O(n)的时间,求和需要
O
(
m
)
O(m)
O(m)的时间,所以总共需要花费
O
(
n
m
)
O(nm)
O(nm)的时间。又
m
≤
t
m\le t
m≤t,故最坏情况下需要花费
O
(
n
t
)
O(nt)
O(nt)的时间。计算过程中我们只花了
O
(
1
)
O(1)
O(1)的空间,所以程序花费的总空间是存储
a
1
,
a
2
,
⋯
,
a
n
a_1,a_2,\cdots,a_n
a1,a2,⋯,an所用的
O
(
n
)
O(n)
O(n)的空间。这样,相比于背包问题的动态规划解法,我们节约了大量的空间。
因此,我们的算法是这样设计的:首先特判 s = 0 s=0 s=0, s = t s=t s=t, s > t s>t s>t的情况。接下来求出 m = max ( s , t − s ) + 1 m=\max(s,t-s)+1 m=max(s,t−s)+1的值,若 m > 2 n m>2^n m>2n调用搜索算法求解,若 m ≤ 2 m m\le 2^m m≤2m调用蓝色式子求解。在计算复数的过程中我们反复利用了欧拉公式 e i θ = cos θ + i sin θ e^{i\theta}=\cos\theta+i\sin\theta eiθ=cosθ+isinθ。计算函数 f f f时我的思路是传入 θ = 2 π k m \theta=\frac{2\pi k}{m} θ=m2πk作为参数(而不是直接传入复数 z = e i θ z=e^{i\theta} z=eiθ),而 f ( z ) = ∏ j = 1 n ( 1 + z a j ) f(z)=\prod\limits_{j=1}^{n}\left(1+z^{a_j}\right) f(z)=j=1∏n(1+zaj),所以 z a j = cos a j θ + i sin a j θ z^{a_j}=\cos a_j\theta+i\sin a_j\theta zaj=cosajθ+isinajθ,这样就避免了求复数 z z z的 a j a_j aj次方,从而降低了误差。最终,我们得到 c s c_s cs后,理论上来讲如果和为 s s s的子集不存在那么 c s c_s cs应该为 0 0 0,但是因为计算过程中有舍入误差的存在,所以我们把子集不存在的条件放宽为 ∣ c s ∣ < 1 2 |c_s|<\frac{1}{2} ∣cs∣<21,这样可以很大程度上避免误差带来的问题。同时,当 c s c_s cs计算的比较精确时,它实际上就等于和为 s s s的子集的个数。
完整的Python代码如下:
# encoding: utf-8
import math
from typing import *
class SubsetSumSolver:
def __init__(self, a: List[int], s: int):
self.a = a
self.s = s
self.n = len(a)
self.t = sum(a)
def search(self, u: int, m: int) -> bool: # search method (m>2^n)
if m == 0:
return True
if u == 0:
return False
if m >= self.a[u - 1] and self.search(u - 1, m - self.a[u - 1]):
return True
return self.search(u - 1, m)
def f(self, theta: float) -> complex:
r = 1.
for h in self.a: # h: a_j
arg = h * theta # a_j*θ
r *= 1 + math.cos(arg) + 1j * math.sin(arg) # r*=(1+e^(i*a_j*θ))
return r
def complex_method(self) -> complex:
m = max(self.s, self.t - self.s) + 1
r = 0 # result
for k in range(m):
theta = 2 * math.pi * k / m
f_result = self.f(theta) # f(e^(2πik/m))
theta *= -self.s
zs = math.cos(theta) + 1j * math.sin(theta) # e^(2πisk/m)
r += zs * f_result
r /= m
return r
def solve(self) -> bool:
if self.s > self.t:
return False
if self.s == self.t:
return True
if self.s == 0:
return True
if max(self.s, self.t - self.s) + 1 > 2 ** self.n: # see if m>2^n
return self.search(self.n, self.s)
else:
return abs(self.complex_method()) > 0.5
a = [73383, 66729, 31459, 76611, 70029, 11389, 10089, 63531, \
87311, 64114, 1566, 30601, 45294, 92796, 57129, 18475, 17759, \
25253, 93402]
s = 242514 # test data
solver = SubsetSumSolver(a, s)
print(solver.solve())
这个算法在绝大多数情况下都可以正常运行,除非出现一些特别极端的情况,比如 f ( z ) f(z) f(z)的模长特别大(接近 2 n 2^n 2n),则会放大舍入误差,造成结果不准确。不过经过我的测试,这种情况出现的概率微乎其微(我的测试数据还没有出现过这种情况),所以不必担心。




![[Android]视图的控触操作-MotionEvent](https://img-blog.csdnimg.cn/7fd8fd978751449383a4485f8d52d5ba.gif)