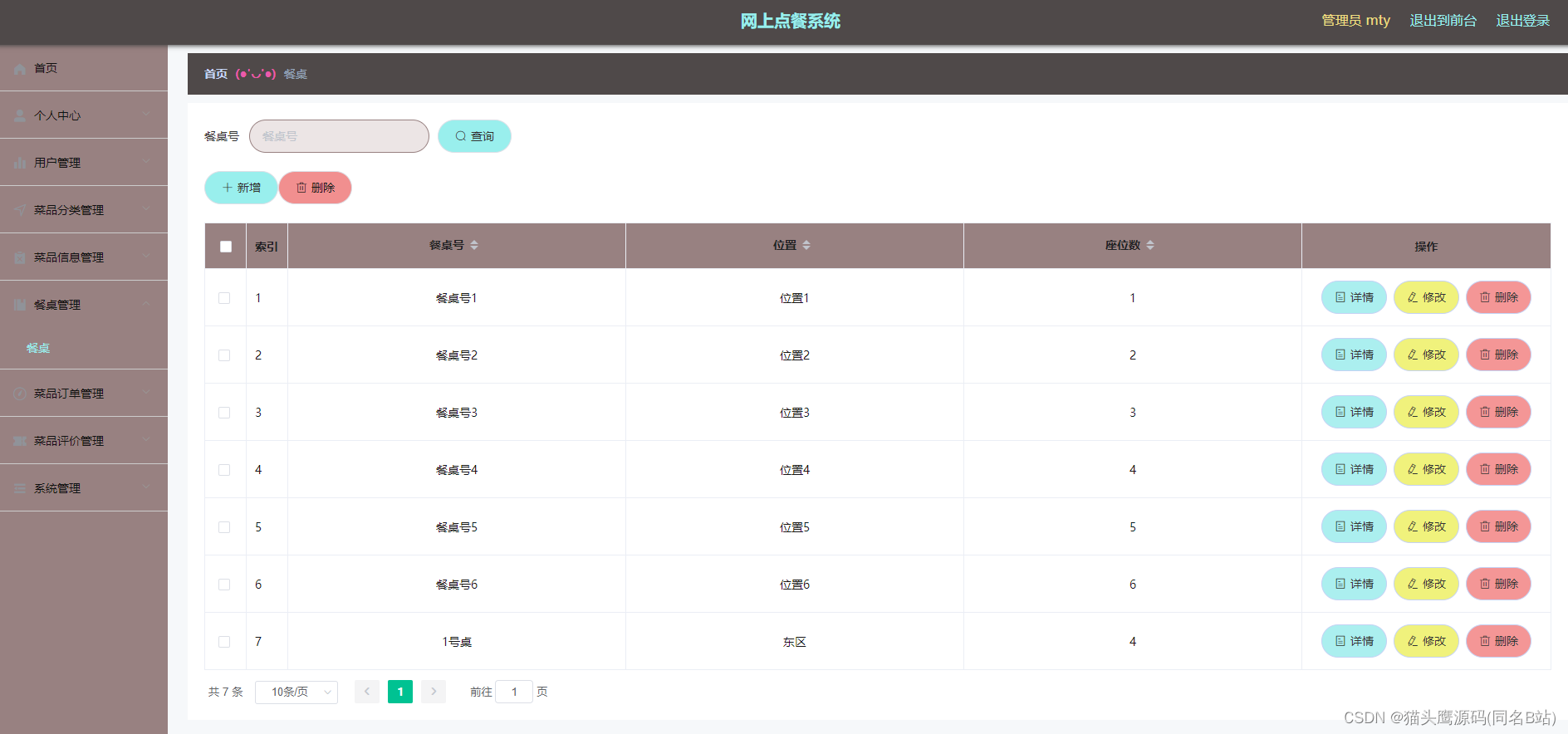
个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
前言:这个专栏主要讲述递归递归、搜索与回溯算法,所以下面题目主要也是这些算法做的
我讲述题目会把讲解部分分为3个部分:
1、题目解析
2、算法原理思路讲解
3、代码实现
一、汉诺塔问题
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目:
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = [] 输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = [] 输出:C = [1, 0]
提示:
- A中盘子的数目不大于14个。
二、解法
题目解析
题目描述说有3根柱子,我们我们分别以A,B,C命名3根柱子。初始应是如下图:
让我们编写程序,让盘子从第一根柱子移到最后一根柱子

算法原理思路讲解
如何去写一个递归
1、先找到相同的子问题 函数头的设计
2、只关心某一个子问题是如何解决的 函数体的书写
3、注意一下递归函数的出口 终止条件
先找到相同的子问题
我们观察下图:
当n=1时,我们只用将A柱子的盘子,移到C柱子即可
当n=2时,我们将A柱子上面的盘子移到B柱子,再将A柱子下面的盘移到C柱子,再将B柱子的盘子移到C柱子
当n=3时,我们将A柱子除了最后一个盘子移到B柱子,再将A柱子下面的最后一盘移到C柱子,再将B柱子的盘子移到C柱子
当n=n时,我们将A柱子(n-1)个盘子移到B柱子,再将A柱子下面的最后一盘移到C柱子,再将B柱子的(n-1)个盘子移到C柱子

函数头的设计
我们设计4个变量
void dfs(vector<int>& x, vector<int>& y, vector<int>& z,int n)
//通过y柱子将x柱子的盘子移到z柱子,并且使用n来控制函数体的书写
1、我们将A柱子(n-1)个盘子移到B柱子
dfs(a,b,c,n-1)2、再将A柱子下面的最后一盘移到C柱子
c.push_back(a.back());
a.pop_back();3、再将B柱子的(n-1)个盘子移到C柱子
dfs(b,a,c,n-1);终止条件
当A只有一个盘子时候,就终止了
if (n == 1)
{
c.push_back(a.back());
a.pop_back();
return ;
}
以上思路就讲解完了,大家可以先自己先做一下
代码实现
class Solution {
public:
void dfs(vector<int>& x, vector<int>& y, vector<int>& z,int n)
{
if (n == 1)
{
z.push_back(x.back());
x.pop_back();
return ;
}
dfs(x,z,y,n-1);
z.push_back(x.back());
x.pop_back();
dfs(y,x,z,n-1);
}
void hanota(vector<int>& A, vector<int>& B, vector<int>& C)
{
int n = A.size();
dfs(A,B,C,n);
}
};