更多资料获取
📚 个人网站:ipengtao.com
在机器学习和数据科学领域,理解特征在模型中的重要性对于构建准确且可靠的预测模型至关重要。Python提供了多种强大的工具和技术,能够探索特征重要性的各个方面。
本文将详细介绍8种常用的方法,涵盖了基于决策树、集成学习模型以及统计学方法的特征重要性分析。从决策树模型到SHAP值,将深入探讨每种方法的原理和示例代码,帮助全面了解如何评估特征的重要性。通过综合运用这些技术,将能更好地理解特征对模型预测的贡献,为提升模型性能和解释模型决策提供有力支持。
决策树模型方法
1. 特征重要性分析
决策树模型通过特征分裂过程来评估特征的重要性。可以使用DecisionTreeClassifier或DecisionTreeRegressor来获得特征的重要性评分。
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 加载数据集
data = load_iris()
X = data.data
y = data.target
# 构建决策树模型
model = DecisionTreeClassifier()
model.fit(X, y)
# 获取特征重要性
importance = model.feature_importances_
# 特征重要性可视化
plt.barh(range(X.shape[1]), importance, align='center')
plt.yticks(range(X.shape[1]), data.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Features')
plt.show()
2. 使用Random Forest进行特征重要性分析
Random Forest是集成学习模型,它可以提供更为稳健的特征重要性评分。
from sklearn.ensemble import RandomForestClassifier
# 构建Random Forest模型
rf_model = RandomForestClassifier()
rf_model.fit(X, y)
# 获取特征重要性
importance_rf = rf_model.feature_importances_
# 可视化Random Forest的特征重要性
plt.barh(range(X.shape[1]), importance_rf, align='center')
plt.yticks(range(X.shape[1]), data.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Features')
plt.show()
统计学方法
3. 使用Pearson相关系数
Pearson相关系数可以衡量特征之间的线性关系。
import pandas as pd
# 创建DataFrame
df = pd.DataFrame(data.data, columns=data.feature_names)
df['target'] = data.target
# 计算Pearson相关系数
correlation = df.corr()
# 可视化相关系数矩阵
import seaborn as sns
plt.figure(figsize=(10, 8))
sns.heatmap(correlation, annot=True, cmap='coolwarm')
plt.title('Pearson Correlation Matrix')
plt.show()
4. 使用互信息
互信息衡量的是两个变量之间的不确定性减少程度。
from sklearn.feature_selection import mutual_info_classif
# 计算互信息
mi = mutual_info_classif(X, y)
# 可视化互信息
plt.barh(range(X.shape[1]), mi, align='center')
plt.yticks(range(X.shape[1]), data.feature_names)
plt.xlabel('Mutual Information')
plt.ylabel('Features')
plt.show()
统计学方法与模型解释性
5. 使用SHAP值(SHapley Additive exPlanations)
SHAP是一种现代化的、模型无关的特征重要性评估方法。它可以为模型预测结果解释每个特征的贡献度。
import shap
# 创建并训练一个模型(例如XGBoost)
model = xgb.XGBClassifier()
model.fit(X, y)
# 创建一个SHAP解释器
explainer = shap.Explainer(model)
shap_values = explainer.shap_values(X)
# 可视化SHAP值
shap.summary_plot(shap_values, X, feature_names=data.feature_names, plot_type="bar")
6. Permutation Feature Importance
该方法通过随机地打乱特征值,观察这种打乱对模型性能的影响来计算特征重要性。
from sklearn.inspection import permutation_importance
# 计算Permutation Feature Importance
result = permutation_importance(model, X, y, n_repeats=10, random_state=42)
# 可视化Permutation Feature Importance
sorted_idx = result.importances_mean.argsort()
plt.barh(range(X.shape[1]), result.importances_mean[sorted_idx], align='center')
plt.yticks(range(X.shape[1]), data.feature_names[sorted_idx])
plt.xlabel('Permutation Importance')
plt.ylabel('Features')
plt.show()
其他方法
7. 使用GBDT(Gradient Boosting Decision Tree)
GBDT可以提供各个特征在模型中的分裂度。
from sklearn.ensemble import GradientBoostingClassifier
# 构建GBDT模型
gbdt_model = GradientBoostingClassifier()
gbdt_model.fit(X, y)
# 获取特征重要性
importance_gbdt = gbdt_model.feature_importances_
# 可视化GBDT的特征重要性
plt.barh(range(X.shape[1]), importance_gbdt, align='center')
plt.yticks(range(X.shape[1]), data.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Features')
plt.show()
8. 使用XGBoost
XGBoost是一种梯度提升算法,也可以用于特征重要性分析。
import xgboost as xgb
# 转换数据为DMatrix格式
dtrain = xgb.DMatrix(X, label=y)
# 定义参数
param = {'objective': 'multi:softmax', 'num_class': 3}
# 训练模型
num_round = 10
xgb_model = xgb.train(param, dtrain, num_round)
# 可视化特征重要性
xgb.plot_importance(xgb_model)
plt.show()
总结
这些方法为理解特征在模型中的重要性提供了多种视角。决策树和集成学习模型提供了直接的特征重要性分析,而统计学方法(如相关系数、互信息)可用于了解特征之间的关系。同时,SHAP值和Permutation Feature Importance提供了模型预测的个性化解释和对特征重要性的直观理解。
综合使用这些方法可以更全面地评估特征的重要性,并且为模型解释提供更深入的认识。在实际应用中,根据数据集的特性和所使用的模型,选择适当的方法来进行特征重要性分析是至关重要的。
这些方法和示例代码将帮助你更好地理解特征重要性分析,并为你的机器学习项目提供有力支持。
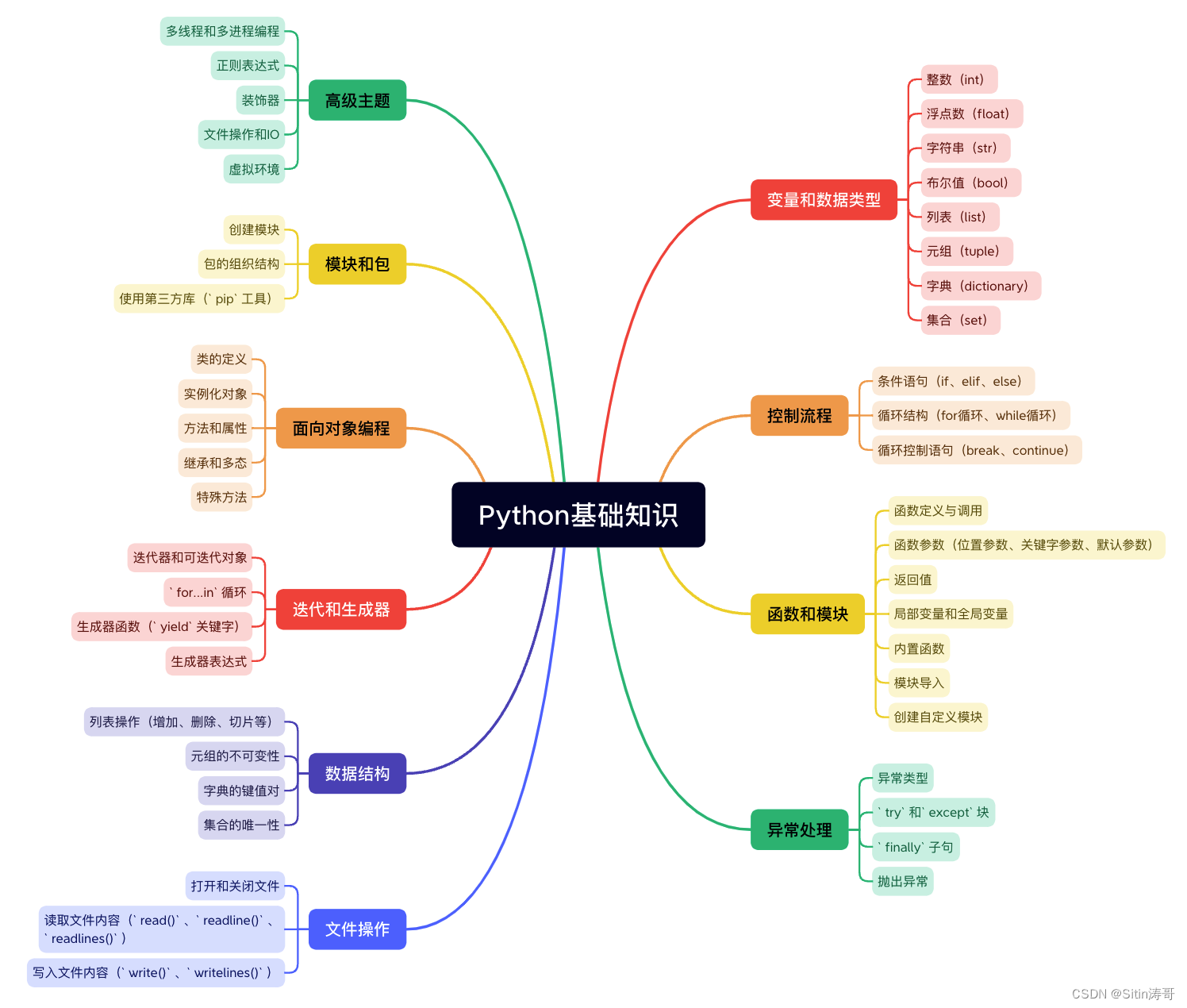
Python学习路线
更多资料获取
📚 个人网站:ipengtao.com
如果还想要领取更多更丰富的资料,可以点击文章下方名片,回复【优质资料】,即可获取 全方位学习资料包。

点击文章下方链接卡片,回复【优质资料】,可直接领取资料大礼包。