一、堆树

1、定义

堆树的定义如下：
（1）堆树是一颗完全二叉树。
（2）堆树的每一个结点值都大于等于或者小于等于其左右子结点的值。
（3）堆树中每个结点的子树都是堆树。

为什么是大于等于或者小于等于呢？

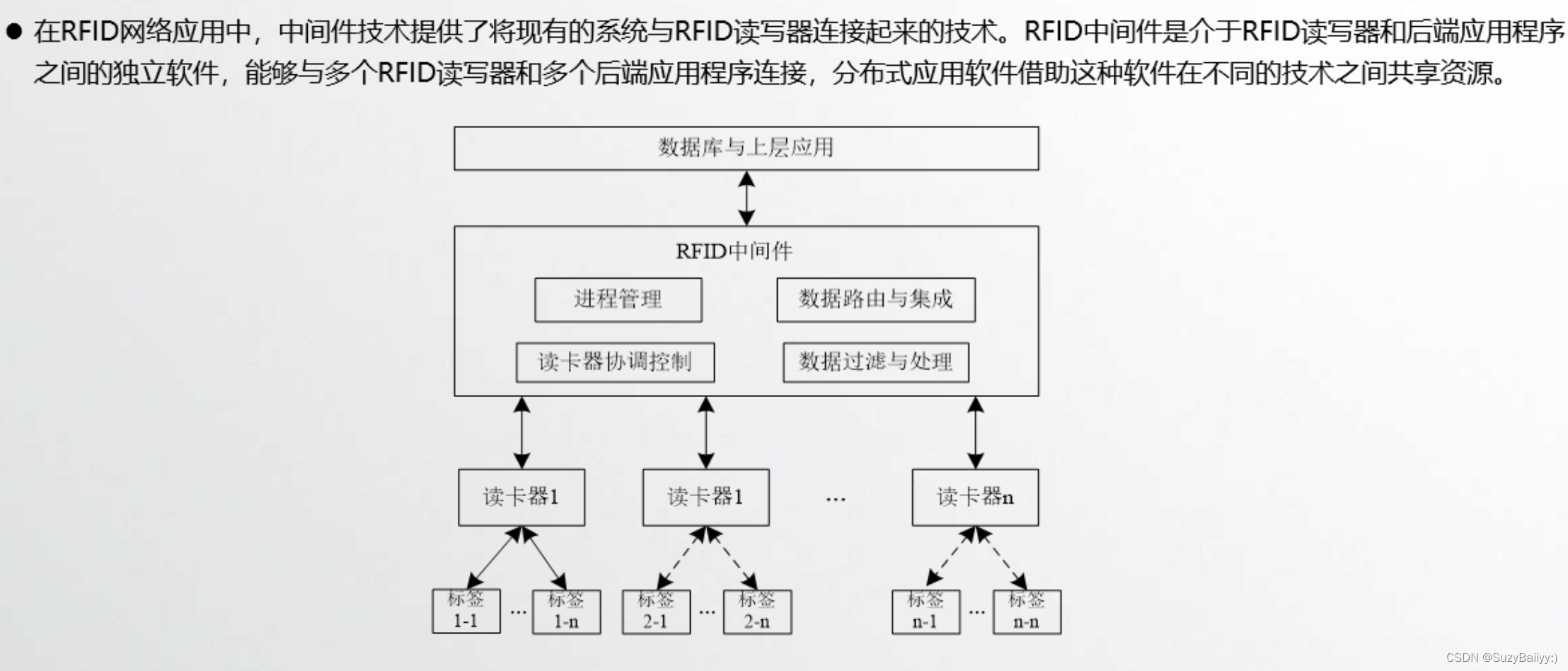
• 如果值都大于等于，那么根就是最大的数，这样的堆树可以称为大顶堆。
• 如果值都小于等于，那么根就是最小的数，这样的堆树可以称为小顶堆。

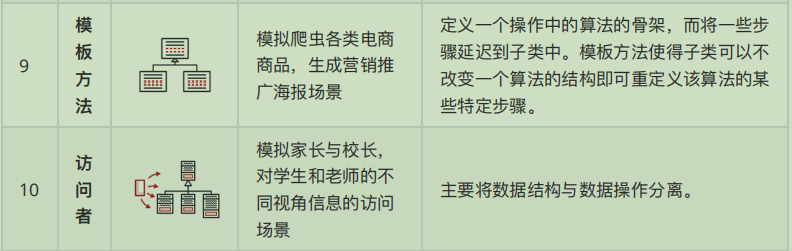
如下图所示（图来自网络）：

2、堆树是如何来存储的？

完全二叉树：除了最后一层，其他层每个结点都是满的，并且最后一层的结点全部靠左排列。

完全二叉树的最佳存储结构就是数组。因为它有着特殊的属性，直接利用下标就可以表示左右结点。

所以，堆树也可以很方便的用数组来存储表示：

假设下标从0开始，如果父结点索引是 i，那么它两个子结点的索引就是 2i+1和 2i+2。

3、堆树的操作

3.1 插入操作

堆的插入有两种实现方式：

• （1）从下往上
• （2）从上往下

堆树插入之后要进行一个堆化的操作，也就是让这棵树满足堆树的性质。
其插入过程就叫做堆化。

（1）从下往上

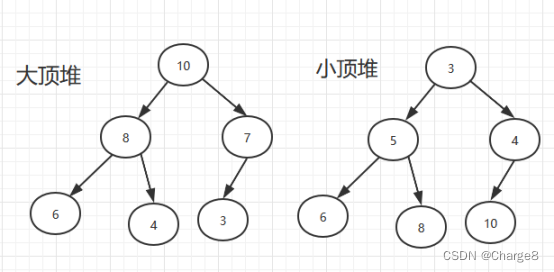
因为完全二叉树用数据构造之后，那么新插入的数据都在最后，但是插入之后，可能就不满足堆树的要求了，所以需要进行变动。以上图的大顶堆为例，

从下往上：我们在最后插入9之后是不满足堆树的性质的，所以我们需要与其父结点进行交换，直到依次往上做到不能交换位置为止。

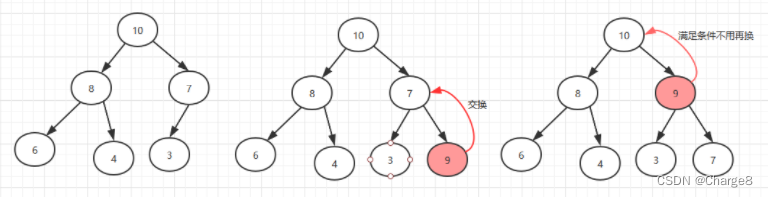
（2）从上往下

从上往下：其实就是把插入的点放到堆顶，然后依次往下比较交换即可。

3.2 删除操作

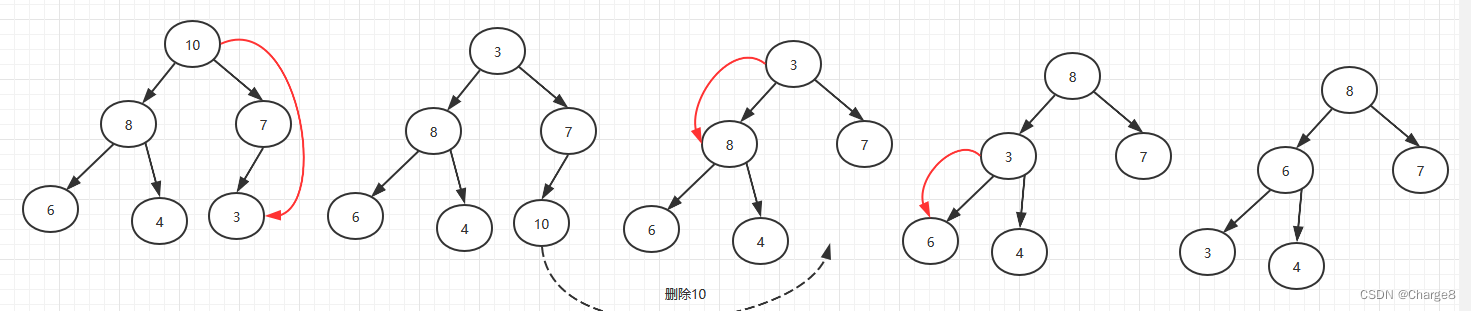
假设我们要删除掉根结点10，并且删除之后，如何才能删除之后还能满足堆树的性质呢？

其实就是将要删除的元素和最后一个元素交换之后，然后删除最后一个元素之后，最后再从上往下进行堆化的操作即可。

3.3 修改操作

修改数据之后，同样要进行堆化操作，根据修改之后的数据和他父结点和子结点比较来决定是向上还是向下进行堆化操作。

二、堆排序算法

1、堆排序算法简介

堆排序（Heap Sort）：是指利用堆树（大顶堆、小顶堆）这种数据结构所设计的一种排序算法。

堆树是一个完全二叉树的结构，并同时满足如下性质：即它的每一个子结点的键值或索引总是小于（或者大于）它的父结点。

堆排序算法演示动画：https://www.cs.usfca.edu/~galles/visualization/HeapSort.html

1.1 基本思想

堆排序的基本思想：就是先将数组序列构造成堆树，再进行排序。

那么怎么将一个数组序列构造成堆树？

1. 先按照序列顺序存储在完全二叉树中（建堆）。
2. 从最后一个非叶子节点从下往上堆化（得到堆树）。
   因为最后一个叶子节点没必要堆化。最后一个叶子结点的父结点就是最后一个非叶子结点。
3. 将堆首和堆尾元素进行交换，交换之后进行一次堆化，依次进行这个操作即可完成排序。

注意：堆排序完全依赖于大顶堆（小顶堆）的相关操作。

运行过程图如下：

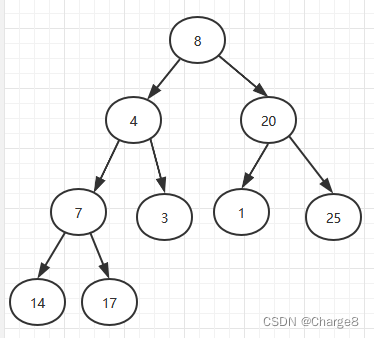
比如：这个数组：[8 4 20 7 3 1 25 14 17]。

1）完全二叉树结构：

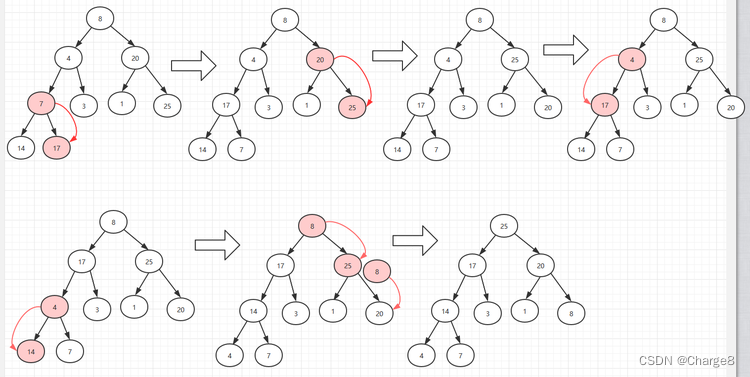
2）大顶堆的构建：假设构建大顶堆：

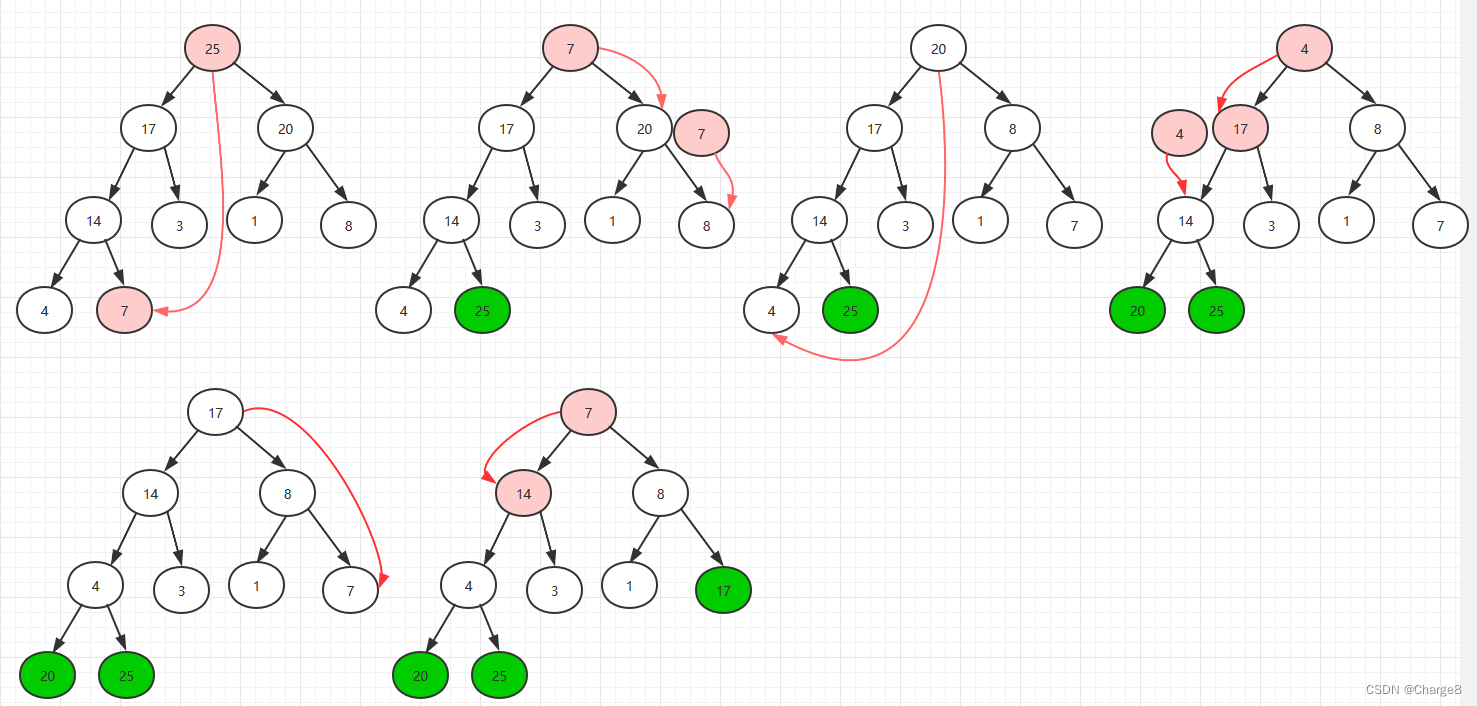
3）堆排序过程：

1.2 性能分析

• 堆排序的时间复杂度为：O(nlogn)；
• 空间复杂度为：O(1)；
• 堆排序是不稳定的排序算法。

2、代码实现

1）实现数组序列转堆树和堆排序：

public class HeapSort {

	/**
	 * 堆排序
	 * @param arr
	 */
	public static void heapSort(int[] arr) {
		int len = arr.length;
		/**
		 * 数组构造堆树，从倒数第一个非叶子结点开始从下往上依次进行堆化操作。<br/>
		 * 索引从0开始。两个子结点索引是 2i+1和 2i+2，所以最后一个非叶子结点的索引就是 len/2 - 1
		 */
		for (int i = len / 2 - 1; i >=0 ; i--) { //时间复杂度nlogn
			createMaxHeap(arr, i, len);
		}

		for (int i = len - 1; i > 0 ; i--) { //时间复杂度nlogn
			int maxData = arr[0]; //第一个数最大
			arr[0] = arr[i];
			arr[i] = maxData;
			/**
			 * 交换堆首和堆尾元素，然后重新构造大顶堆。
			 * 最后到 i为止都是排好序的，堆化的时候不需要再操作了
			 */
			createMaxHeap(arr, 0, i); // 因为 len~i 已经排好序了。每循环一次就构造好了排好序的数的位置，
		}
	}

	/**
	 * 大顶堆构造及堆化过程
	 * @param arr
	 * @param start - 每次都从堆顶开始
	 * @param end  - end之后是已经排好序的，所以需要end下标来判断结束
	 */
	public static void createMaxHeap(int[] arr, int start, int end) {
		int parentIndex = start;
		// 左子结点（下标是从0开始的就要加1）
		int leftChildIndex = 2 * parentIndex + 1;
		while (leftChildIndex < end) {
			// temp表示: 左右左结点，最大的那一个。
			int tempIndex = leftChildIndex;
			//比较左右结点谁大，记录谁的下标
			if (leftChildIndex + 1 < end && arr[leftChildIndex] < arr[leftChildIndex + 1]) {
				tempIndex = leftChildIndex + 1;
			}
			//父结点比孩子大，不交换
			if (arr[parentIndex] > arr[tempIndex]) {
				return;
			}else { //交换数据，刷新父结点继续执行堆化操作
				int tempData = arr[parentIndex];
				arr[parentIndex] = arr[tempIndex];
				arr[tempIndex] = tempData;
				parentIndex = tempIndex; // 继续堆化
				leftChildIndex = 2 * parentIndex + 1;
			}
		}
	}
	
}

2）测试

    public static void main(String[] args) {
        int data[] = { 8, 4, 20, 7, 3, 1, 25, 14, 17 };

        HeapSort.heapSort(data);
        System.out.println(Arrays.toString(data));
    }

参考文章：

• 高级数据结构—堆树和堆排序：https://www.cnblogs.com/nijunyang/p/12820356.html

– 求知若饥，虚心若愚。