Python量化交易06——Fama-French三因子模型(Rmt,SMB,HML)

参考书目:深入浅出Python量化交易实战

本次带来的是著名的获得了诺贝尔奖的三因子模型。

因子模型介绍

Fama和French从可以解释股票收益率的众多因素中提取出了三个重要的影响因子，即市场风险溢酬因子、市值因子和账面市值比因子B/M Ratio，仿照CAPM模型用这三个因子建立起来一个线性模型来解释股票的收益率，这就是著名的三因子模型（Fama and French Three Factor Model，简称FF3）。

三因子模型中的3个因子均为投资组合的收益率：
市场风险溢酬因子(Rmt)对应了（市场投资组合的收益率减去无风险利率）；

市值因子(SMB)对应了做多市值较小的公司与做空市值较大的公司的投资组合带来的收益率；

账面市值比因子(HML)对应的是做多高BM公司、做空低BM公司的投资组合带来的收益率。

三因子模型的形式为：

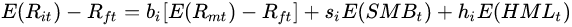
其中SMB（Small Minus Big）为市值因子，也就是小公司比大公司高出的收益率，HML（High Minus Low）代表账面市值比因子，用高B/M比股票减去低B/M比股票的收益率得到； $b_{i}$ $s_{i}$ $h_{i}$ 分别为投资组合（或单只股票）的收益率对三个因子的敏感系数。

实证模型上常用：

来做回归检验，公式中 $\alpha _{i}$ 就是我们通常说的超额收益率。在进行实证研究时，投资组合（或个股）收益率Rit、无风险利率 Rft、市场投资组合Rmt、市值因子SMBt和账面市值比因子组合HMLt都是已知的，通过线性回归拟合最小化残差平方和我们可以得到参数 $\alpha _{i}$ , $b_{i}$ , $s_{i}$ , $h_{i}$ 的估计值，检验超额收益及三个因子的系数是否显著地异于0，也就是检验三个因子是否能够届时收益率。

这里的 $\alpha _{i}$ 和 $\beta _{i}$ 就是我们平时买基金看到的阿尔法和贝塔值，说起来很神秘，其实就是一个回归的截距和系数。整体的三因子模型，说白了就是三元线性回归，最小二乘就能求解的那种。

三因子四因子五因子，就是用3个X，4个X，5个X进行回归。变量X分别是

FF三因子：SMB HML MKT
Carhart四因子：SMB HML MKT UMD
FF五因子：SMB HML MKT RMW CMA

因子数据获取

知道了因子模型的真实面目后，那么这些X怎么来？

一般大型数据公司都会计算好了，直接用就行。我这里找了一个央财的金融院的因子模型的数据，有安装日期，也有周，月，年的数据。本文使用的日期性数据。

链接：五因子数据的更新（2022年10月份数据）-中央财经大学金融学院 (cufe.edu.cn)

唯一的缺点是，只更新到22年10月...没有很及时更新，后续更新可以继续关注央财金融院官网。

数据读取

先导入常用的包

import baostock as bs
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams ['font.sans-serif'] ='SimHei'               #显示中文
plt.rcParams ['axes.unicode_minus']=False               #显示负号

读取因子数据，选取需要的三因子：

factors = pd.read_csv('fivefactor_daily.csv', index_col = 'trddy',parse_dates=['trddy'])
factors = factors[['mkt_rf','rf','smb','hml']].copy()
three_factors = factors['2021-11-01':'2022-11-1']
three_factors.head()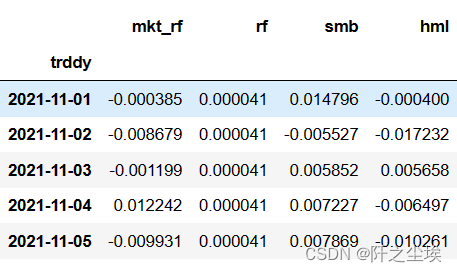

变量名称说明:
trdyr trdwk trdmn trddy [交易日期]
mkt_rf [市场风险因子]
smb [规模风险因子]
hml [账面市值比风险因子]

这里选取了2021年11月到2022年11月的数据。

利用证券宝获取需要分析的股票收盘价数据，这里选择使用中国平安作为样例，同样也是时间为2021年11月到2022年11月的数据。

lg = bs.login()
# 获取沪深A股601318的历史K线数据
rs_result = bs.query_history_k_data_plus("sh.601318",  fields="date,open,high,low,close,volume",   
                        start_date='2021-11-01',   end_date='2022-11-1',  
                        frequency="d",  adjustflag="3")
df_result = rs_result.get_data()
bs.logout()
df_result=df_result.set_index('date')
df_result=df_result.astype('float64')
df_result.head()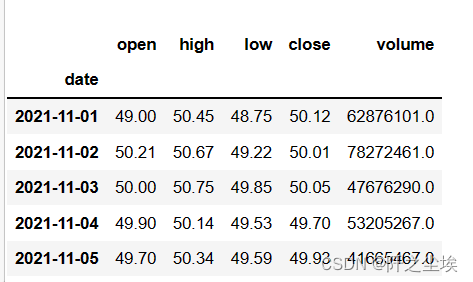

查看一下数据的长度

len(three_factors),len(df_result)

是一样长的，一年大概244个交易日。

收益率计算分析

#计算对数收益率，画图查看

day_return = np.log(df_result['close'] /df_result['close'].shift(1))
day_return.dropna(inplace = True)
day_return.name = 'Return'
day_return.plot(figsize=(7,3))
plt.title('中国平安日收益率')
plt.show()

将因子数据和每日的对数收益率合并

zgpa_threefactor = pd.merge(three_factors, day_return,left_index=True, right_index=True)
zgpa_threefactor.head()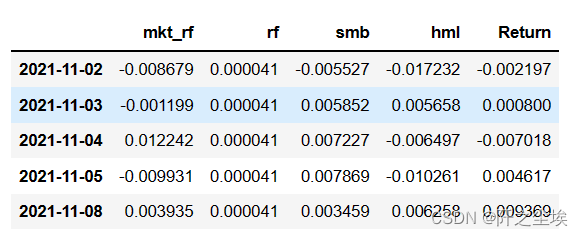

画散点图进行分析

sns.pairplot(zgpa_threefactor[['mkt_rf','smb','hml','Return']])

可以看到收益率和其他三个因子其相关性可能没有那么明显呈现线性关系。

计算相关系数，画热力图

 sns.heatmap(zgpa_threefactor[['mkt_rf','smb','hml','Return']].corr(),annot=True,square=True)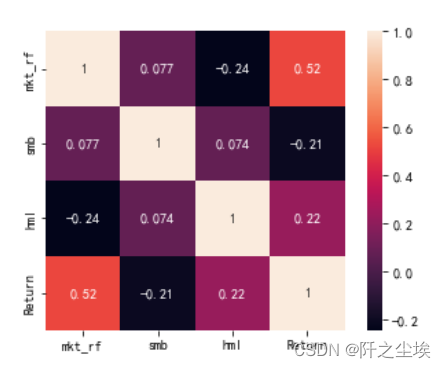

相关性都一般，收益率和Rmt这个因子相关性较大一点。

回归模型

import statsmodels.api as sm
result = sm.OLS(zgpa_threefactor['Return'], sm.add_constant(zgpa_threefactor.loc[:,['mkt_rf','smb','hml']])).fit()
result.summary()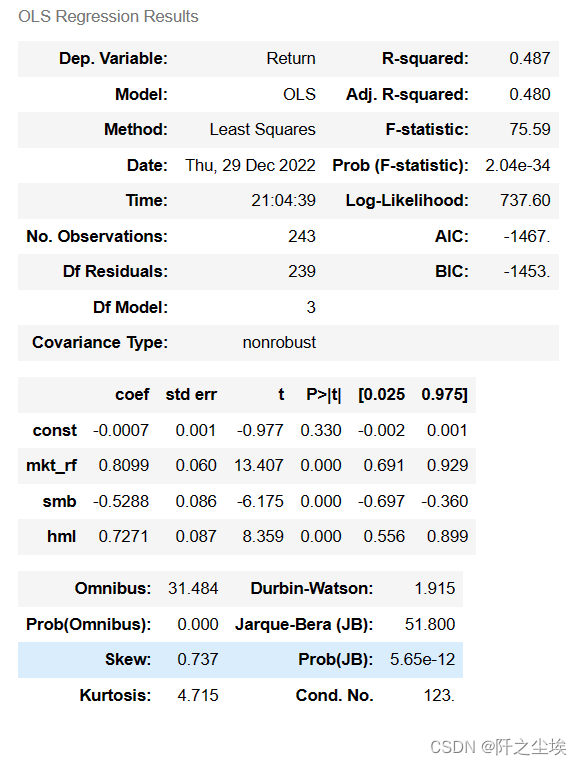

可以看到除了截距，其他三个因子的系数都是显著的。

返回系数列表

list(result.params)

带入模型

可以得到最终计算的模型结果为：

Ri-0.000041=-0.0007+0.8099mkt_rf-0.5288SMB+0.7271hml

其他指标计算

评价一个投资收益有很多指标，其中总收益率，最大回测率，夏普比率，信息比率是常用的四个指标，其计算公式分别为：

策略收益：也就是总收益率，这是最基础的指标，金融中我们也叫单期简单收益率，衡量回测期间策略收益率的。简单说就是期末资产额减去起始资产额再除以起始资产额，这里用了资产意思就是包括现金和持有的股票的价值。

最大回撤：最大回撤率是一个衡量策略风险的重要指标，越小越好

夏普比率：表示每承受一单位总风险，会产生多少的超额报酬，肯定是越大越好。夏普比率是在资本资产定价模型进一步发展得来的。

信息比率：衡量单位超额风险带来的超额收益。信息比率越大，说明该策略单位跟踪误差所获得的超额收益越高，因此，信息比率较大的策略的表现要优于信息比率较低的基准。合理的投资目标应该是在承担适度风险下，尽可能追求高信息比率。

代码为：

def sum_return_ratio(price_list):
    '''实际总收益率'''
    price_list=price_list.to_numpy()
    return (price_list[-1]-price_list[0])/price_list[0]
def MaxDrawdown(price_list):
    '''最大回撤率'''
    i = np.argmax((np.maximum.accumulate(price_list) - price_list) / np.maximum.accumulate(price_list))  # 结束位置
    if i == 0:
        return 0
    j = np.argmax(price_list[:i])  # 开始位置
    return (price_list[j] - price_list[i]) / (price_list[j])
def sharpe_ratio(price_list,rf=0.000041):
    '''夏普比率'''
    #公式 夏普率 = (回报率均值 - 无风险率) / 回报率的标准差
    # pct_change()是pandas里面的自带的计算每日增长率的函数
    daily_return = price_list.pct_change()
    return daily_return.mean()-rf/ daily_return.std()
def Information_Ratio(price_list,rf=0.000041):
    '''信息比率'''
    chaoer=sum_return_ratio(price_list)-((1+rf)**365-1)
    return chaoer/np.std(price_list.pct_change()-rf)

计算上述的中国平安的相应的四个指标为：

sum_return_ratio(df_result['close']),MaxDrawdown(df_result['close']),sharpe_ratio(df_result['close']),Information_Ratio(df_result['close'],rf=0.000041)

多公司对比

将上述流程推广为更加一般的形式，定义一个函数，输入证券代码和开始结束日期，就能自动计算出这些因子的bata系数和这些指标：

def deal(stock='sh.601318',start_date='2021-11-01',end_date='2022-11-1'):
    lg = bs.login()
    rs_result = bs.query_history_k_data_plus(stock,  fields="date,close", start_date=start_date,end_date=end_date, frequency="d", adjustflag="3")
    df_result = rs_result.get_data()
    df_result=df_result.set_index('date')
    df_result=df_result.astype('float64')
    bs.logout()
    three_factors = factors[start_date:end_date]
    assert len(three_factors)==len(df_result), "数量长度不一样" 
    
    day_return = np.log(df_result['close'] /df_result['close'].shift(1))
    day_return.dropna(inplace = True)
    day_return.name = 'Return'
    zgpa_threefactor = pd.merge(three_factors, day_return,left_index=True, right_index=True)
    result = sm.OLS(zgpa_threefactor['Return'], sm.add_constant(zgpa_threefactor.loc[:,['mkt_rf','smb','hml']])).fit()
    betas=result.params
    实际总收益率=sum_return_ratio(df_result['close'])
    最大回测率=MaxDrawdown(df_result['close'])
    夏普比率=sharpe_ratio(df_result['close'])
    信息比率=Information_Ratio(df_result['close'])
    return pd.DataFrame({'阿尔法':betas[0],'贝塔':betas[1],'市值因子SMB':betas[2],'账面市值因子HML':betas[3],
                        '实际总收益率':实际总收益率,'最大回测率':最大回测率,'夏普比率':夏普比率,'信息比率':信息比率},index=[stock])

我们拿贵州茅台去试试：

deal(stock='sh.600519')

可以返回上面的说的所有指标。

这样就能写循环，计算你所有想计算的股票了。

stocks=['sh.601318','sh.600519','sh.600416','sh.600765','sh.600535','sz.300129','sh.600036','sz.000001']
df_deals=pd.DataFrame()
for s in stocks:
    df_deal=deal(stock=s)
    df_deals=pd.concat([df_deals,df_deal],axis=0)

计算了上述8家公司