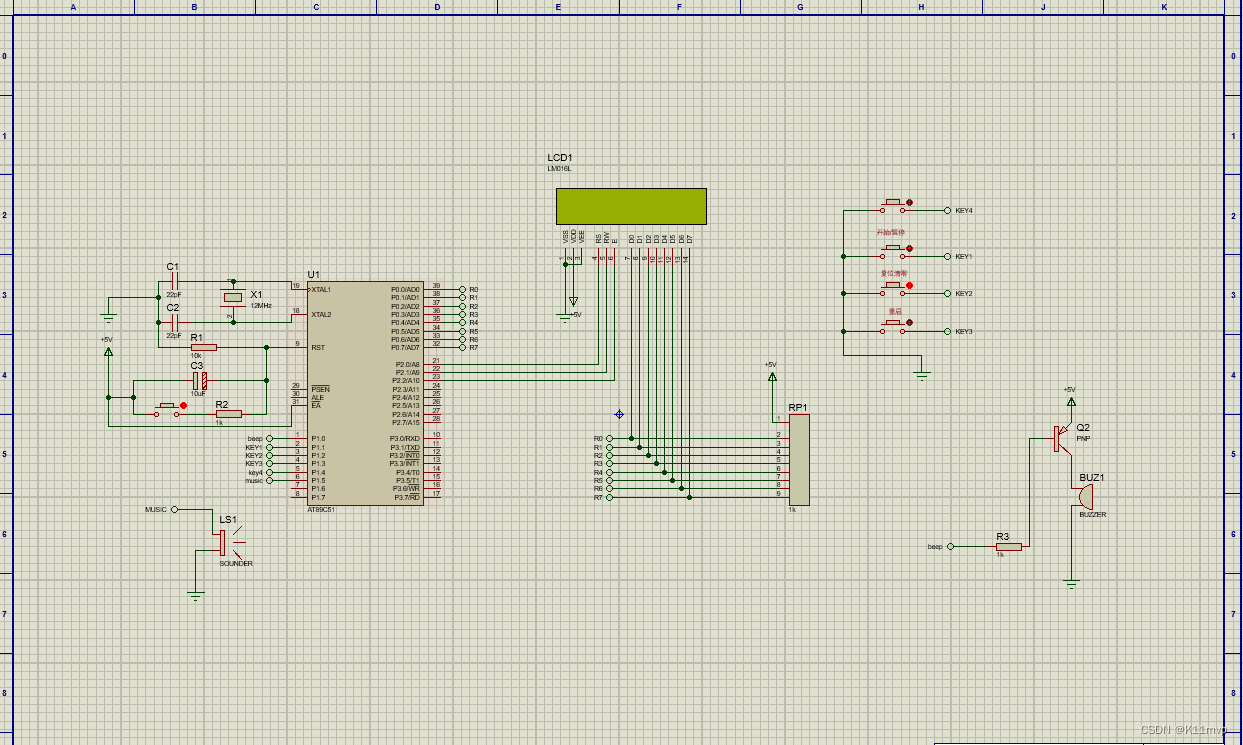
Course1-Week3-分类问题
文章目录
- Course1-Week3-分类问题
- 1. 逻辑回归
- 1.1 线性回归不适用于分类问题
- 1.2 逻辑回归模型
- 1.3 决策边界
- 2. 逻辑回归的代价函数
- 3. 实现梯度下降
- 4. 过拟合与正则化
- 4.1 线性回归和逻辑回归中的过拟合
- 4.2 解决过拟合的三种方法
- 4.3 正则化
- 4.4 用于线性回归的正则方法
- 4.5 用于逻辑回归的正则方法
- 笔记主要参考B站视频“(强推|双字)2022吴恩达机器学习Deeplearning.ai课程”。
- 本篇笔记对应课程 Course1-Week3(下图中深紫色)。

1. 逻辑回归
1.1 线性回归不适用于分类问题
概念明晰:
- 本课程中,class/category两者都表示“分类问题”的输出类别,两者意义相同。
- “逻辑回归(logistic regression)算法”用来解决“分类问题(classfication)”。这是历史遗留的命名问题。
本周将学习“分类问题”,其 输出为有限取值,而不是某段范围内无限的数字。若分类问题的输出结果只有两种可能的分类/类别(class/category),就被称为“二元分类(binary classfication)”,比如下面的三个问题:
- 是否为垃圾邮件?(0/1)
- 是否为交易欺诈?(0/1)
- 是否为恶性肿瘤?(0/1)下图与Week1“肿瘤分类”示意图的不同,仅在于下图画出了实际的纵轴。
惯例:0表示“否”,1表示“是”。0/1 只有 否定/肯定 含义,并不具有褒贬含义。
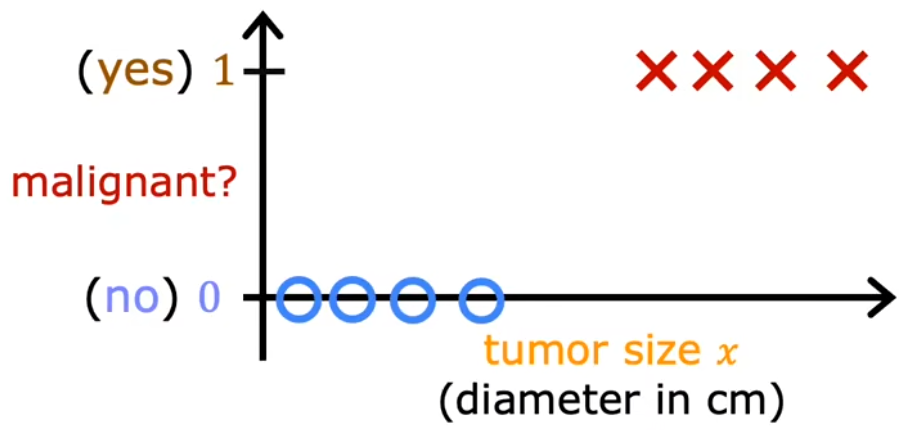
若我们采用前面学过的“线性回归”,对于特定的训练集(没有最右侧样本),看起来是合理的。因为此时以0.5作为阈值,其与样本拟合线(蓝色)相交在横轴上的点,便可以作为一个边界(蓝色),边界左侧都是良性(0),边界右侧都是恶性(1)。但此时额外添加一个最右侧的样本,显然拟合线(绿色)和横轴上的边界(绿色)都和预期不符:

- 决策边界(decision boundary):横轴上的边界。
总的来说,有时候可以很幸运地使用“线性回归”解决“分类问题”,但大多数情况下都不行,线性拟合不适用于分类问题。于是下面将介绍“逻辑回归(logistic regression)”,来解决分类问题,这也是一种当今被广泛使用的算法。
1.2 逻辑回归模型
弹幕注:“逻辑回归”在西瓜书上被写作“对数几率回归”。
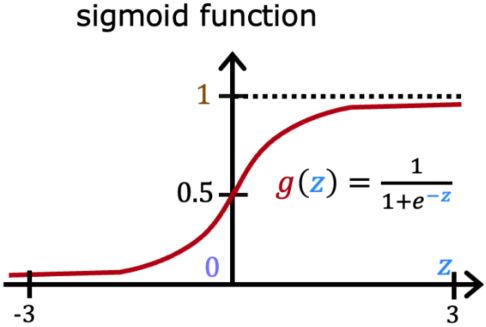
“逻辑回归”是一种当今被广泛使用的算法,比如生活中的“精准广告投放”算法,老师说他在工作中也经常用。“逻辑回归(logistic regression)”使用S型曲线来进行函数拟合,最常见的S型曲线就是 Sigmoid function,其也被称为 logistic function:

Sigmoid函数: g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1,其性质为:
- 0 < g ( z ) < 1 0 < g(z) < 1 0<g(z)<1
- g ( 0 ) = 0.5 g(0)=0.5 g(0)=0.5
- z z z 越大, g ( z ) g(z) g(z) 越接近1; z z z 越小, g ( z ) g(z) g(z) 越接近0。
只要根据样本的散点图,选择不同的方式对
z
z
z 拟合(见下一小节),就可以解决各种各样的分类问题。比如在“肿瘤分类问题”中,令
z
z
z 为一条直线
z
=
w
⃗
⋅
x
⃗
+
b
z=\vec{w}·\vec{x}+b
z=w⋅x+b,并将其代入到Sigmoid函数中,便可得到“(多元)逻辑回归算法”的数学模型:
Logistic regression model
assume
z
=
w
⃗
⋅
x
⃗
+
b
:
f
w
⃗
,
b
(
x
⃗
)
=
g
(
z
)
=
g
(
w
⃗
⋅
x
⃗
+
b
)
=
1
1
+
e
−
(
w
⃗
⋅
x
⃗
+
b
)
\begin{aligned} \text{Logistic regression model}\\ \text{assume} \; z = \vec{w}·\vec{x}+b \end{aligned} : \quad f_{\vec{w},b}(\vec{x}) = g(z) = g(\vec{w}·\vec{x}+b) = \frac{1}{1+e^{-(\vec{w}·\vec{x}+b)}}
Logistic regression modelassumez=w⋅x+b:fw,b(x)=g(z)=g(w⋅x+b)=1+e−(w⋅x+b)1
对于使用Sigmoid函数构建的“逻辑回归”的数学模型来说,输入相应的特征或特征集,就会输出一个0~1之间的数字,这个输出可以认为是 y = 1 y=1 y=1 的“概率(probability)”: f w ⃗ , b ( x ⃗ ) = P ( y = 1 ∣ x ⃗ ; w ⃗ , b ) f_{\vec{w},b}(\vec{x}) = P(y=1|\vec{x};\vec{w},b) fw,b(x)=P(y=1∣x;w,b)。也就是,在给定参数 w ⃗ \vec{w} w和 b b b、输入 x ⃗ \vec{x} x 的情况下,其输出 y = 1 y=1 y=1 的概率。比如对于上述“肿瘤分类问题”来说,输出的数字就表示“为恶性肿瘤的概率 P ( 1 ) P(1) P(1)”,若输出0.7,则表示该模型认为有70%的可能是恶性肿瘤(30%的可能不是恶性肿瘤)。
1.3 决策边界
前面提到,“逻辑回归”的输出表示“输出为1的概率”。那么很自然的便想到,我们应当选取一个“阈值”,当输出概率大于这个“阈值”时,就可以认为输出结果为1,这个“阈值”就是“决策边界(decision boundary)”。显然,最直观的决策边界就是选取
g
(
z
)
=
0.5
g(z)=0.5
g(z)=0.5,也就是:
f
w
⃗
,
b
(
x
⃗
)
=
g
(
z
)
≥
0.5
⟹
y
^
=
1
f
w
⃗
,
b
(
x
⃗
)
=
g
(
z
)
<
0.5
⟹
y
^
=
0
\begin{aligned} & f_{\vec{w},b}(\vec{x}) = g(z) \ge 0.5 \Longrightarrow \hat{y}=1\\ & f_{\vec{w},b}(\vec{x}) = g(z) < 0.5 \Longrightarrow \hat{y}=0 \end{aligned}
fw,b(x)=g(z)≥0.5⟹y^=1fw,b(x)=g(z)<0.5⟹y^=0
而 “决策边界”的形状则由 z z z 决定,令 z = w ⃗ ⋅ x ⃗ + b z=\vec{w}·\vec{x}+b z=w⋅x+b,决策边界便为一条直线;令 z z z 为更高阶的多项式,则可以得到形状更复杂的决策边界,这便是“逻辑回归”可以学习相当复杂的数据集的奥妙所在。下面是两个示例:
示例1:决策边界为直线
本分类问题令
z
=
w
1
x
1
+
w
2
x
2
+
b
z=w_1x_1+w_2x_2+b
z=w1x1+w2x2+b,假设其参数
w
1
=
w
2
=
1
,
b
=
−
3
w_1=w_2=1,b=-3
w1=w2=1,b=−3、决策边界为
g
(
z
)
=
0.5
g(z)=0.5
g(z)=0.5,于是经过移项可得到决策边界为
x
1
+
x
2
=
3
x_1+x_2=3
x1+x2=3(下图紫色直线),决策边界的下方认为是0、上方认为是1,符合直观:
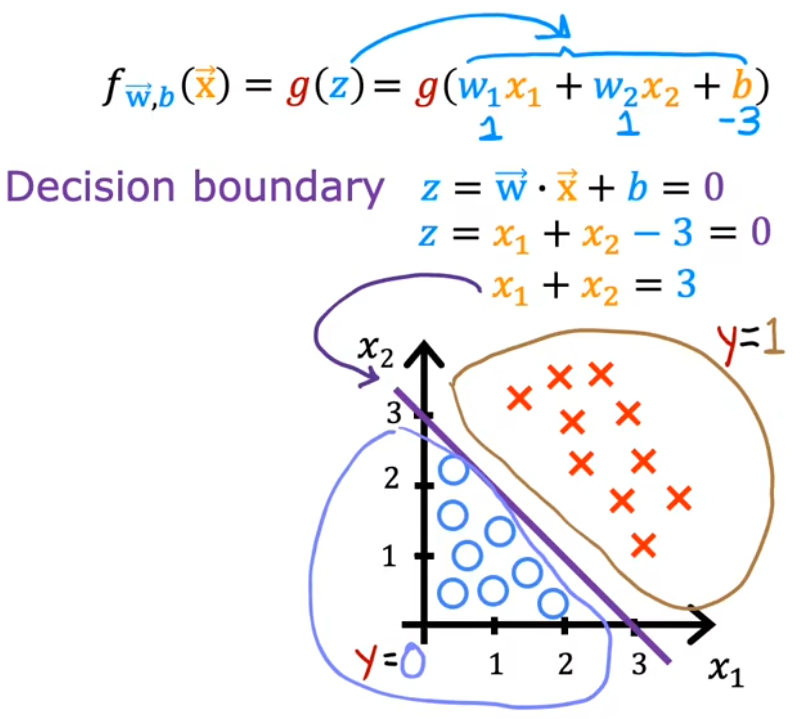
- x 1 x_1 x1、 x 2 x_2 x2表示两种输入特征,红叉表示正向示例(1),蓝圈表示反向示例(0)。
示例2:决策边界为圆
本分类问题令
z
=
w
1
x
1
2
+
w
2
x
2
2
+
b
z=w_1x_1^2+w_2x_2^2+b
z=w1x12+w2x22+b,假设其参数
w
1
=
w
2
=
1
,
b
=
−
1
w_1=w_2=1,b=-1
w1=w2=1,b=−1、决策边界为
g
(
z
)
=
0.5
g(z)=0.5
g(z)=0.5,于是经过移项可得到决策边界为
x
1
2
+
x
2
2
=
1
x_1^{2}+x_2^{2}=1
x12+x22=1(下图紫色圆),决策边界的内部认为是0、外部认为是1,符合直观:

- x 1 x_1 x1、 x 2 x_2 x2表示两种输入特征,红叉表示正向示例(1),蓝圈表示反向示例(0)。
- 平方拟合是因为要构建圆形的方程。
本节 Quiz:
Which is an example of a classification task?
× Based on a patient’s blood pressure, determine how much blood pressure medication (a dosage measured in milligrams) the patient should be prescribed.
√ Based on the size of each tumor, determine if each tumor is malignant (cancerous) or not.
× Based on a patient’s age and blood pressure, determine how much blood pressure medication (measured in milligrams) the patient should be prescribed.Recall the sigmoid function is g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1. If z z z is a large positive number, then:
× g ( z ) g(z) g(z) is near negative one (-1).
× g ( z ) g(z) g(z) will be near zero (0).
√ g ( z ) g(z) g(z) is near one (1).
× g ( z ) g(z) g(z) will be near 0.5.
A cat photo classification model predicts 1 if it’s a cat, and 0 ifit’s not a cat. For a particular photograph, the logistic regression model outputs g ( z ) g(z) g(z) (a number between 0 and 1). Which of these would be a reasonable criteria to decide whether to predict if it’s a cat?
× Predictitis a cat if g ( z ) < 0.5 g(z) < 0.5 g(z)<0.5.
× Predictitis a cat if g ( z ) = 0.5 g(z) = 0.5 g(z)=0.5.
× Predictitis a cat if g ( z ) < 0.7 g(z) < 0.7 g(z)<0.7.
√ Predictitis a cat if g ( 2 ) ≥ 0.5 g(2) \ge 0.5 g(2)≥0.5.
No matter what features you use (including if you use polynomial features), the decision boundary learned by logistic regression will be a linear decision boundary.
√ False
× True
2. 逻辑回归的代价函数
概念明晰:
- 本节中,单个样本使用“损失(loss)函数”,整个训练集使用“代价(cost)函数”。“代价”是所有样本“损失”的平均值。
- 本课程中,若无特殊说明, l o g ( ⋅ ) log(·) log(⋅)函数 都默认对 自然常数 e e e 取对数,即 l o g ( ⋅ ) = l o g e ( ⋅ ) = l n ( ⋅ ) log(·) = log_e(·) = ln(·) log(⋅)=loge(⋅)=ln(⋅)。
和“线性回归”类似,给定“逻辑回归”的模型后,也要讨论一下“逻辑回归”的“代价函数”,用来衡量当前参数对于训练集的匹配程度。在“线性回归”中,我们使用“平方误差”来计算模型的代价函数,但对于“逻辑回归”问题来说,若也采用平方误差函数,那么它的代价函数就如同下图所示,是一个非凸函数,任意一个局部极小值都可能让梯度下降法收敛。显然,“平方误差”不能作为“逻辑回归”的代价函数:
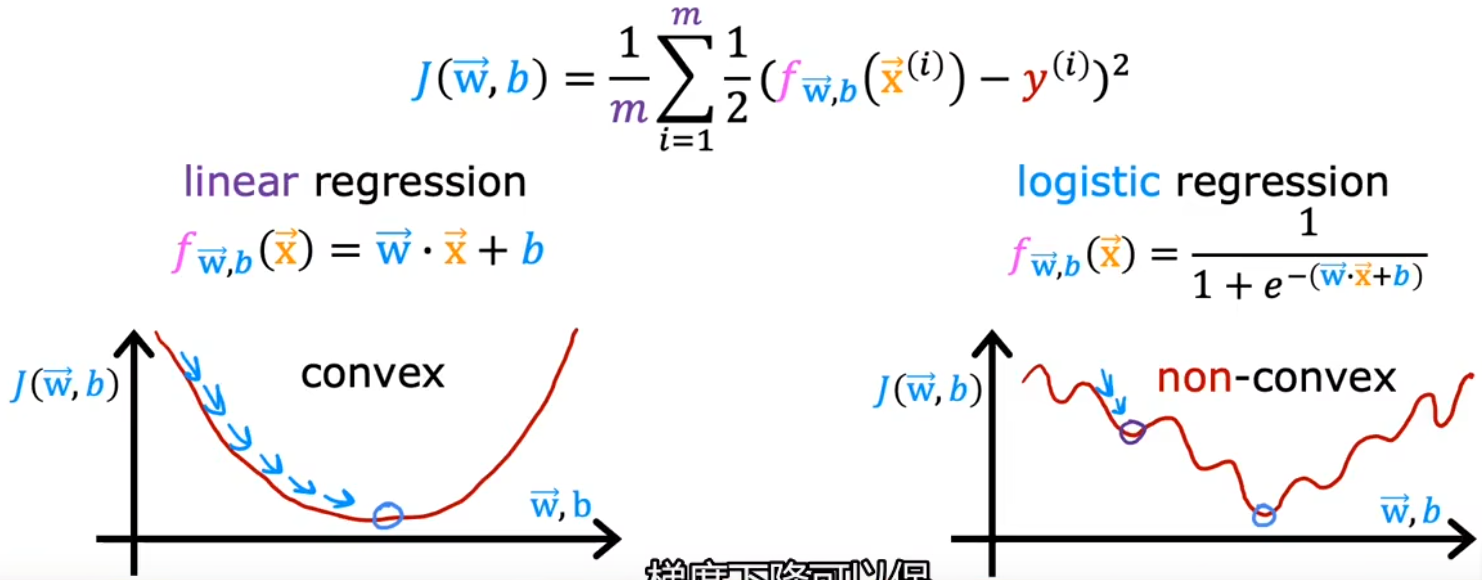
于是定义下面这种形式的 负对数形式的损失函数 L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}) L(fw,b(x(i)),y(i)),进而保证 代价函数 J ( w ⃗ , b ) J(\vec{w},b) J(w,b) 在“逻辑回归”中为凸函数,进而在后续可以使用梯度下降法。下图也给出了使用负对数 − l o g -log −log 作为损失函数的合理性:
Logistic loss function: L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = { − l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) , y ( i ) = 1 , − l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) , y ( i ) = 0. ⇓ Logistic cost function: J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) \begin{aligned} \text{Logistic loss function:}\quad & L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})= \left\{\begin{aligned} -log(f_{\vec{w},b}(\vec{x}^{(i)})), \; &y^{(i)}=1,\\ -log(1-f_{\vec{w},b}(\vec{x}^{(i)})), \; &y^{(i)}=0. \end{aligned}\right.\\ & \Downarrow\\ \text{Logistic cost function:}\quad & J(\vec{w},b) = \frac{1}{m} \sum_{i=1}^{m}L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}) \end{aligned} Logistic loss function:Logistic cost function:L(fw,b(x(i)),y(i))={−log(fw,b(x(i))),−log(1−fw,b(x(i))),y(i)=1,y(i)=0.⇓J(w,b)=m1i=1∑mL(fw,b(x(i)),y(i))
- L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}) L(fw,b(x(i)),y(i)):损失函数,表示单个训练样本 ( x ⃗ ( i ) , y ( i ) ) (\vec{x}^{(i)},y^{(i)}) (x(i),y(i)) 的损失。在“线性回归”中,损失函数为 1 2 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 \frac{1}{2}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2 21(fw,b(x(i))−y(i))2,也就是该样本“平方差损失”的一半。在“逻辑回归”中,损失函数则如上所示。
- 注意 0 < f w ⃗ , b ( x ⃗ ( i ) ) < 1 0 < f_{\vec{w},b}(\vec{x}^{(i)}) < 1 0<fw,b(x(i))<1,所以负对数的形式,可以保证Sigmoid函数越贴近样本,代价越小。
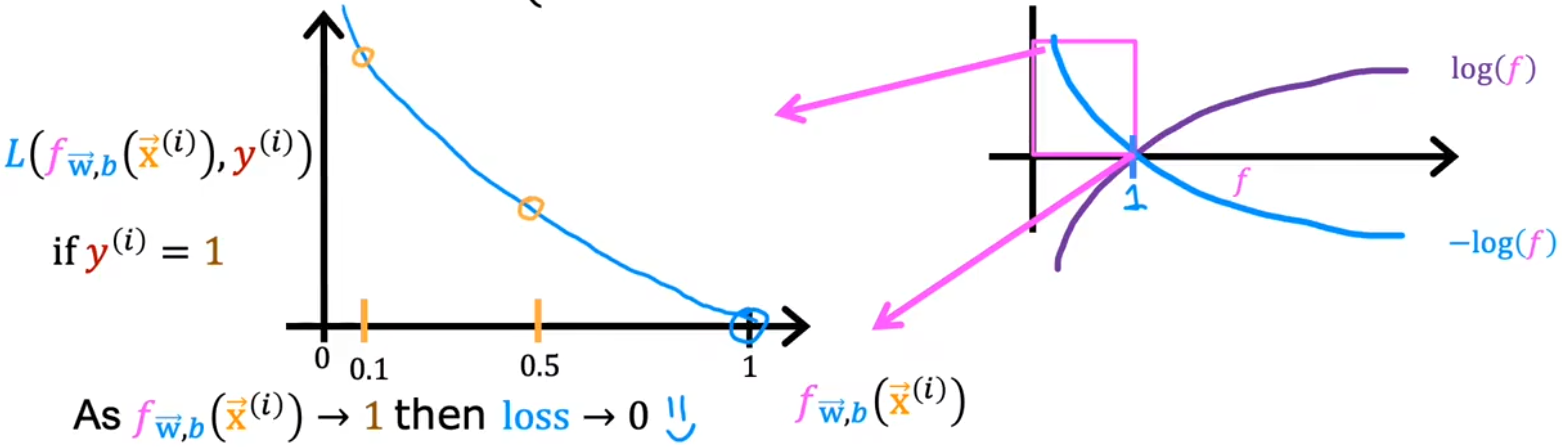

- 预测模型 0 < f w ⃗ , b ( x ⃗ ( i ) ) < 1 0 < f_{\vec{w},b}(\vec{x}^{(i)}) < 1 0<fw,b(x(i))<1。
- 当 y ( i ) = 1 y^{(i)}=1 y(i)=1 时(上左图):预测值 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i)) 越接近1,损失越小甚至趋于0;越远离1,损失函数越大,并且损失的增长速度越来越快,甚至趋于无穷 ∞ \infty ∞。
- 当 y ( i ) = 0 y^{(i)}=0 y(i)=0 时(上右图):预测值 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i)) 越接近0,损失越小甚至趋于0;越远离0,损失函数越大,并且损失的增长速度越来越快,甚至趋于无穷 ∞ \infty ∞。
总结:预测值 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i)) 越接近真实值 y ( i ) y^{(i)} y(i),损失越小趋于0;越远离真实值 y ( i ) y^{(i)} y(i),损失迅速增大趋于 ∞ \infty ∞。
证明这里的损失函数是凸函数超出了本课范畴,我们只需知道上述逻辑回归的“损失函数”和“代价函数”都是凸函数,可以使用梯度下降法找到最小值处的参数值 w ⃗ \vec{w} w和 b b b。并且当前的“肿瘤分类问题”是一个“二元分类问题”, y ( i ) y^{(i)} y(i) 只能取0/1,所以“损失函数”和“代价函数”还可以进一步简化:
Simplified logistic loss function: L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = { − l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) , y ( i ) = 1 , − l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) , y ( i ) = 0. = − y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ⇓ Simplified logistic cost function: J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] \begin{aligned} \text{Simplified logistic loss function:}\quad & \begin{aligned} L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}) & = \left\{\begin{aligned} -log(f_{\vec{w},b}(\vec{x}^{(i)})), \; &y^{(i)}=1,\\ -log(1-f_{\vec{w},b}(\vec{x}^{(i)})), \; &y^{(i)}=0. \end{aligned}\right.\\ & = -y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))-(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)})) \end{aligned}\\ & \Downarrow \\ \text{Simplified logistic cost function:}\quad & \begin{aligned} J(\vec{w},b) &= \frac{1}{m} \sum_{i=1}^{m}L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})\\ &= -\frac{1}{m} \sum_{i=1}^{m}[y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))] \end{aligned} \end{aligned} Simplified logistic loss function:Simplified logistic cost function:L(fw,b(x(i)),y(i))={−log(fw,b(x(i))),−log(1−fw,b(x(i))),y(i)=1,y(i)=0.=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))⇓J(w,b)=m1i=1∑mL(fw,b(x(i)),y(i))=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]
并且从物理意义来讲,上述“代价函数”使用了统计学中“最大似然估计(maximum likehood estimation)”的原理。这只是个特定的代价函数,当然还有其他无数种代价函数。
本节Quiz:
In this lecture series, “cost” and “Ioss” have distinct meanings. Which one applies to a single training example?
√ Loss
× Cost
× Both Loss and Cost
× Neither LOss nor CostFor the simplified loss function, if the label y ( i ) = 0 y^{(i)} = 0 y(i)=0, then what does this expression simplify to?
× l o g ( 1 − f w ⃗ , b ( x ( i ) ) + l o g ( 1 − f w ⃗ , b ( x ( i ) ) ) log(1 - f_{\vec{w},b}(x^{(i)}) + log(1 - f_{\vec{w},b}(x^{(i)})) log(1−fw,b(x(i))+log(1−fw,b(x(i)))
× l o g ( f w ⃗ , b ( x ( i ) ) ) log(f_{\vec{w},b}(x^{(i)})) log(fw,b(x(i)))
√ l o g ( 1 − f w ⃗ , b ( x ( i ) ) ) log(1 - f_{\vec{w},b}(x^{(i)})) log(1−fw,b(x(i)))
× − l o g ( 1 − f w ⃗ , b ( x ( i ) ) ) − l o g ( 1 − f w ⃗ , b ( x ( i ) ) ) -log(1- f_{\vec{w},b}(x^{(i)})) - log(1- f_{\vec{w},b}(x^{(i)})) −log(1−fw,b(x(i)))−log(1−fw,b(x(i)))
3. 实现梯度下降
于是,对上一节给出的“代价函数”进行梯度下降,我们便可以完成整个“逻辑回归”,进而找到最合适的参数
w
⃗
\vec{w}
w和
b
b
b。下面GIF动图给出了“逻辑回归”的完整流程。注意,“逻辑回归”中梯度下降法的表达式仍然和“线性回归”一样(计算上的巧合):
Logistic regression model
:
f
w
⃗
,
b
(
x
⃗
)
=
1
1
+
e
−
(
w
⃗
⋅
x
⃗
+
b
)
Logistic cost function
:
min
w
⃗
,
b
J
(
w
⃗
,
b
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
]
Gradient descent
repeat until convergence
:
{
j
=
1
,
2
,
.
.
.
,
n
.
w
j
=
w
j
−
α
∂
∂
w
j
J
(
w
⃗
,
b
)
=
w
j
−
α
m
∑
i
=
1
m
[
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
⋅
x
⃗
j
(
i
)
]
,
b
=
b
−
α
∂
∂
b
J
(
w
⃗
,
b
)
=
b
−
α
m
∑
i
=
1
m
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
.
\begin{aligned} \text{Logistic regression model} &: \quad f_{\vec{w},b}(\vec{x}) = \frac{1}{1+e^{-(\vec{w}·\vec{x}+b)}}\\ \text{Logistic cost function} &: \quad \min_{\vec{w},b} J(\vec{w},b) = -\frac{1}{m} \sum_{i=1}^{m}[y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))]\\ \begin{aligned} \text{Gradient descent} \\ \text{repeat until convergence} \end{aligned} &: \left\{\begin{aligned} j &= 1,2,...,n.\\ w_j &= w_j - \alpha \frac{\partial }{\partial w_j} J(\vec{w},b) = w_j - \frac{\alpha}{m} \sum_{i=1}^{m}[(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})·\vec{x}^{(i)}_j], \\ b &= b - \alpha \frac{\partial }{\partial b} J(\vec{w},b) = b - \frac{\alpha}{m} \sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)}). \end{aligned}\right. \end{aligned}
Logistic regression modelLogistic cost functionGradient descentrepeat until convergence:fw,b(x)=1+e−(w⋅x+b)1:w,bminJ(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]:⎩
⎨
⎧jwjb=1,2,...,n.=wj−α∂wj∂J(w,b)=wj−mαi=1∑m[(fw,b(x(i))−y(i))⋅xj(i)],=b−α∂b∂J(w,b)=b−mαi=1∑m(fw,b(x(i))−y(i)).
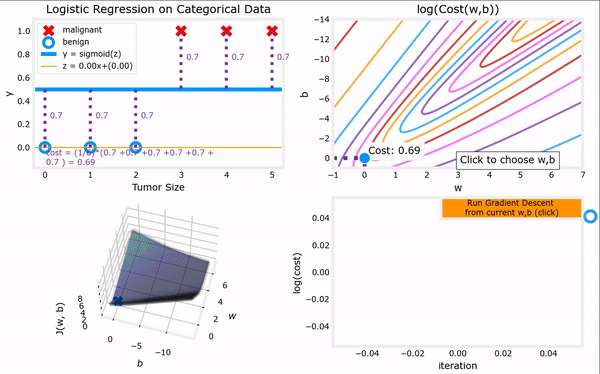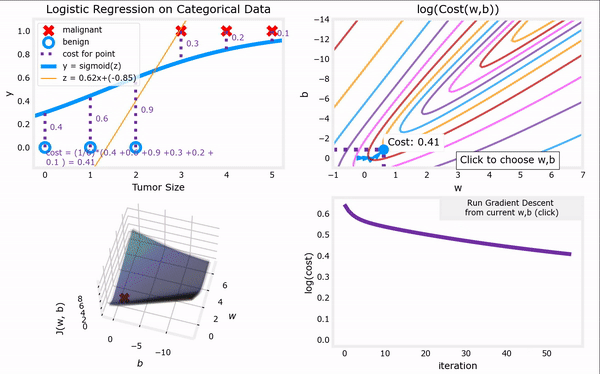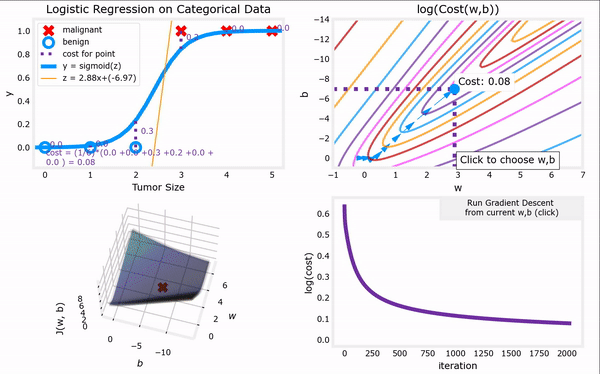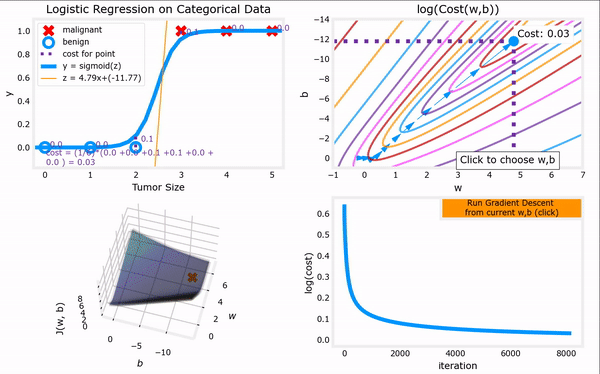
上图见课程资料:C1_W3_Lab06_Gradient_Descent_Soln
bug1:使用魔术命令%matplotlib widget,无法显示图,无法交互。
解决办法1:改成%matplotlib inline,可以将静态图显示出来,但是无法交互。
解决方法2:更新库conda update matplotlib。
当然,和“线性回归”类似,在“逻辑回归”中,也可以使用前面提到的概念来进一步优化梯度下降法:
- 使用“学习曲线”,监视梯度下降法的过程。
- 使用“向量化”加速代码运行效率。
- 使用“特征缩放”加速梯度下降法的收敛速度。
本节 Quiz:
- Which is the correct update step for?
√ The update steps look like the update steps for linear regression, but the definition of f w ⃗ , b ( x ( i ) ) f_{\vec{w},b}(x^{(i)}) fw,b(x(i)) is different.
× The update steps are identical to the update steps for linear regression.
4. 过拟合与正则化
现在已经学完“线性回归”和“逻辑回归”了,并且也介绍了“学习曲线”、“向量化”、“特征缩放”等一系列加速算法的方法。但是当梯度下降法迭代完成后,还有一类特殊的情况没有介绍,那就是“过拟合(overfitting)”和“欠拟合(underfitting)”。本节将介绍这两个概念,并介绍解决这类问题的方法——“正则化(regularization)”。
概念明晰:
- “Underfit”和“High bias”都表示欠拟合;“Overfit”和“High variance”都表示过拟合。
4.1 线性回归和逻辑回归中的过拟合
下面给出了“房价预测”、“肿瘤分类”两种问题中的“过拟合/欠拟合”情况:

- 欠拟合/高偏差:特征太少,甚至都不能很好的拟合训练集。“高偏差”有两层含义,一方面是拟合线和训练集的偏差很大;另一方面是因为我们先入为主的使用直线拟合,这本身与实际情况就是一种很大的偏差。
- just right:恰到好处!没有特别的术语描述这种情况。但即使对于一个全新的输入,也可以给出恰当的输出,于是称这样的模型具有很好的“泛化(generazilization)”特性。
- 过拟合/高方差:有太多的特征,可以完美的拟合数据集。但对于全新的输入,并不能给出恰当的输出。甚至训练集稍微变化一点点,都会拟合出完全不一样的曲线,也就是“高方差”。
注:“Underfit”和“High bias”都表示欠拟合;“Overfit”和“High variance”都表示过拟合。
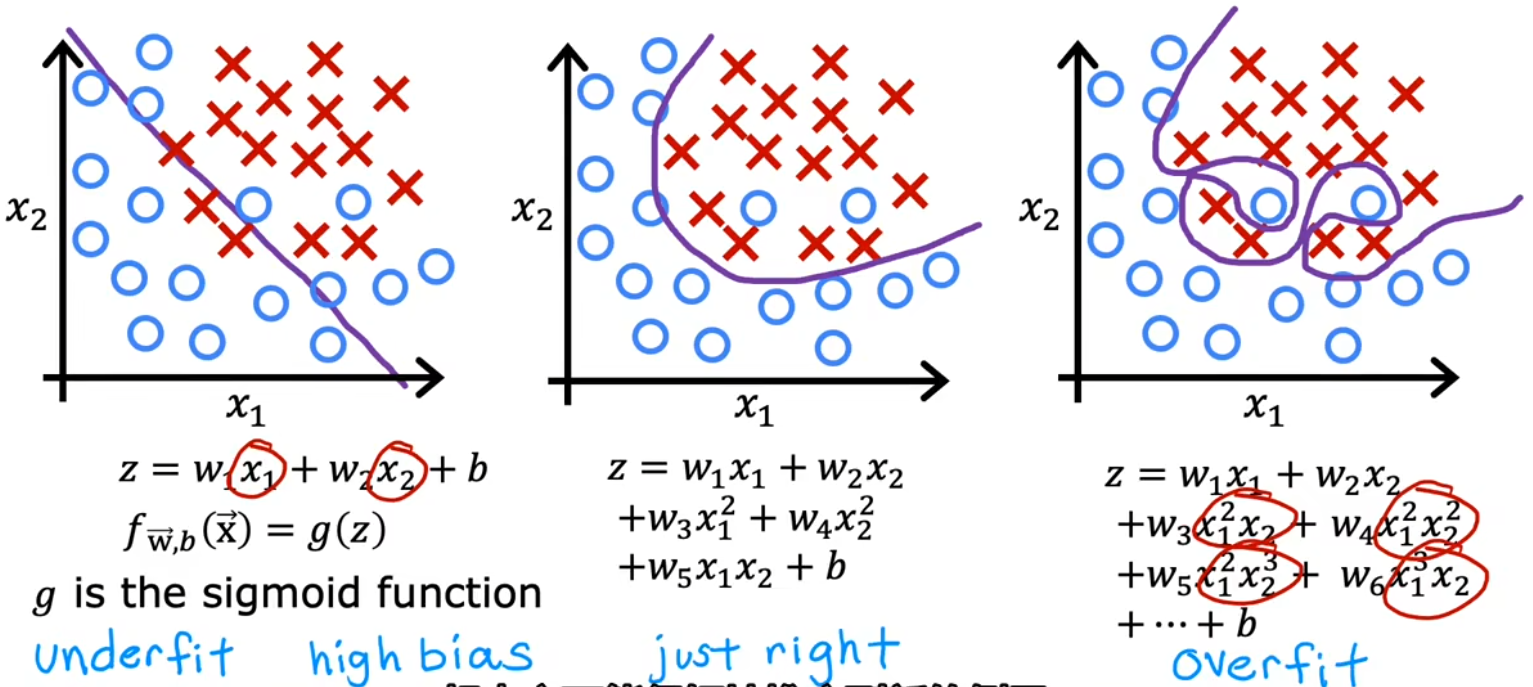
- 欠拟合/高偏差:决策边界是一条直线,看起来还行,但显然没有很好的学习到训练集。
- just right:决策边界是椭圆或椭圆的一部分,较好的拟合了数据,虽然并不是完美符合所有的训练数据。
- 过拟合/高方差:决策边界非常扭曲,以图完美符合所有的训练数据,但显然并不具有泛化特性。
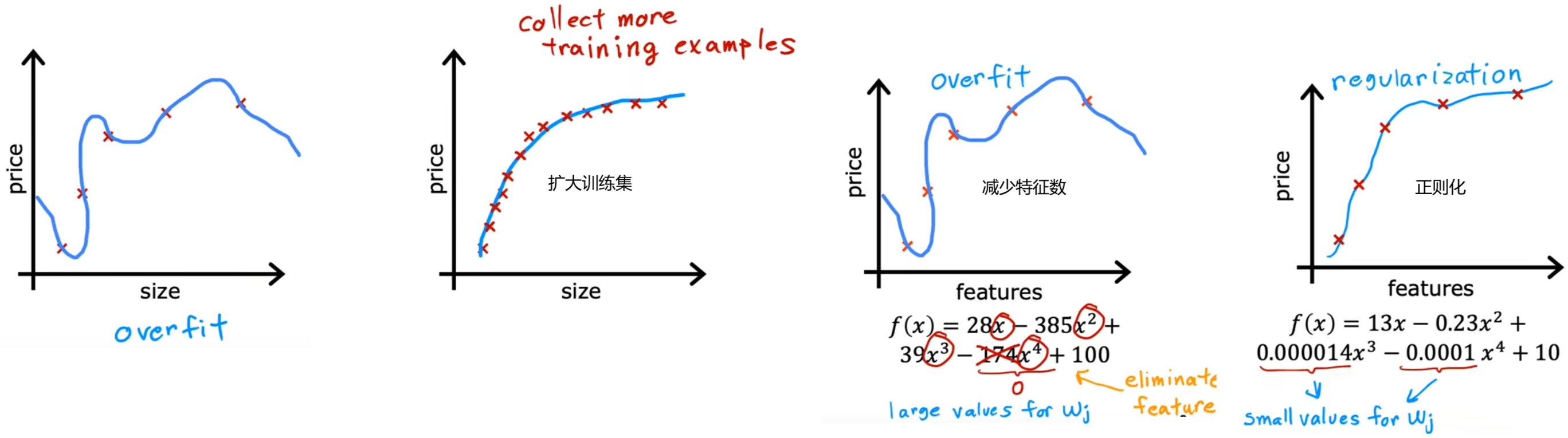
4.2 解决过拟合的三种方法
后续课程会介绍如何避免算法出错,并且介绍用于识别 欠拟合/过拟合 的工具,但现在先只介绍如何解决过拟合:
- 扩大训练集:此时即使有很多特征,相比于训练集很小时,其拟合曲线也会相对平滑。缺点是不一定能获取更多的训练数据。
- 减少特征数:也称为“特征选择”。“特征选择”除了靠直觉,在Course2中也会介绍一种自动选择特征的方法。缺点是有可能会丢弃有用特征。
- 正则化(regularization):保留所有的特征,但对于某个很大的特征 x j x_j xj,减小其参数 w j w_j wj(通常不会调整参数 b b b)。老师一直在用这个方法。
4.3 正则化
本节将具体介绍如何进行“正则化”。将会改进代价函数,来将其应用于“正则化”的本质就是改进代价函数,添加新的“正则项(regularization term)”,用于控制参数的大小:
Modified cost function:
J
(
w
⃗
,
b
)
=
1
m
∑
i
=
1
m
L
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
,
y
(
i
)
)
⏟
original cost
+
λ
2
m
∑
j
=
1
n
w
j
2
⏟
regularization term
+
λ
2
m
b
2
⏟
no use
,
λ
>
0.
\text{Modified cost function:} \quad J(\vec{w},b) = \underbrace{\frac{1}{m} \sum_{i=1}^{m}L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})}_{\text{original cost}} + \underbrace{\frac{\lambda}{2m}\sum_{j=1}^{n}w_j^2}_{\text{regularization term}} + \underbrace{\frac{\lambda}{2m}b^2}_{\text{no use}}, \; \lambda >0.
Modified cost function:J(w,b)=original cost
m1i=1∑mL(fw,b(x(i)),y(i))+regularization term
2mλj=1∑nwj2+no use
2mλb2,λ>0.
- λ \lambda λ:正则化参数(regularization parameter)。 λ = 0 \lambda=0 λ=0 时,没有正则化,此时模型会尽可能完美拟合数据(可能“过拟合”);随着 λ \lambda λ 增大,所有的 w j w_j wj 都会减小,拟合曲线会越平滑;但 λ \lambda λ 过大时,曲线会过于平滑,就会“欠拟合”。所以 λ \lambda λ 算是在平衡 “数据拟合” 和 “曲线平滑” 这两个目标。
- λ 2 m ∑ j = 1 n w j 2 \frac{\lambda}{2m}\sum_{j=1}^{n}w_j^2 2mλ∑j=1nwj2:正则项(regularization term)。分母中的 “ m m m” 是为了消除样本个数对于正则化效果的影响,而由于参数是平方项,分母中的 “ 2 2 2” 则是为了使代价函数偏导更加简洁。
- λ 2 m b 2 \frac{\lambda}{2m}b^2 2mλb2:有些工程师会在代价函数后加上对参数 b b b 的惩罚项,但实际上并不会有什么帮助。
可见“正则化”主要用于 解决“过拟合”,其作用是 使 所有 参数 同时 增大或减小,但不同参数的变化速度不同。相比于范围较小的特征,“正则化”对于范围较大的特征的参数影响更大,也就起到了调节曲线平滑程度的作用。
4.4 用于线性回归的正则方法
Linear regression model : f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b Linear cost function : min w ⃗ , b J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 + λ 2 m ∑ j = 1 n w j 2 Gradient descent repeat until convergence : { j = 1 , 2 , . . . , n . w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) , b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) . \begin{aligned} \text{Linear regression model} &: \quad f_{\vec{w},b}(\vec{x}) = \vec{w}·\vec{x} + b\\ \text{Linear cost function} &: \quad \min_{\vec{w},b} J(\vec{w},b) = \frac{1}{2m} \sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2 + \frac{\lambda}{2m}\sum_{j=1}^{n}w_j^2\\ \begin{aligned} \text{Gradient descent} \\ \text{repeat until convergence} \end{aligned} &: \left\{\begin{aligned} j &= 1,2,...,n. \\ w_j &= w_j - \alpha \frac{\partial }{\partial w_j} J(\vec{w},b) = w_j - \frac{\alpha}{m} \left( \sum_{i=1}^{m}[(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})·x^{(i)}_j] + \lambda w_j \right),\; \\ b &= b - \alpha \frac{\partial }{\partial b} J(\vec{w},b) = b - \frac{\alpha}{m} \sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)}).\\ \end{aligned}\right. \end{aligned} Linear regression modelLinear cost functionGradient descentrepeat until convergence:fw,b(x)=w⋅x+b:w,bminJ(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2+2mλj=1∑nwj2:⎩ ⎨ ⎧jwjb=1,2,...,n.=wj−α∂wj∂J(w,b)=wj−mα(i=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]+λwj),=b−α∂b∂J(w,b)=b−mαi=1∑m(fw,b(x(i))−y(i)).
下面来进一步分析参数的更新过程(同样也适用于“逻辑回归”中的正则方法):
w
j
=
w
j
−
α
m
(
∑
i
=
1
m
[
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
⋅
x
j
(
i
)
]
+
λ
w
j
)
=
(
1
−
α
λ
m
)
⏟
shrink
w
j
w
j
−
α
m
∑
i
=
1
m
[
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
⋅
x
j
(
i
)
]
⏟
usual update
\begin{aligned} w_j &= w_j - \frac{\alpha}{m} \left( \sum_{i=1}^{m}[(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})·x^{(i)}_j] + \lambda w_j \right)\\ &= \underbrace{(1-\alpha \frac{\lambda}{m})}_{\text{shrink} \; w_j}w_j - \underbrace{\frac{\alpha}{m}\sum_{i=1}^{m}[(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})·x^{(i)}_j]}_{\text{usual update}} \end{aligned}
wj=wj−mα(i=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]+λwj)=shrinkwj
(1−αmλ)wj−usual update
mαi=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]
- 第一项:添加正则化后,会在每次迭代过程中,都使参数 w j w_j wj 乘以一个略小于1的常数。
- 第二项:对于非正则化线性回归,正常的梯度下降法更新过程。
4.5 用于逻辑回归的正则方法
Logistic regression model : f w ⃗ , b ( x ⃗ ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) Logistic cost function : min w ⃗ , b J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] + λ 2 m ∑ j = 1 n w j 2 , Gradient descent repeat until convergence : { j = 1 , 2 , . . . , n . w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) , b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) . \begin{aligned} \text{Logistic regression model} &: \quad f_{\vec{w},b}(\vec{x}) = \frac{1}{1+e^{-(\vec{w}·\vec{x}+b)}}\\ \text{Logistic cost function} &: \quad \min_{\vec{w},b} J(\vec{w},b) = -\frac{1}{m} \sum_{i=1}^{m}[y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))] \\ & \qquad\qquad\qquad\qquad + \frac{\lambda}{2m}\sum_{j=1}^{n}w_j^2,\\ \begin{aligned} \text{Gradient descent} \\ \text{repeat until convergence} \end{aligned} &: \left\{\begin{aligned} j &= 1,2,...,n. \\ w_j &= w_j - \alpha \frac{\partial }{\partial w_j} J(\vec{w},b) = w_j - \frac{\alpha}{m} \left( \sum_{i=1}^{m}[(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})·x^{(i)}_j] + \lambda w_j \right), \\ b &= b - \alpha \frac{\partial }{\partial b} J(\vec{w},b) = b - \frac{\alpha}{m} \sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)}). \end{aligned}\right. \end{aligned} Logistic regression modelLogistic cost functionGradient descentrepeat until convergence:fw,b(x)=1+e−(w⋅x+b)1:w,bminJ(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]+2mλj=1∑nwj2,:⎩ ⎨ ⎧jwjb=1,2,...,n.=wj−α∂wj∂J(w,b)=wj−mα(i=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]+λwj),=b−α∂b∂J(w,b)=b−mαi=1∑m(fw,b(x(i))−y(i)).
本节Quiz:
Which of the following can address overfitting?
√ Collect more training data.
× Remove a random set of training examples.
√ Apply regularization.
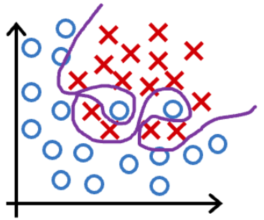
√ Select a subset of the more relevant features.You fit logistic regression with polynomial features to a dataset, and your model looks like this. What would you conclude? (Pick one)
× The model has high bias (underfit). Thus, adding data is likely to help.
√ The model has high variance (overfit). Thus, adding data is likely to help.
× The model has high bias (underfit). Thus, adding data is, by itself, unlikely to help much.
× The model has high variance (overfit). Thus, adding data is, by itself, unlikely to help much.
Suppose you have a regularized linear regression model. If you increase the regularization parameter λ \lambda λ, what do you expect to happen to the parameters w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn?
√ This will reduce the size of the parameters w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn.
× This will increase the size of the parameters w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn.注:C1_W3_Logistic_Regression包括了逻辑回归、正则化逻辑回归的练习题。










![[笔记]dubbo发送接收](https://img-blog.csdnimg.cn/direct/7ca575bb0d09448994416e144d5c6069.png)

