我的往期文章：
leetCode 647.回文子串 动态规划 + 优化空间 / 中心扩展法 + 双指针-CSDN博客
https://blog.csdn.net/weixin_41987016/article/details/133883091?spm=1001.2014.3001.5501leetCode 131.分割回文串 + 回溯算法 + 图解 + 笔记-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134700907?spm=1001.2014.3001.5501（一）利用动态规划来优化判断回文子串
- 利用动态规划高效地事先一次性计算出, 针对一个字符串
s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤.（来自代码随想录Carl老师的原话）原文链接：代码随想录 (programmercarl.com)
>>思路和分析
回文子串：讲究的是这个字符串里边左右两边是对称的，左右两边的元素是相同的。如果只判断这个字符串的最左面和最右面这两个元素相同的情况下，还知道中间的子串已经是回文的，那么就可以直接判断整个字符串它就是回文子串。
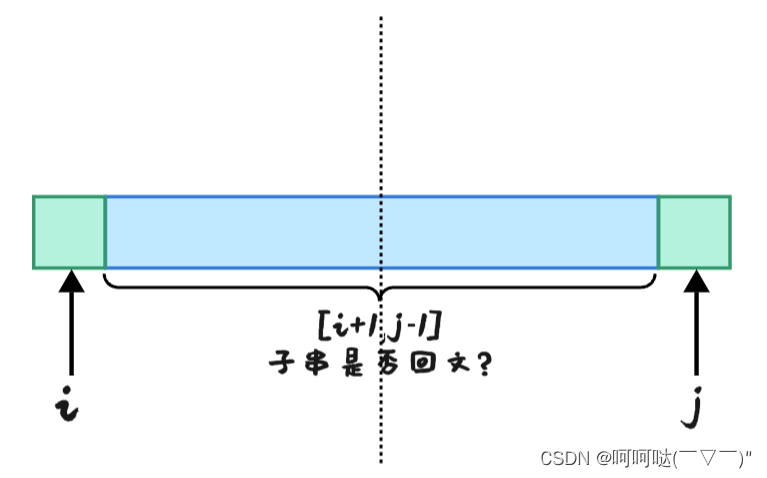
也就是说，如果在[i+1,j-1]范围的子串是一个回文串，再向两边拓展遍历的时候，那只需要判断两边这两个元素是否相同就可以了。若相同，dp[i][j]是回文串。
>>动规五部曲
1.确定dp数组以及下标的含义
- dp[i][j]:表示区间范围[i,j]的子串是否为回文子串。如果是，则dp[i][j] = true,否则为false
- 或者说，dp[i][j] 表示截取从 i 到 j 的子串是否为回文子串
2.确定递推式
if(j == i) dp[i][j]=true;
else if(j-i == 1) dp[i][j] = (s[i]==s[j]);
else dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]);3.dp 数组初始化
- dp[i][j]初始化为false
4.确定遍历顺序
一定要从下到上，从左到右遍历，这样能保证dp[i+1][j-1]是经过计算得来的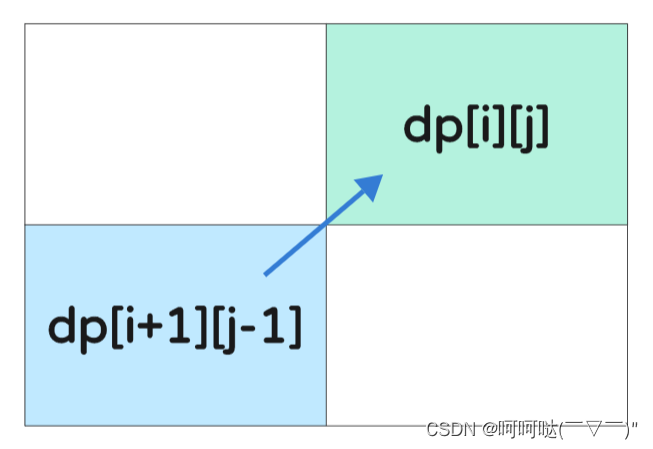
5.举例推导dp数组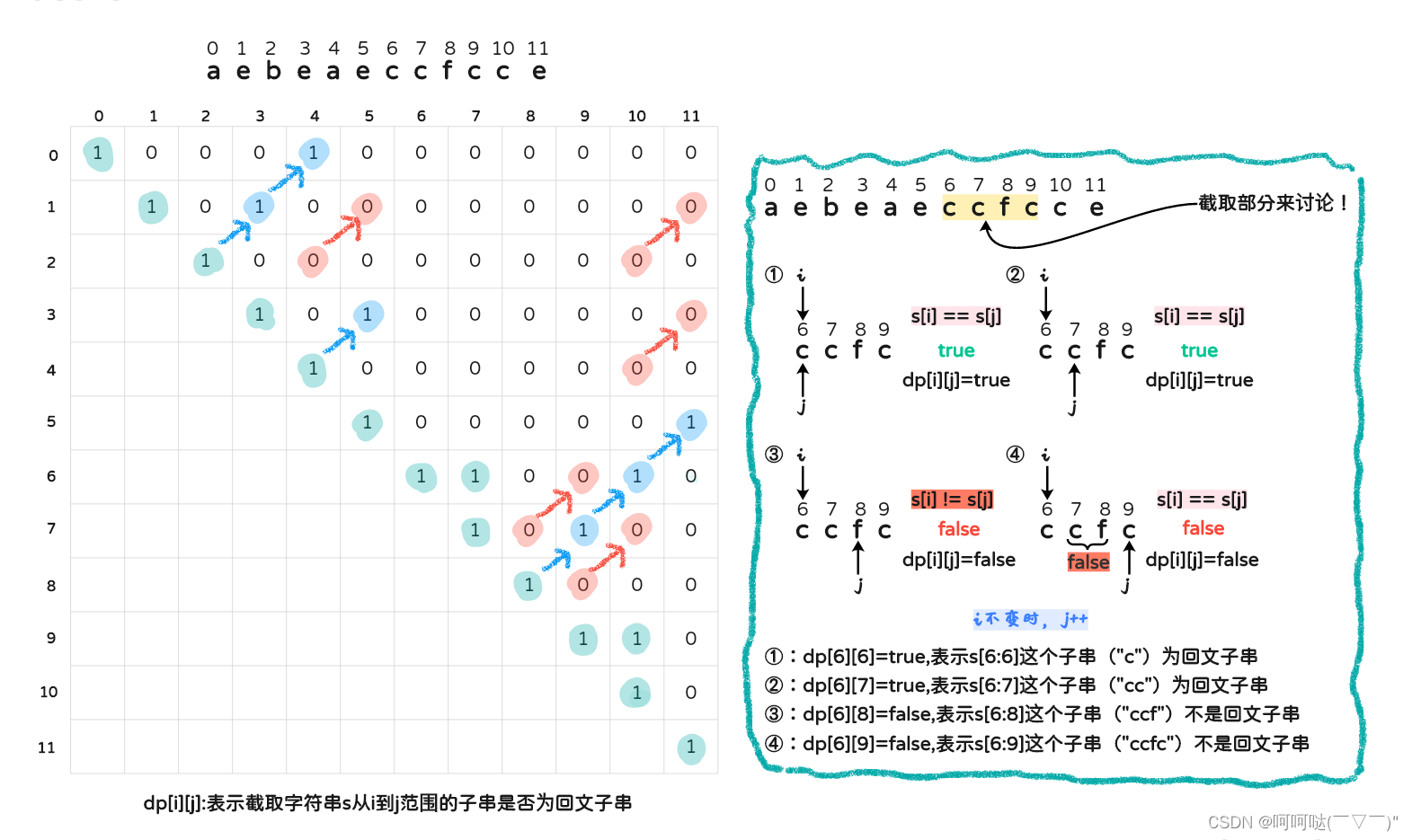
void computePalindrome(const string& s) {
// dp[i][j] 代表s[i:j]（双边包括）是否是回文子串
dp.resize(s.size(),vector<bool>(s.size(),false));// 根据字符串s，刷新布尔矩阵的大小
for(int i=s.size()-1;i>=0;i--) {
// 需要倒序计算，保证在i行时，i+1行已经计算好了
for(int j=i;j<s.size();j++) {
if(j == i) dp[i][j]=true;
else if(j-i == 1) dp[i][j] = (s[i]==s[j]);
else dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]);
}
}
}"aebeaeccfcce"
1 0 0 0 1 0 0 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 1 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 1
0 0 0 0 0 0 1 1 0 0 1 0
0 0 0 0 0 0 0 1 0 1 0 0
0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 1
"acgcabbfcc"
1 0 0 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0 1 （二）分割回文串 + 动态规划 + 回溯算法 + 优化
class Solution {
public:
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
vector<vector<bool>> dp; // 放事先计算好的是否回文子串的结果
void backtracking(const string& s,int startIndex) {
// 如果起始位置已经大于 s 的大小，说明已经找到了一组分割方案了
if(startIndex >= s.size()) {
result.push_back(path);
return;
}
for(int i=startIndex;i<s.size();i++) {
if(dp[startIndex][i]) { // 是回文子串
// 获取[startIndex,i] 在 s 中的子串
string subStr = s.substr(startIndex,i-startIndex+1);
path.push_back(subStr);
}else continue; // 不是回文，跳过
backtracking(s,i+1);// 寻找 i+1 为起始位置的子串
path.pop_back();// 回溯过程，弹出本次已经添加的子串
}
}
void computePalindrome(const string& s) {
// dp[i][j] 代表s[i:j]（双边包括）是否是回文子串
dp.resize(s.size(),vector<bool>(s.size(),false));// 根据字符串s，刷新布尔矩阵的大小
for(int i=s.size()-1;i>=0;i--) {
// 需要倒序计算，保证在i行时，i+1行已经计算好了
for(int j=i;j<s.size();j++) {
if(j == i) dp[i][j]=true;
else if(j-i == 1) dp[i][j] = (s[i]==s[j]);
else dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]);
}
}
}
vector<vector<string>> partition(string s) {
computePalindrome(s);
backtracking(s, 0);
return result;
}
};参考和推荐文章：
代码随想录 (programmercarl.com)https://www.programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html#%E6%80%9D%E8%B7%AF
摘选代码随想录的总结：
- 总结难点：
- 如何切割？切割问题可以抽象为组合问题
- 如何模拟那些切割线？
- 切割问题中递归如何终止？
- 在递归循环中如何截取子串？
- 如何判断回文？
递归用于纵向遍历，for循环用于横向遍历当切割线迭代至字符串末尾，说明找到一种方法。类似组合问题，为了不重复切割同一位置，利用 start_index 作为标记，记录下一轮。递归的起始位置（切割线）。切割过的地方不能重复切割，故递归函数传入 i+1
![[笔记]dubbo发送接收](https://img-blog.csdnimg.cn/direct/7ca575bb0d09448994416e144d5c6069.png)
