class Solution {
public:
int search(vector<int>& nums, int target) {
int l=0;
int r=nums.size()-1;
while(l<=r){
int mid=(l+r)>>1;
if(target==nums[mid]) return mid;
if(target>nums[mid]){
l=mid+1;
}
else{
r=mid-1;
}
}
return -1;
}
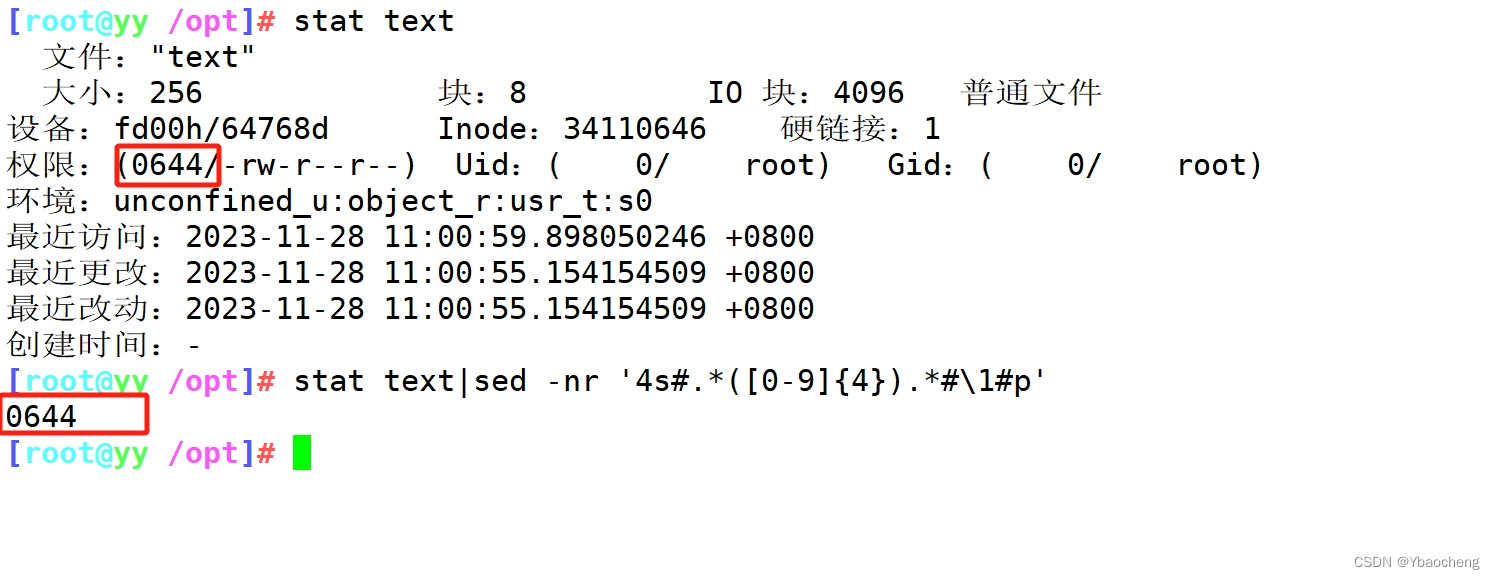
};之前就已经熟悉二分法了,有两次wa,第一次是因为一开始的右边界取了一个数为数组的长度值int r=nums.size(),终止条件是l<=r,导致数组可能越界(针对于数组为[-1],target为5的情况),r能取到的时候要注意取值;第二次wa是终止条件写成了l<r,且int r=nums.size()-1,会出现有右端点永远取不到的情况,一直取左端点,改成l<=r,最后ac。
看完题解发现:
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。重点是区间定义。
时间复杂度是o(logn)的,而空间复杂度是o(1)的。
如果l和r是左闭,右开
// 版本二
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int l=0;
if(nums.size()==0) return 0;
int r=nums.size()-1;
while(l<=r){
while(l<=r&&nums[l]!=val){
l++;
}
while(l<=r&&nums[r]==val ){
r--;
}
// if(l==r){
// return l+1;
// }
if(l>r) return l;
swap(nums[l],nums[r]);
}
return l+1;
}
};这道题之前看过,所以也是挺快ac,有一次wa是因为没考虑数组为空的情况,要注意特判。是双指针法。
暴力解法是对每一个元素,判断是或不是,是的话删除移动元素。
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
if(nums.size()==0) return 0;
int res=0;
for(int i=0;i<nums.size();){
while(i<nums.size()&&nums[i]!=val){
i++;
res++;
}
int tmp=i;
while(tmp<nums.size()&&nums[tmp]==val){
tmp++;
}
if(tmp==nums.size()) return res;
int cha=tmp-i;
for(int j=i;j<nums.size()-cha;j++){
// nums[j]=nums[j+cha];
swap(nums[j],nums[j+cha]);
}
i++;
res++;
}
return res;
}
};我第一次wa的原因是直接将后面的元素移到了前面,但是仍然可能遍历到后面,被统计,但其实该元素已经移到前面了,所以要swap。
暴力解法空间复杂度也是O(1),时间复杂度是O(n的平方)
我的是改变了相对位置的写法,以下是copy的没更改相对位置的写法。
// 时间复杂度:O(n)
// 空间复杂度:O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if (val != nums[fastIndex]) {
nums[slowIndex++] = nums[fastIndex];
}
}
return slowIndex;
}
};今日收获:一个半小时的代码编写;要注意边界条件。

![[笔记]dubbo发送接收](https://img-blog.csdnimg.cn/direct/7ca575bb0d09448994416e144d5c6069.png)