树的概念
1.树的定义:树是n(n>=0)个结点的有限集合
当n==0时,称为”空树“
当n>=0时,有且仅有一个称为”根“的特定结点,该结点没有前驱,但是却有一个或者多个后继结点。
除了根节点以外的n-1个结点可划分为多个有限集Ti(i = 1,2,3,4.....),每个Ti都是一个树,称为”根的子树“,每颗子树只有一个前驱结点,有一个或者多个后继结点。
树的基本术语
1.结点:包含一个数据元素以及若干指向其子树的分支。
结点的度:结点拥有子树的个数 树的度:树中所有结点的度的最大值。
叶子结点:度为0的结点 内部结点:除了根结点以及叶子结点,其余剩余的结点

子孙结点:该结点的子树的所有结点。
结点的层次:根结点在第一层,K在第四层。
树的深度:树的所有层次中最大值变为深度。
二叉树
二叉树的定义:一个根节点及两颗互不相交的,被称为”左子树“和”右子树“二叉树。
1.每个结点的度不大于2
2.每个结点只能有0,1,2个孩子,左孩子叫左子树,右孩子叫右子树
3.二叉树的五种形态

二叉树的性质
性质1:在二叉树的第i层,层上至多有2^(i-1)个结点
性质2:深度为k的二叉树至多有2^k-1个结点
性质3:对于任意的一个二叉树T,若终端的节点数为n0,度为2的结点数n2,则no = n2+1
性质4:具有n个结点的完全二叉树的深度为|log2n|+1【高斯函数,取不大于该数值的整数】
性质5:对于具有n个结点的完全二叉树,如果完全按照对满二叉树结点进行连续编号的方式,从1开始进行序号编写
一,当i=1时,则结点为根节点,无双亲结点,若i>1,则双亲结点的序号为i/2
二,若2i<=n,则结点i的左孩子结点序号为2i,否则无左孩子结点
三,若2i+1>=n,则结点i的右孩子结点序号为2i+1,否则无右孩子结点
概念强调:
满二叉树,就是从1到k-1层的结点的度都为2,满二叉树是同样深度叶子结点最多的,也是结点最多的
完全二叉树:结点数n(n<=2^k-1),从1到n的结点结点一一满足对应关系(即都是和满二叉树完全对应)【满二叉树从最后一个结点连续的去掉任意个结点则为完全二叉树】
二叉树的顺序存储
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define maxsize 51 //第一位存放二叉树结点个数,从而根结点序号为1,所有节点序号皆满足二叉树性质
#define elemtype char
typedef char SqBiTree[maxsize];
void InitTree(SqBiTree T)
{
char j;
int i;
printf("请输入二叉树结点个数:");
scanf("%c",&j);
T[0]=j;
printf("结点个数为%c\n",j);
for(i=1;i<maxsize;i++)
{
T[i]='\0';
}
}
void CreateTree(SqBiTree T,int i) //递归建立顺序二叉树
{
fflush(stdin);
elemtype x;
scanf("%c",&x);
if(x=='#')
{
T[i]='\0';
return;
}
T[i]=x;
printf("请输入其左子结点数据:");
CreateTree(T,2*i);
printf("请输入其右子结点数据:");
CreateTree(T,2*i+1);
}
void PrintTree(SqBiTree T)
{
int i;
for(i=0;i<maxsize;i++)
{
printf("%c",T[i]);
}
}
void main()
{
SqBiTree t;
InitTree(t);
printf("请输入根节点数据:");
CreateTree(t,1);
PrintTree(t);
}二叉树的链式存储结构
1.结构体定义的初始化
//结构体初始化
typedef struct BinaryTreeNode;
{
struct BinaryTreeNode *left;
struct BinaryTreeNode *right;
char data;
}BTNode;2.创建一个二叉树
动态内存分配结点空间
//创建二叉树
BTNode* CreateTreeNode(BTDataType x)
{
BTNode *Node = (BTNode*)malloc(sizeof(BTNode));
Node->data = x;
Node->left = NULL;
Node->right = NULL;
return Node;
} 3.前序遍历
//前序遍历
void PreNode(BTNode *root)
{
if(root == NULL)
{
printf("NULL");
return;
}
printf("%c",root->data);
PreNode(root->left);
PreNode(root->right);
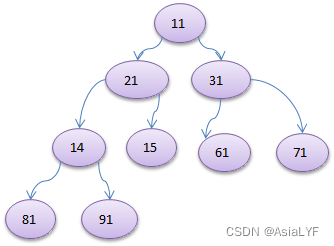
} 图解(图来自于B站up主@青岛大学-王卓老师):

4.中序遍历
//中序遍历
void MidNode(BTNode *root)
{
if(root == NULL)
{
printf("NULL");
return;
}
MidNode(root->left);
printf("%c",root->data);
MidNode(root->right);
}图解(图来自于B站up主@青岛大学-王卓老师):

5.后序遍历
//后序遍历
void LastNode(BTNode *root)
{
if(root == NULL)
{
printf("NULL");
return;
}
PreNode(root->left);
PreNode(root->right);
printf("%c",root->data);
}图解(图来自于B站up主@青岛大学-王卓老师):

6.层序遍历
原理:每一层每一层的进行遍历,当结点出队列的同时,判断当前的结点是否有左右孩子,如果有,则将其送入队列,以此类推,知道队列为空。
void LevelTraverse(BiTree T){
if(T != NULL)//T不是#就执行
{
queue<BiTree> q;//新建队列q 队内元素的类型是BiTree
q.push(T);//T入队
while(!q.empty())//队列不为空时就执行
{
BiNode* node = q.front();//取队列首个元素并赋值给node
cout << node -> data;//输出node的值
q.pop();//剔除队列首个元素
if(node -> lchild != NULL)
q.push(node -> lchild);//如果node的左子不为空将左子入队
if(node -> rchild != NULL)
q.push(node -> rchild);//如果node的右子不为空将右子入队
}
}
}
7.二叉树的查找:逐个结点找,找到对应需要的数据
int find(int data,Node X)
{
if(X == NULL)
return 0;
if(X.data == data)
return 1;
int flag1 = false;
int flag2 = false;
flag1 = find(X.left,data);
flag2 = find(X.right,data);
return flag2||flag1;
}8.二叉树的深度
如果是空树,递归计算左子树的深度为m,递归计算右子树深度为n,二叉树的深度为m与n的深度较大值加1。
int depth(BiTree T)
{
if(T == NULL)
return 0;
else
{
m = depth(T->lchild);
n = depth(T->rchild);
if(m>n)
return (m+1);
else
return (n+1);
}
}9.二叉树的结点计算
左子树结点的个数+右子树结点的个数+1
int NodeCount(BiTree T)
{
if(T == NULL)
{
return 0;
}
else
return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}