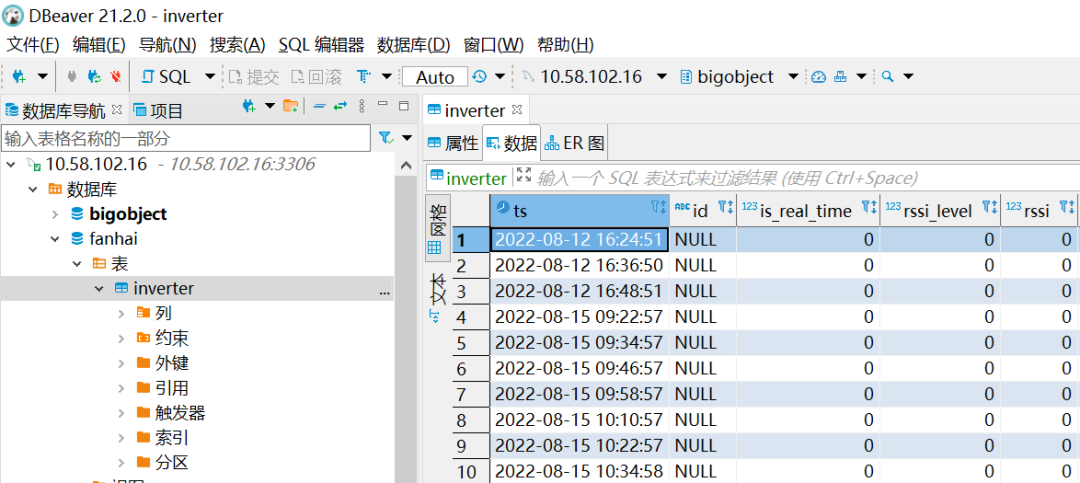
题目

已知两颗二叉树，将它们合并成一颗二叉树。合并规则是：都存在的结点，就将结点值加起来，否则空的位置就由另一个树的结点来代替。例如：
两颗二叉树是:
Tree 1

Tree 2

合并后的树为

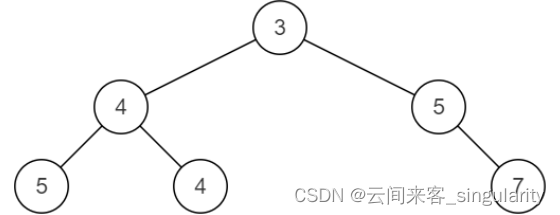
数据范围：树上节点数量满足0≤n≤500，树上节点的值一定在32位整型范围内。

进阶：空间复杂度 O(1)，时间复杂度 O(n)

示例1

输入：{1,3,2,5},{2,1,3,#,4,#,7}

返回值：{3,4,5,5,4,#,7}

示例2

输入：{1},{}

返回值：{1}

---

思路1：递归

• step 1：首先判断t1与t2是否为空，若为空则用另一个代替，若都为空，返回的值也是空。
• step 2：然后依据前序遍历的特点，优先访问根节点，将两个根点的值相加创建到新树中。
• step 3：两棵树再依次同步进入左子树和右子树。

---

代码1

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */

public class Solution {
    /**
     * 
     * @param t1 TreeNode类 
     * @param t2 TreeNode类 
     * @return TreeNode类
     */
    public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
        if(t1 == null) {
            return t2;
        }
        if(t2 == null) {
            return t1;
        }
        TreeNode head = new TreeNode(t1.val + t2.val);
        head.left = mergeTrees(t1.left, t2.left);
        head.right = mergeTrees(t1.right, t2.right);
        return head;
    }
}

---

思路2：非递归层次遍历

非递归的层次遍历，也可以实现两棵树同步遍历节点相加，重点是两棵树从根节点开始每个节点是同步走的，因此可以使用队列辅助两个二叉树分别同时层次遍历。

具体做法：

• step 1：首先判断t1与t2是否为空，若为空则用另一个代替，若都为空，返回的值也是空。
• step 2：使用三个辅助队列，第一个队列q用于暂存合并后的二叉树的层次遍历节点，第二个队列q1用于暂存t1的层次遍历节点，第三个队列q2用于暂存t2的层次遍历节点。
• step 3：两棵树同步层次遍历，先将根节点加入队列中，同时根节点优先合并。
• step 4：每次从队列分别弹出一个元素，判断分别二者的左右子节点是否存在，若是都存在，则相加合并，若是只存在一个则连接该存在的节点，若是都不存在则连接null。

---

代码2

import java.util.*;

public class Solution {
    public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
        //若只有一个节点返回另一个，两个都为null自然返回null
        if(t1 == null) {
            return t2;
        }
        if(t2 == null) {
            return t1;
        }

        //合并根节点
        TreeNode head = new TreeNode(t1.val + t2.val); 
        //连接后的树的层次遍历节点
        Queue<TreeNode> q = new LinkedList<TreeNode>(); 
        //分别存两棵树的层次遍历节点
        Queue<TreeNode> q1 = new LinkedList<TreeNode>(); 
        Queue<TreeNode> q2 = new LinkedList<TreeNode>();
        q.offer(head);
        q1.offer(t1);  
        q2.offer(t2);

        while (!q1.isEmpty() && !q2.isEmpty()) {
            TreeNode node = q.poll();
            TreeNode node1 = q1.poll(); 
            TreeNode node2 = q2.poll();
            TreeNode left1 = node1.left;
            TreeNode left2 = node2.left;
            TreeNode right1 = node1.right;
            TreeNode right2 = node2.right;

            if(left1 != null || left2 != null) { 
                //两个左节点都存在
                if(left1 != null && left2 != null) { 
                    TreeNode left = new TreeNode(left1.val + left2.val);
                    node.left = left; 
                    //新节点入队列
                    q.offer(left);  
                    q1.offer(left1);
                    q2.offer(left2);
                //只连接一个节点
                } else if(left1 != null) {
                    node.left = left1;
                } else {
                    node.left = left2;
                }
            }

            if(right1 != null || right2 != null) {
                //两个右节点都存在
                if(right1 != null && right2 != null) { 
                    TreeNode right = new TreeNode(right1.val + right2.val);
                    node.right = right;
                    //新节点入队列
                    q.offer(right); 
                    q1.offer(right1);
                    q2.offer(right2);
                //只连接一个节点
                } else if(right1 != null) {
                    node.right = right1;
                } else {
                    node.right = right2;
                }
            }
        }
        return head;
    }
}