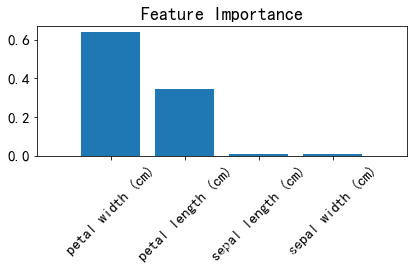
有 N 堆石子,每堆的石子数量分别为 a1,a2,…,aN。
你可以对石子堆进行合并操作,将两个相邻的石子堆合并为一个石子堆,例如,如果 a=[1,2,3,4,5],合并第 2,3 堆石子,则石子堆集合变为 a=[1,5,4,5]。
我们希望通过尽可能少的操作,使得石子堆集合中的每堆石子的数量都相同。
请你输出所需的最少操作次数。
本题一定有解,因为可以将所有石子堆合并为一堆。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含整数 N。
第二行包含 N 个整数 a1,a2,…,aN。
输出格式
每组数据输出一行结果。
数据范围
1≤T≤10,
1≤N≤105,
0≤ai≤106,
∑ai≤106,
每个输入所有 N 之和不超过 105。
自己的解法:
- 用堆排序的方法,对于每一组数据,建立初始小根堆,进行堆排序。
- 每次排好一个元素后,进行对已排序序列检查,如果已经完成堆排序的序列的部分和(从前往后)可以大于等于目前的最大值,则合并这部分。(全是0的情况除外)
- 合并后更新下次排序需要的参数,继续进行堆排序,合并。
- 直至所有的数都一样或者合成一堆,算法停止,输出答案,进行下一组的堆排序。
- 这需要每次合并后都检查是否每个数都一样。
- 因为考虑到数据量的问题,用枚举是O(n2)的复杂度,会超时,用堆排序降到O(nlog2n)的复杂度。
我的推导过程:

但是考虑到如果每次排序后都进行检查,那么时间复杂度也会上升到O(n2)
自己的代码(没写完):
#include<iostream>
#include<vector>
using namespace std;
vector<vector<int> > v; //v存放所有的数组
int max_vj = -0xffff; //每组数据的最大值
int res = 0;
//小根堆的建立
void HeapAdjust(vector<int> &A, int k, int len){
int t = A[k]; //暂存这个分支结点
for(int i = 2*k; i <= len; i *= 2){ //从这个分支结点开始向下调整
if(i < len && A[i] > A[i+1]) i++; //右孩子更小
if(t <= A[i]) break; //分支结点已是子堆中的最小值,符合特性
else{ //不符合特性,需要调整
A[k] = A[i]; //换的时候只是覆盖
k = i; //下标要交换,下次还说与A[0]比较
}
}
A[k] = t; //放到最终符合特性的位置上
}
void BuildMinHeap(vector<int> &A, int len){
//从最后一个分支结点开始,逐级向上建堆
for(int i = len/2; i > 0; i--)
HeapAdjust(A, i, len);
}
//堆排序
void HeapSort(vector<int> &A, int len){
for(int i = len; i > 1; i--){ //n-1趟交换和建堆过程
swap(A[i], A[1]); //堆顶元素和堆底元素互换
//交换后检查是否符合合并的条件
//如果已经完成堆排序的序列的部分和(从后往前)可以大于等于目前的最大值,则合并这部分
//合并后更新下一次需要的参数
if(){
A[len-1] = A[len]+A[len-1]; //合并
if(A[len-1] > max_vj) max_vj = A[len-1]; //更新最大值、长度、合并次数
A[0]--; len--; res++;
}
HeapAdjust(A, 1, i-1); //将剩余的元素调整
}
}
int main(){
int T, N, an; //T组测试数据,每组数据包含N个整数an
cin >> T; //测试数据的数量
vector<int> vj; //每组数据存放的数组
//下面搞定输入
for(int i = 0; i < T; i++){
cin >> N; //N个整数
vj.clear(); //对数组先清空
vj.push_back(N); //每个数组的第一个位置存放这个数组的长度
for(int j = 0; j < N; j++){
cin >> an; //输入a1~an
vj.push_back(an);
}
v.push_back(vj);//将每组数据放入v
}
for(int i = 0; i < T; i++){
vector<int> vj = v[i];
if(vj[0] == 2 && vj[1] != vj[2]){ //如果只有两个数且不相等
cout << 1 << endl;
continue;
}else if(vj[0] == 1){ //如果只有一个数
cout << 0 << endl;
continue;
}
//找出每组数据的最大值
for(int j = 1; j <= vj[0]; j++)
if(vj[j] > max_vj) max_vj = vj[j];
//对于每组数据建立初始的小根堆
BuildMinHeap(vj, vj[0]); //建堆
HeapSort(vj, vj[0]); //堆排序的同时合并
cout << res << endl;
max_vj = -0xffff; //重置
res = 0;
//测试堆排序结果
// for(int i = 1; i <= vj[0]; i++) cout << vj[i] << " ";
// cout << endl;
// cout << max_vj << endl;
}
return 0;
}
y总的方法:
他的方法是用的数论的推导
总的石子个数sum,最终每堆石子cnt个,cnt只有整除sum才可以
cnt的数量等于sum的约数个数,平均每个数的约数个数是O(logn)个
106以内,约数个数最多的数是720720,有240个约数
int范围内,约数个数最多的数有1600个
- 知道了这个前提,我们就可以用枚举的方法,枚举所有的约数,找到可以取到的并整除sum的数
- 在所有的数里面找到合并次数最少的方案
- 我们知道,最终合并后有sum/cnt堆石子,原来有n堆
- 所以合并的次数为 n-sum/cnt
- 我们只需要找到一个最小的符合条件的cnt
- 所以我们只需要从小到大枚举cnt,看是否成立就可以了
一开始还有一个条件我没注意到,只能合并相邻的两堆,这样堆排序好像没法用了
那我们如何判断cnt是否成立?(能否将每一堆的数量变成cnt)
- 对于每个cnt,我们对原始序列从前向后枚举
- 如果当前堆的石子数量大于cnt,那一定无解,枚举下一个cnt
- 如果当前堆的石子数量等于cnt,如果后面的数量是0,可以加到前面或后面的一堆;如果不是0,那就合并到下一段
- 根据计算,大约240个约数,最多用107次计算量,可以在规定的时间内完成
最后附一下代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int w[N];
//判断当前的约数是否符合条件
bool check(int cnt)
{
//从前向后枚举序列的每一段
for (int i = 0, s = 0; i < n; i ++ )
{
s += w[i]; //合并相邻的两段
if (s > cnt) return false; //如果合并后的石子数量大于cnt,无解
if (s == cnt) s = 0; //如果等于这个约数cnt,继续合并后面的段
}
return true;
}
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d", &n); //石子的堆数
int sum = 0; //石子的总数sum
for (int i = 0; i < n; i ++ ) //输入每堆石子个数
{
scanf("%d", &w[i]);
sum += w[i]; //计入到总数sum
}
for (int i = n; i; i -- ) //对于每堆石子,枚举寻找符合条件的cnt
if (sum % i == 0 && check(sum / i))//如果cnt能够整除sum,并且操作次数最小,且有解
{
printf("%d\n", n - i); //输出答案
break;
}
}
return 0;
}
//作者:yxc
//链接:https://www.acwing.com/activity/content/code/content/5027948/
//来源:AcWing
//著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。