文章目录
- 背景
- IOU:Intersection Over Union
- precision(精度)和recall(召回率)
- TP、TN 、FP 、FN
- AP和mAP
- 首先回顾两个概念
- PR曲线
- AP(Average Precision)
- mAP(mean Average Precision)
背景
目标检测的任务是找出图像中所有感兴趣的目标(物体),确定它们的位置和大小,是计算机视觉领域的核心问题之一。以下图为例,图中需要识别3类物体:car(车)、bicycle(自行车)、dog(狗),通过特定的目标检测算法希望最终把每类物体检测出来,每类物体用一个矩形框框出来并且输出对应的类别。
因此,目标检测可以简单的理解为用个框把物体框出来并告诉我这个框里是什么。

IOU:Intersection Over Union
- 并集里面的交集,公式如下
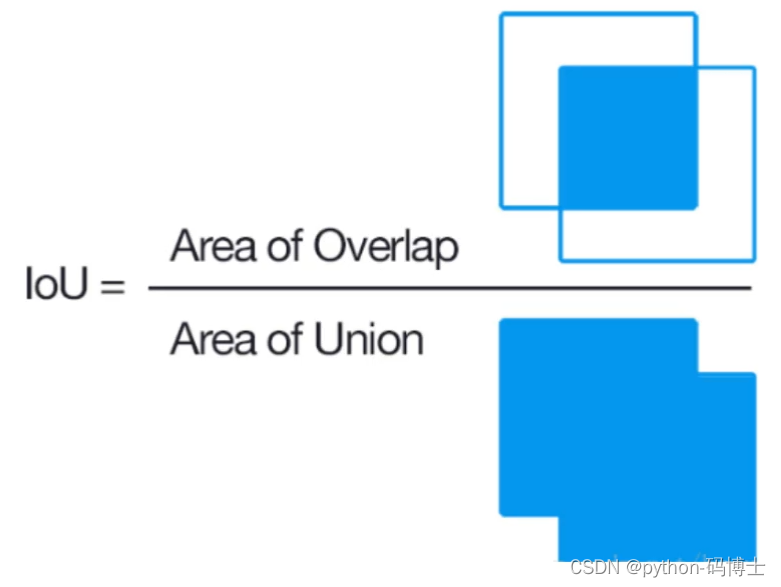

对应的数学公式如下:
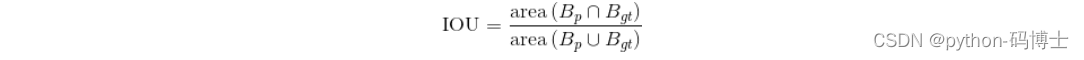
precision(精度)和recall(召回率)

所谓精度,也就是我们得到的预测框到底有多少面积是在真值框里面的,这个重叠面积除以检测框面积就是精度。形象化理解可以理解成“命中率”,即我预测的有多少在真值框里面。
召回率从字面意思比较好理解,就是我发出去多少最终收回来多少,即正确的预测框数量除以所有正确框的数量。
从上述概念上可以看出,精度和召回率是一般是反的。精度高了,召回率一般会低;召回率高了,精度一般会低。想象一下,如果我们需要提出一种目标检测算法来检测图像中的狗,为了尽可能的提高召回率,我们可以检出处很多很多框以尽可能的来包含图片中可能出现狗的地方,甚至可以直接以整幅图像为预测框,这时候召回率是最高的接近于1,但是很明显,精度很低。
尽管理解了精度和召回率的概念,但是实际计算时还需要借助额外的几个指标参数,通过这几个额外的指标参数可以使得我们更容易计算精度和召回率。
TP、TN 、FP 、FN
在一个数据集检测中,会产生四类检测结果:
True Positive(TP)、False Positive (FP)、False Negative (FN)、True Negative (TN):
T ——true 表示正确
F——false 表示错误
P—— positive 表示积极的,看成正例
N——negative 表示消极的,看成负例
后面为预测结果,前面是预测结果的正确性。如:
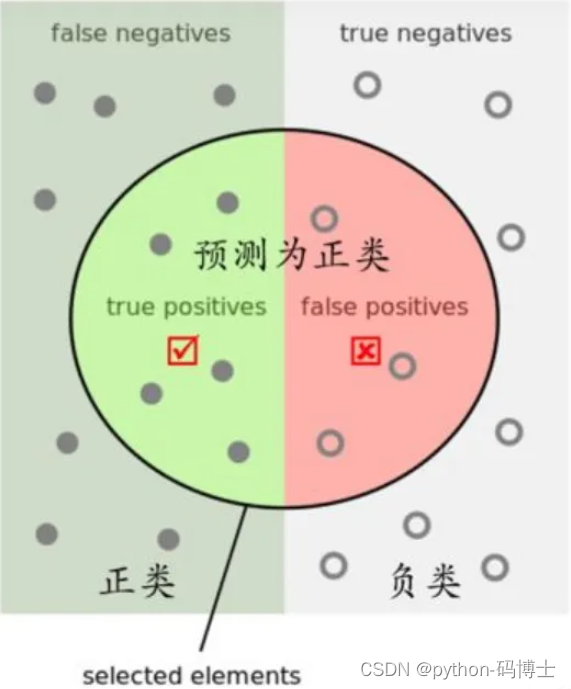
T P—— 预测为 P (正例), 预测对了, 本来是正样本,检测为正样本(真阳性)。
T N—— 预测为 N (负例), 预测对了, 本来是负样本,检测为负样本(真阴性)。
F P—— 预测为 P (正例), 预测错了, 本来是负样本,检测为正样本(假阳性)。
F N—— 预测为 N (负例), 预测错了, 本来是正样本,检测为负样本(假阴性)。
PS:实际目标检测中我们不会去检测背景(因为我们不会去为背景画个框),因此一般不会去计算TN这个值。
知识问答:
已知一张图中有100个细胞,其中正常细胞80个,癌细胞20个。
目标:找出所有癌细胞
结果:找出了50个细胞,其中20个是癌细胞,30个是正常细胞。
答案:TP=20 TN=50 FP=30 FN=0
看这里更容易理解这一块内容:https://blog.csdn.net/W1995S/article/details/114988637
TP+FP+TN+FN:样本总数。
TP+FN:实际正样本数。
TP+FP:预测结果为正样本的总数,包括预测正确的和错误的。
FP+TN:实际负样本数。
TN+FN:预测结果为负样本的总数,包括预测正确的和错误的
四种情形组成的混淆矩阵如下:

还有一个指标:
准确率(Accuracy): 模型判断正确的数据(TP+TN)占总数据的比例
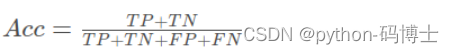
直观上说,我们用上述标准来衡量目标检测的好坏似乎已经够了。然而,目标检测问题中的模型的分类和定位都需要进行评估,每个图像都可能具有不同类别的不同目标,因此,在图像分类问题中所使用的标准度量不能直接应用于目标检测问题。
缺点:准确率是分类问题中最简单也是最直观的评价指标,但存在明显的缺陷。比如,当负样本占99%时,分类器把所有样本都预测为负样本也可以获得99%的准确率。所以,当不同类别的样本比例非常不均衡时,占比大的类别往往成为影响准确率的最主要因素。
AP和mAP
首先回顾两个概念
IOU:预测框与真实框的重叠程度,也叫IOU阈值,大于IOU阈值的预测框是存在的,小于IOU阈值的候选框是不存在的。
置信度:用来判断边界框内的物体是正样本还是负样本,大于置信度阈值的判定为正样本,小于置信度阈值的判定为负样本即背景。
PR曲线
我们当然希望检测的结果P越高越好,R也越高越好,但事实上这两者在某些情况下是矛盾的。比如极端情况下,我们只检测出了一个结果,且是准确的,那么Precision就是100%,但是Recall就很低;而如果我们把所有结果都返回,那么必然Recall必然很大,但是Precision很低。
因此在不同的场合中需要自己判断希望P比较高还是R比较高。如果是做实验研究,可以绘制Precision-Recall曲线来帮助分析。
这里我们举一个简单的例子,假设我们的数据集中共有五个待检测的物体,以其中一个物体为例,我们的模型给出了10个候选框,我们按照模型给出的置信度由高到低对候选框进行排序。
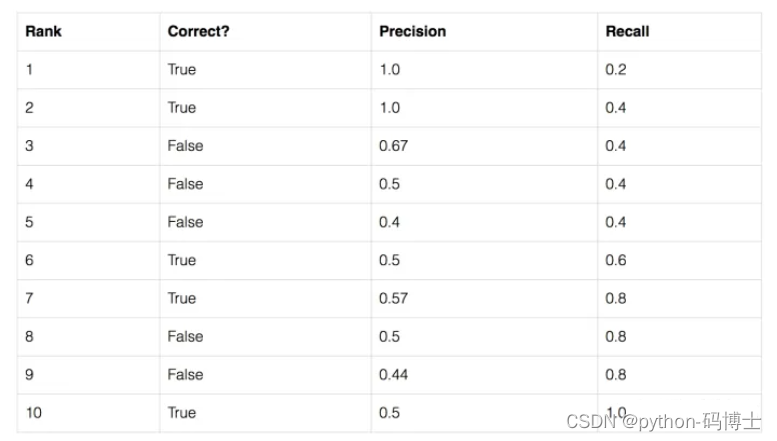
表格第二列表示该候选框是否预测正确(即这些候选框的iou值均大于0.5)第三列和第四列表示以该行所在候选框置信度为阈值时,Precision和Recall的值。我们以表格的第三行为例进行计算:
解题过程
首先这些数据是按照置信度由高到低进行排列的,所以以第三行为例进行计算时,前3行结果为True,后7行结果为False。非常好理解。
此时我们需要计算TP、FP、FN
还记得TP的定义吗?预测为正样本,检测也为正样本(真阳性),所以符合条件的有两个:第一、二行,因此TP=2
还记得FP的定义吗?预测为正样本,检测为负样本(假阳性),所以符合条件的只有第三行,因此FP=1
还记得FN的定义吗?预测为负样本,检测为正样本(假阴性),所以符合条件的有三个:第六、七、十行,因此FN=3
是不是还漏下一个TN?没有的!!!因为我们又不检测背景,计算时用不到。可以复习一下TP、TN 、FP 、FN这一块
还没有理解?看下面这张图
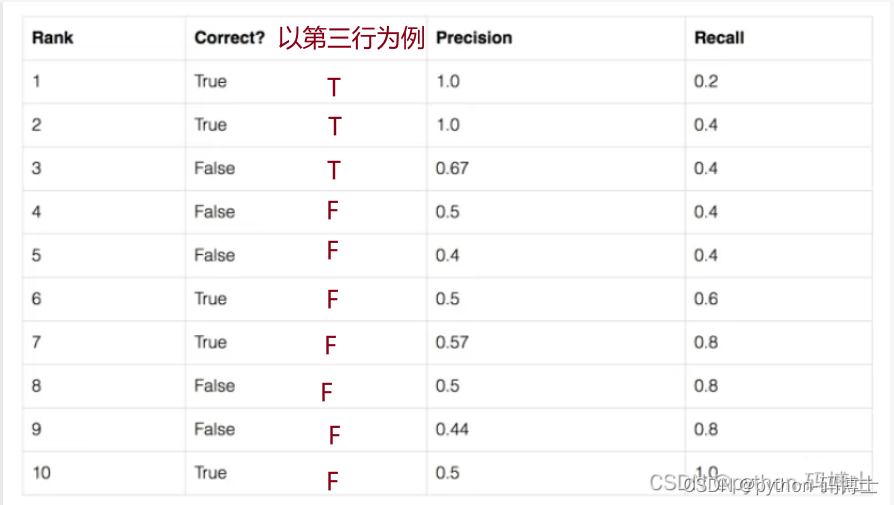
开始解题

由上表以Recall值为横轴,Precision值为纵轴,我们就可以得到PR曲线。我们会发现,Precision与Recall的值呈现负相关,在局部区域会上下波动。
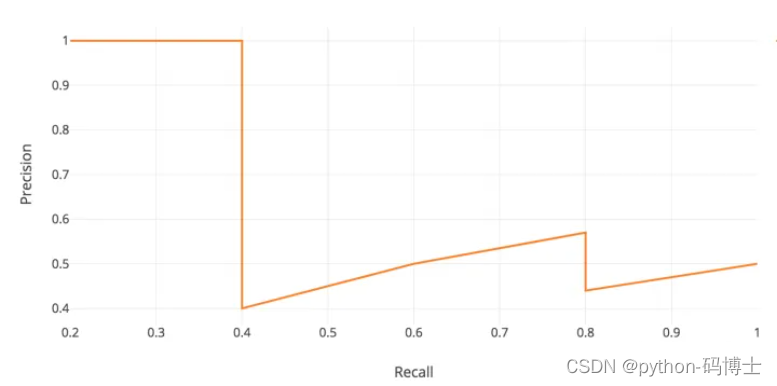
AP(Average Precision)
顾名思义AP就是平均精准度,简单来说就是对PR曲线上的Precision值求均值。对于pr曲线来说,我们使用积分来进行计算。

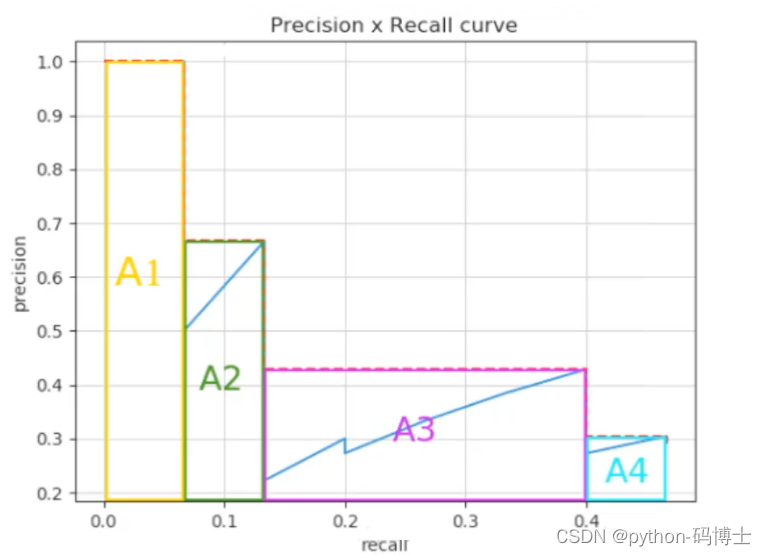
在实际应用中,我们并不直接对该PR曲线进行计算,而是对PR曲线进行平滑处理。即对PR曲线上的每个点,Precision的值取该点右侧最大的Precision的值。
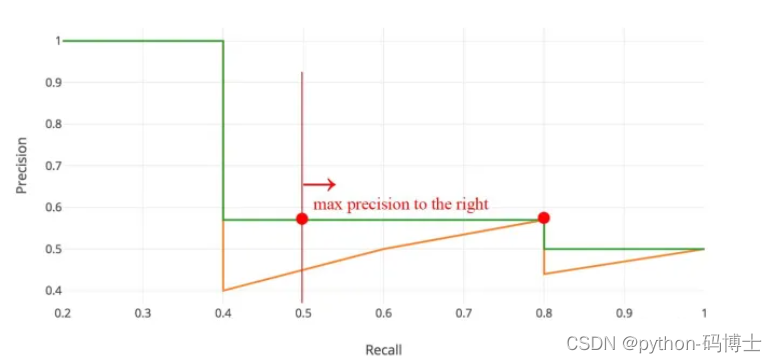
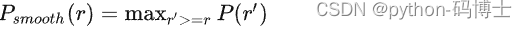
这里的公式有点唬人了,其实就是计算这个图的面积即为AP值:
AP = A1+A2+A3+A4…
mAP(mean Average Precision)
上述我们整个讨论过程只是以一个物体为例,注意到我们只检测了1类我们就得到了1根PR曲线,如果检测多类,那么每一类我们均可以得到一根PR曲线,也就是每类都会有1个AP值。
对所有类的AP值取平均就是mAP。
![[oeasy]python0035_ 整合shell编程_循环_延迟_清屏](https://img-blog.csdnimg.cn/img_convert/165e66291fd752e74e03b09a9eb594af.png)