RNN-T Training，RNN-T模型训练详解——语音信号处理学习（三）（选修三）

参考文献：

Speech Recognition (option) - RNN-T Training哔哩哔哩bilibili

2020 年 3月新番李宏毅人类语言处理独家笔记 Alignment Train - 8 - 知乎 (zhihu.com)

本次省略所有引用论文

一、如何将 Alignment 概率加和

对齐方式概率如何计算

概率加和计算原理

概率加和计算方式

二、RNN-T 的模型训练

模型训练思路

偏微分计算-1-展开变形

偏微分计算-2-第一个偏微分求解

偏微分计算-3-第二个偏微分求解

三、RNN-T 的模型测试（推理/解码）

目标函数的近似

实际操作

四、总结——LAS、CTC、RNN-T 模型比较

一、如何将 Alignment 概率加和

对齐方式概率如何计算

想要知道如何将所有的对齐方式的概率相加，我们就需要知道一条对齐方式的概率是怎么计算的。由于 HMM、CTC 和 RNN-T 的概率计算方式在本质上是一样的，因此我们下面的实验与计算全都基于 RNN-T。
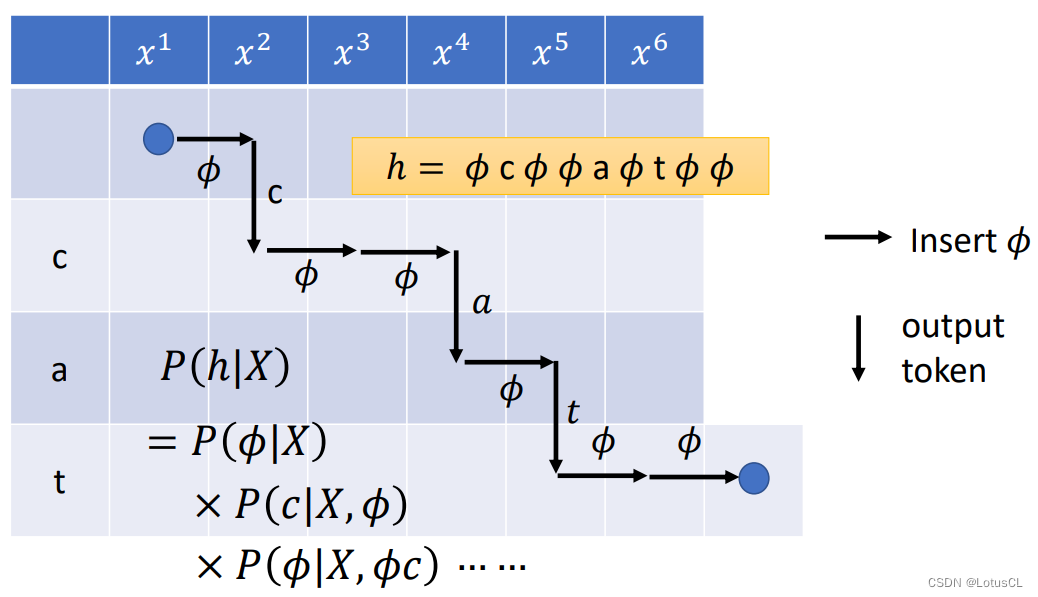
我们将一个 alignment 通过状态图的方式表现出，实际上，需要计算这个 alignment 的概率，只需要将所有位置的概率进行连乘就行。比如h = ∅c∅∅a∅t∅∅。P(h|X) 就等于每个位置的发射概率和转移概率的连乘，也就是第一次输出 ∅ 的概率，乘以给定 ∅，输出 c 的概率，乘以给定 ∅c，输出 ∅ 的概率……
我们将整个过程落实到实际操作当中去看看。首先，我们需要回顾 RNN-T 的架构。RNN-T 的一大神奇之处在于，它单独训练了一个 RNN，将已输出的 token 当作输入，去影响 RNN-T 接下来的输出。
我们使用 h 表示经过 encoder 的声学特征向量，图中上半部分蓝色的方块表示单独训练的 RNN。在起始阶段，没有产生任何的 token，我们就输入一个 <BOS (Begin of Sentence)>，让它产生 l0。我们把编码产生的h1，与l0一起输入给解码器，让它产生一个概率 p_{1,0}。这里的下标表示的意思为：输入第一个声学特征向量（1），没产生任何 token 时（0），RNN-T 产生出的概率分布。
那么 ∅ 落在句首的概率就可以计算了，也就是从 p_{1,0} 中采样出 ∅ 的概率。
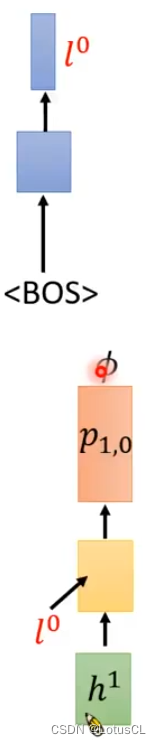
接下来我们需要计算有了 ∅ 以后产生 c 的概率。值得一提的是，刚刚产生的 ∅ 对我们的 RNN 并没有什么影响。因为 RNN 只吃产生的 token。不过，产生的 ∅ 会对 Encoder 产生影响，这代表当前的隐藏层向量已经被读完了，没啥价值了，需要切换下一个向量。
因此在下一步计算过程中，我们将 h2 和之前的 l0 一起输入编码器，输出得到概率 p_{2,0}。那么产生 c 的概率也就好算了，就是从概率分布 p_{2,0} 中采样得到 c 的概率。
接下来该计算有 ∅c 后产生 ∅ 的概率。由于我们刚刚输出了 token c，RNN 就会受到影响，输入 token c 以后产生 l1，而 Encoder 不变，因为它没有看到 ∅，所以不需要更换向量。因此我们最终将 l1 和 h2 丢给解码器，得到新的概率分布 p_{2,1}，从中我们可以得到我们需要的概率。
按照上面的过程，我们一直反复下去，最终我们就可以算出所有需要的概率，我们将所有的概率相乘，就是我们最终想得到的这一个 alignment 的概率。

概率加和计算原理

那么我们是怎么计算所有对齐方式的概率加和的呢？这就要归功于我们刚刚所说的 RNN-T 的神奇之处：使用单独的 RNN 来表示 token 之间的关系，而忽略 ∅ 的影响。这在后续的训练中大有帮助。
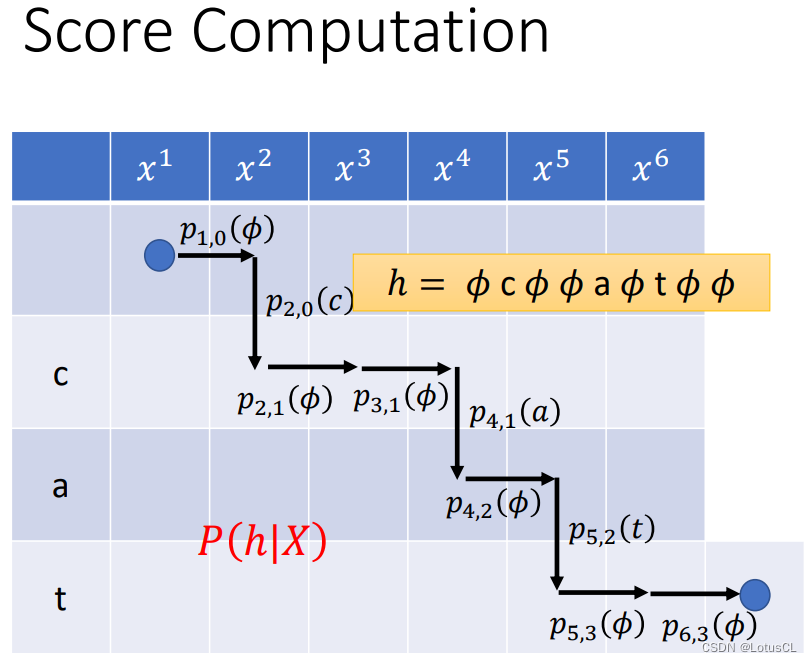
我们看下图，实际上下图中的每一个格子都可以对应到一个概率分布，由于刚刚定义的概率分布的下标分别表示读到的声学特征向量以及已输出的token数量，那么格子对应的概率分布就显而易见。比如图中给出了 p_{4,2} 的概率分布的格子，这就表示我们已经读到 x4，并且前边已经输出了两个 token ca。
而对于 p_{4,2}，需要计算之后产生 ∅ 或者 t 的概率都可以从中得到。
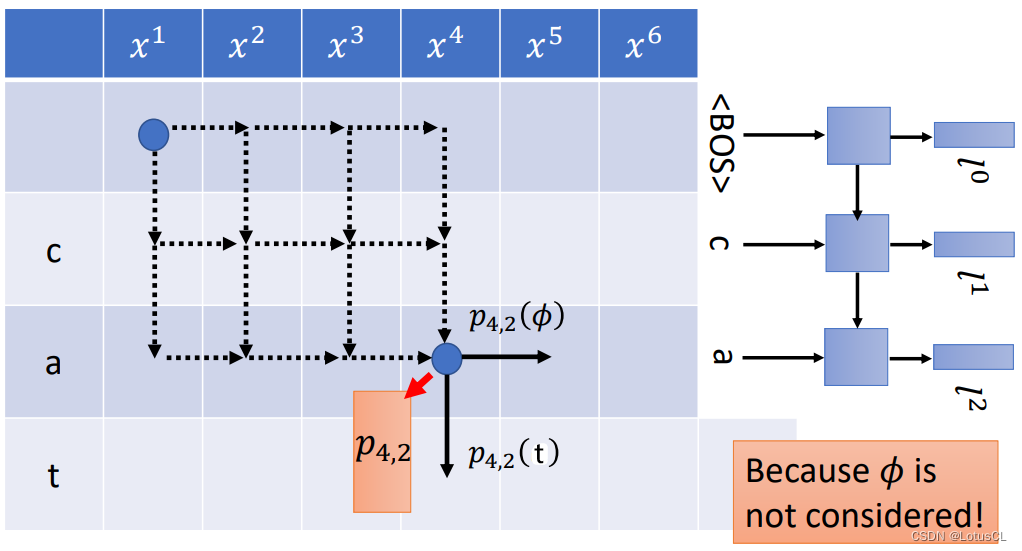
神奇之处在于，每一个格子代表的概率分布实际上都是固定的，它们不会受到如何走到当前格子的走法的影响，因为就其输入来说，无论怎么走，输入的都是 h4 和 l2。

概率加和计算方式

HMM 采用的是 forward 和 backward 算法来计算所有对齐方式的概率分数。而实际上，RNN-T 和 HMM 所用的方法也是一模一样的。
我们新定义一个变量 α_{i,j}，其表示已经读取了 i 个的声学特征向量，输出 j 个 token 的所有对齐方式的概率分数之和。比如 α_{4,2}，就是由读取 4 个声学特征向量，输出 2 个 token 的所有 Alignment 的分数相加之和。
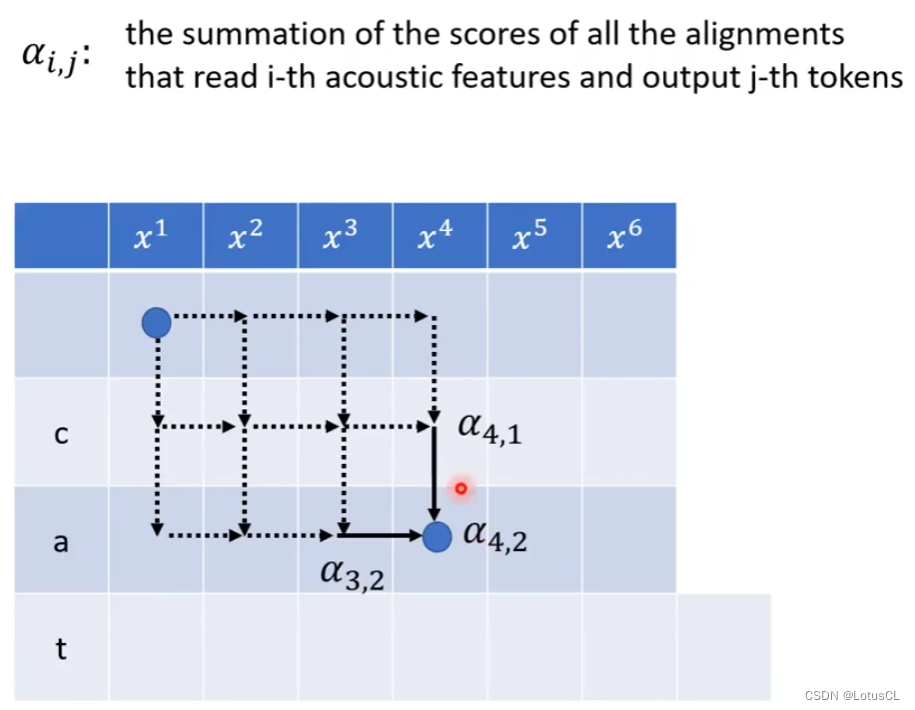
那么 α_{4,2} 有没有方法计算呢？有。我们可以通过 α_{4,1} 和 α_{3,2} 进行计算。事实上，在变成 α_{4,2} 之前，有两种可能，一种是读了 4 个声学特征向量，输出一个 token 了，准备输出下一个；还有一种可能是已经读了 3 个声学特征向量，产生了两个 token，准备读取下一个声学特征向量（产生 ∅ ）。假设我们的 α_{4,1} 和 α_{3,2} 已经计算出来了，则结合之前定义的 p_{i, j}，我们可以有：

$\alpha_{4,2} = \alpha_{4,1}p_{4,1}(a) + \alpha_{3,2}p_{3,2}(\varnothing)$
也就是 α_{4,1} 代表的所有 alignment 乘上之后产生 token a 的概率，加上 α_{3,2} 代表的所有 alignment 乘上之后产生 ∅ 的概率。
根据上面的式子，我们就可以得到一个基于动态规划的递推式，这样就能从左上角开始，一直算出最后一个格子的分数总和了。

二、RNN-T 的模型训练

我们刚刚讲述了如何去穷举所有的对齐方式进行概率总分计算，不过这一切都需要基于我们已经有了训练好的 RNN-T 的基础上。所以本节我们来了解一下如何训练 RNN-T。

模型训练思路

首先我们要明确我们的训练目标。假设 Y_hat 是我们的 Ground Truth，也就是正确的识别文本，那么也就是说我们希望学习到一组参数 θ，使得 Y_hat 的概率越大越好：

$\theta^* = \arg\max_\theta \log P_\theta(\widehat{Y}|X)$
那么我们如何 optimize 这个函数呢？当然是使用梯度下降法进行。所以我们下一个要解决的问题就是如何求取函数对参数求偏微分。

$\frac{\partial P(\widehat{Y}|X)}{\partial \theta} = ?$

偏微分计算-1-展开变形

我们将概率求解函数展开，它就像我们上面所说，是由一堆对齐概率加和而成的。而每一个对齐概率又是由某些概率相乘而得到的。
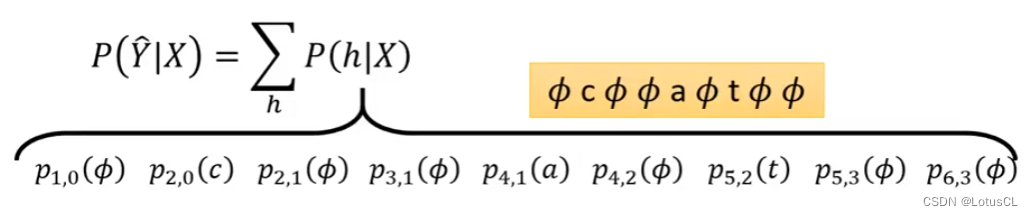
哪些概率？是由从起点到终点的某条路径上的每一个箭头所代表的概率，也就是在某个状态下产生某一个 token 的概率相乘得到的。因此，由这一系列所有的箭头相乘，然后相加，就最终得到了我们的概率。
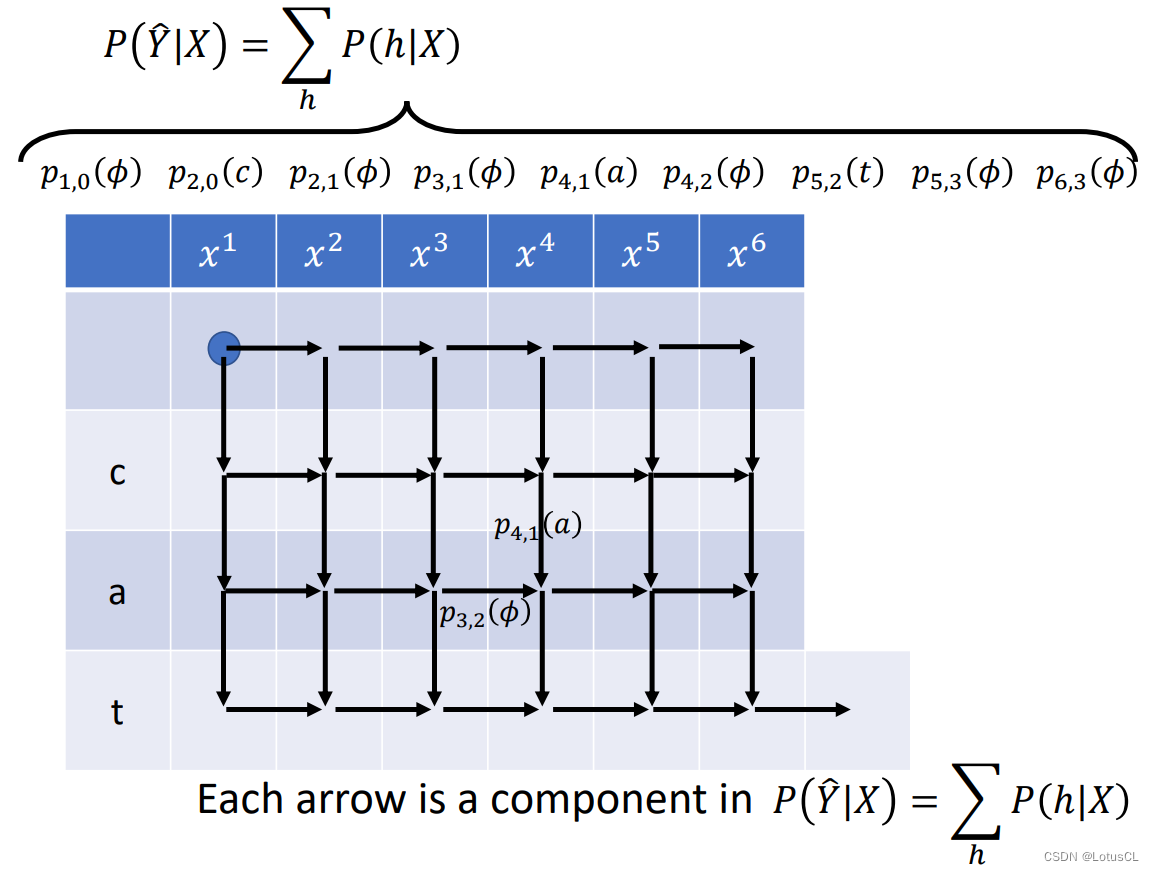
而这些产生某一个 token 的概率又受到模型参数 θ 的影响，目标概率又受到这些小概率的影响，所以我们可以先计算某个小概率对 θ 的偏微分，然后再计算目标概率对这些小概率的偏微分，和之前的相乘，然后再计算下一个小概率对 θ 的偏微分，乘上目标概率对小概率的偏微分……以此类推，最终将所有结果加和，就可以得到我们的目标式子，即：

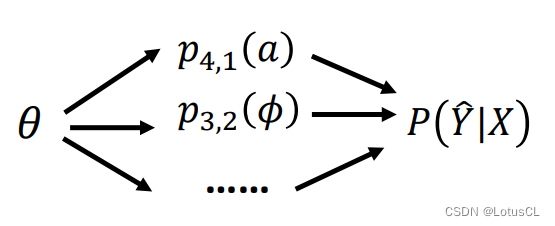
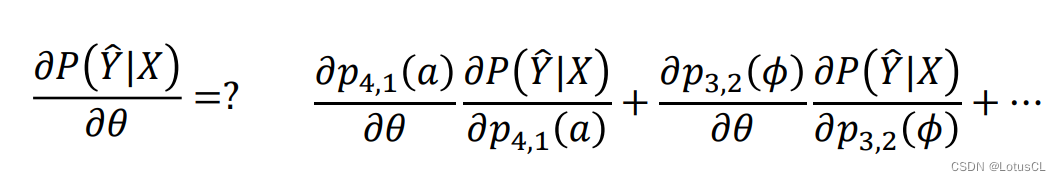
偏微分计算-2-第一个偏微分求解

好的，经过上面的变形，现在压力给到了如何计算小概率，即每个箭头代表的概率，对参数 θ 的偏微分。
我们以 p_{4,1}(a) 对 θ 的偏微分的计算作为例子。

$\frac{\partial p_{4,1}(a)}{\partial \theta} = ?$
其计算方式，或者说训练方式其实和普通模型一样，还是采用经典的 BPTT（Backpropagation Through Time，反向传播通过时间）时序的反向传播。一开始最右边的结果计算和标签的损失，反向传播传到编码器，再传到上面的解码器 RNN。

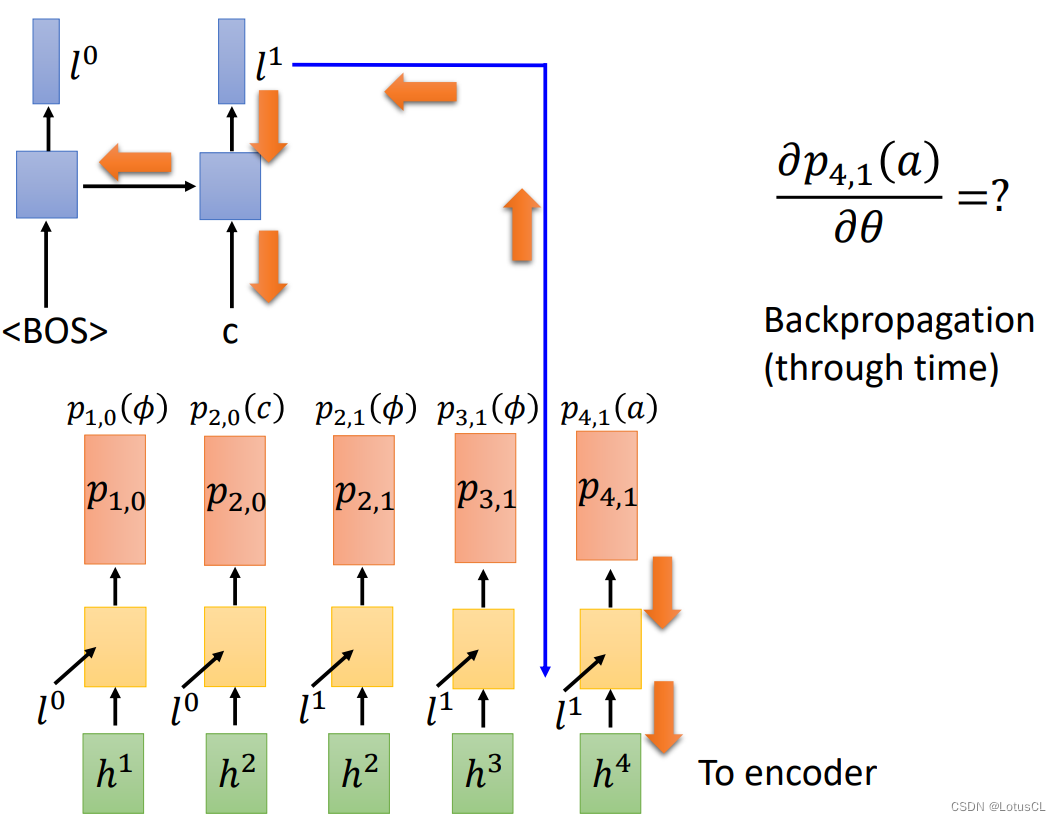
偏微分计算-3-第二个偏微分求解

第一个偏微分式子可以解了，下面压力来到了第二个偏微分式子上，也就是目标概率对每个箭头概率的偏微分。我们以计算对 p_{4,1} 的偏微分为例，公式如下：

$\frac{\partial P(\widehat{Y}|X)}{\partial p_{4,1}(a)} = ?$
首先，我们要把包含 p_{4,1} 的对齐方式和不包含 p_{4,1} 的对齐方式分开算：

$P(\widehat{Y}|X) = \sum_{h\space with\space p_{4,1}(a)}P(h|x) + \sum_{h\space without\space p_{4,1}(a)}P(h|x)$
由于第二项是没有 p_{4,1} 的，因此当做偏微分的时候，第二项就消失了。而第一项我们知道，是由很多箭头概率相乘相加得到的。既然有 p_{4,1}，我们就可以将它提取出来，如下图
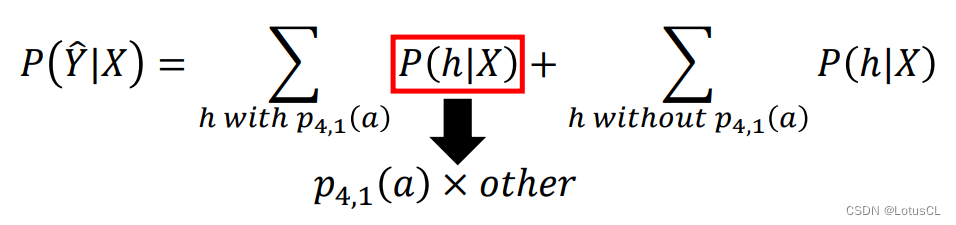
这样偏微分后就只剩提取出 p_{4,1} 之后的 other 了。并且我们还可以把 other 写成 P/p，然后再把这个 1/p 提出来，就可以了。
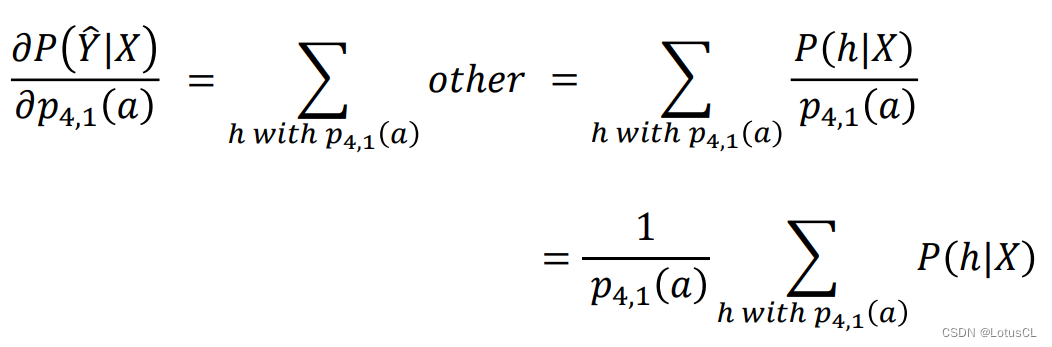
所以，问题就被转化成了计算带有 p_{4,1} 的对齐方式的概率之和。我们应该如何计算呢？此时，我们可以再引入另一个辅助变量 β_{i,j}，它与α_{i,j}很像，它表示从第 i 个声学特征开始且输出到第 j 个 token，在当前位置到结束的所有对齐方式分数之和。
β_{4,2} 如图所示，它表示已经产生了4个声学特征和输出两个 token 的情况下，在当前位置走到结尾为止的所有路径的分数总和。β_{i,j} 刚好是 α_{i,j} 的反过来。前面 α_{i,j} 对应着 HMM 的正向传播算法，这里 β_{i,j} 对应着 HMM 的反向传播算法。通过动态规划算法，于是我们有递推式，β_{i,j} = β_{i+1,j}p_{i,j} + β_{i,j+1}p_{i,j}。
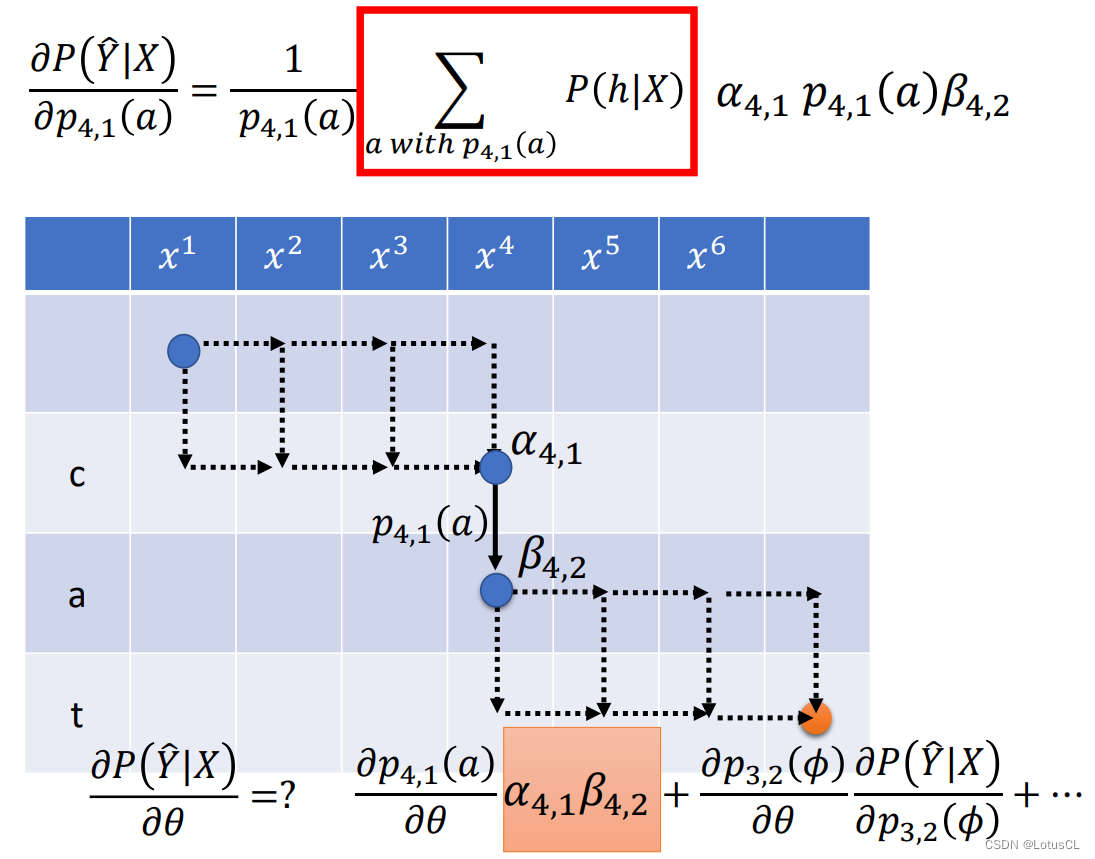
有了递推式以后，我们就可以将所有点的 β 值全部计算出来。而有了 α 和 β 的值以后，我们就可以计算带有 p_{4,1} 的对齐方式的概率之和了。我们看下图：所有从起始位置到 (4,1) 的候选对齐路径的分数和 α_{4,1} 乘上 p_{4,1}(a) 后，再乘上所有从位置 (4,2) 到终点的候选对齐路径的分数和 β_{4,2}，这就是所有包含 p_{4,1}(a) 的分数总和。
我们将式子带入，并乘上系数，p_{4,1}(a) 得到约分，最终的偏微分结果就是 α_{4,1}β_{4,2}。
因此带入最终的式子后，就能计算全部候选对齐的得分对模型参数的梯度。然后反向传播更新模型参数进行训练。我们就可以进行正常训练了。

三、RNN-T 的模型测试（推理/解码）

目标函数的近似

训练好模型了以后，我们就可以进行模型的使用了。我们的目标函数如下，也就是找到一个 Y，使得 P of Y given X 达到最大值，这个 Y 就是模型语音辨识的结果。

$Y^* = \arg\max_Y \log{P(Y|X)}$
这实际上不是一个简单的问题。理想状态下我们需要穷举所有的 Y，来计算概率，然而别说穷举不容易实现，就连计算概率都是大量的对齐方式概率相加之和，就更不容易了。
所以我们采用一些近似估计的方法，首先就是对 “将所有对齐方式概率加和作为分数” 这一条进行近似。我们不把所有的候选对齐分数加起来，而是选取每一个Y中，分数最高的那个对齐方式的概率作为分数。不过，这个近似需要基于这样一个事实：概率最大的对齐方式要比其他的对齐方式要大很多。那事实真的是这样吗？（老师：反正我信了）
我们将概率最大的对齐方式记作 h*，然后用 h* 进行 inverse，找到其对应的 Y*，就是最终解码的结果啦。计算 P of h given X 的方式我们在之前都有讲过，这里在图中呈现回顾一下，不再用文字赘述。

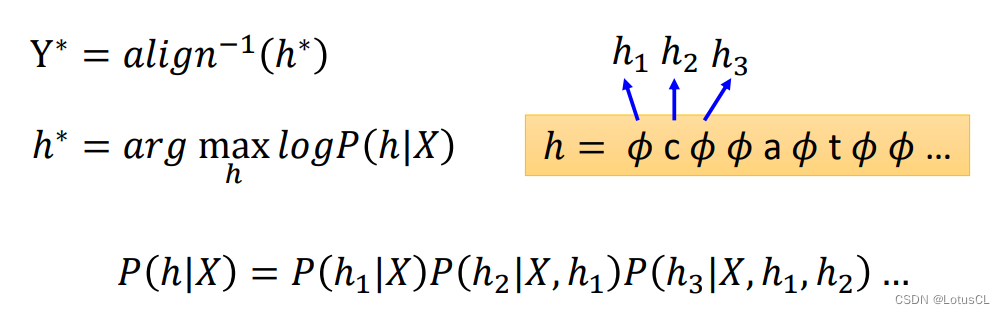
实际操作

实际中要怎么找一个概率最高的对齐方式呢？RNN-T 每一个时间步都会跑出一个概率分布。我们把每个概率分布中，概率最大的那个 token 取出来，就是 h* 的一个近似。不过，每次都取概率分布中概率最大的，不见得会使得整个对齐方式的概率是最大的（原因距离可以看束搜索 Beam Search 讲解）。不过没有关系，我们照样可以采用 Beam Search 的方法来得到更准确的结果。

四、总结——LAS、CTC、RNN-T 模型比较

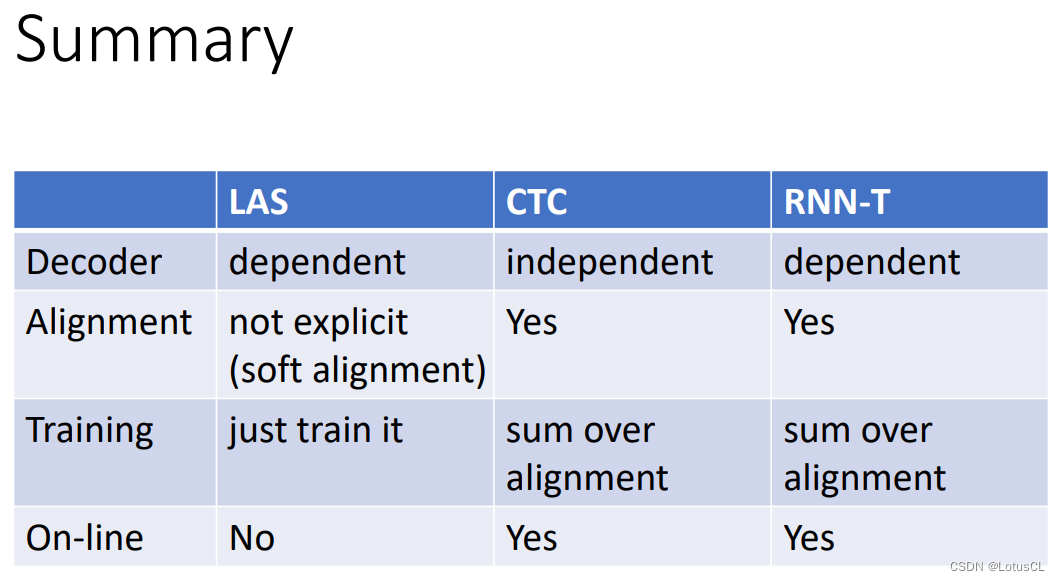
我们看下面这张表。在解码部分，LAS 和 RNN-T 会考虑前面的时序对当前时序的影响。而 CTC 并不会考虑之前的时间步已经生成出来的token。所以 LAS 和 RNN-T 在解码部分是相对比较强的。
在对齐部分，CTC 和 RNN-T 都是需要考虑对齐的。而因为中间的注意力层，LAS不用显式地考虑对齐，而是采用 soft alignment，使用注意力机制来找出语音和文字之间的关系。
在训练部分，LAS 只需要直接训练就行，而 CTC 和 RNN-T 则需要将所有的对齐方式概率相加，比较麻烦。
对于语音识别模型，在线识别（实时识别）也是一个很重要的功能，使用者一边说一边就能跑出语音辨识的结果。对于 LAS，由于注意力一次要看全部，也就是需要等语者说完才能进行推理，因此 LAS 不能在线识别。而 CTC 和 RNN-T 都是可以的，之前有说过，Pixel 的语音助手就是使用 RNN-T 进行语音识别的。