文章目录

• • 🍷371. 两整数之和
  • • 🥙题目
    • 🍅算法原理
    • 🍆代码实现
  • 🍸137. 只出现一次的数字 II
  • • 🧆题目
    • 🫒算法原理
    • 🥔代码实现
  • 🍹面试题 17.19. 消失的两个数字
  • • 🥚题目
    • 🥥算法原理
    • 🥕代码实现

🍷371. 两整数之和

🥙题目

题目链接：371. 两整数之和 - 力扣（LeetCode）

给你两个整数 a 和 b ，不使用 运算符 + 和 - ，计算并返回两整数之和。

示例 1：

输入：a = 1, b = 2
输出：3

示例 2：

输入：a = 2, b = 3
输出：5

提示：

• -1000 <= a, b <= 1000

🍅算法原理

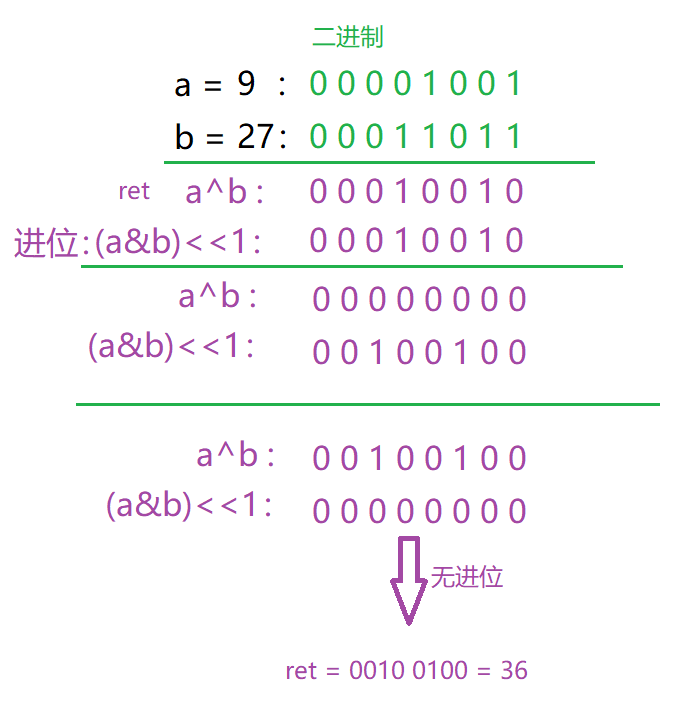
这种不能使用+或者-操作符，大概率就是用位运算来操作。

异或运算又叫无进位相加，而按位与全1为1，又可以找出需要进位的位置，然后让这个位置往左移一位即可表示进位。

然后一直循环这个操作，直到进位的结果为0为止

🍆代码实现

class Solution {
public:
    int getSum(int a, int b)
    {
        while(b!=0)
        {
            int x = a^b;	//无进位相加
            //unsigned int 防止溢出
            unsigned int carry = (unsigned int)(a&b) << 1;    //进位
            a = x;
            b = carry;
        }
        return a;
    }
};

运行结果：

🍸137. 只出现一次的数字 II

🧆题目

题目链接：137. 只出现一次的数字 II - 力扣（LeetCode）

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现三次。 请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

示例 1：

输入：nums = [2,2,3,2]
输出：3

示例 2：

输入：nums = [0,1,0,1,0,1,99]
输出：99

提示：

• 1 <= nums.length <= 3 * 104
• -231 <= nums[i] <= 231 - 1
• nums 中，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次

🫒算法原理

假设出现一次的数是a，其他的数都是出现三次，那么这所有的数的其中一个比特位，只会有四种情况：

1. 3n个0 + 0，比特位总和为0
2. 3n个0 + 1，比特位总和为1
3. 3n个1 + 0，比特位总和为3n
4. 3n个1 + 1，比特位总和为3n+1

我们将这些数通通取模%3，此时的情况是和只出现一次的那个数的比特位

此题还能拓展一下，即一个数出现一次，其他数均出现n次，我们这里只需要%n即可

🥔代码实现

class Solution {
public:
    int singleNumber(vector<int>& nums)
    {
        int ret = 0;
        for(int i=0;i<32;i++)
        {
            int sum = 0;
            for(auto e:nums)    //统计nums中所有数第i位的和
                if((e>>i)&1 == 1)   sum++;
            
            sum%=3;
            if(sum == 1)    ret |= 1<<i;
        }
        return ret;
    }
};

运行结果：

🍹面试题 17.19. 消失的两个数字

🥚题目

题目链接：面试题 17.19. 消失的两个数字 - 力扣（LeetCode）

给定一个数组，包含从 1 到 N 所有的整数，但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗？

以任意顺序返回这两个数字均可。

示例 1:

输入: [1]
输出: [2,3]

示例 2:

输入: [2,3]
输出: [1,4]

提示：

• nums.length <= 30000

🥥算法原理

这里可以将思路转换，假设缺少的两个数为a和b，我们将nums看作一个整体，[1,N]看作整体，然后将这两个合并，就转换成了这一堆数中，只有a和b出现了一次，其他的数均出现了两次

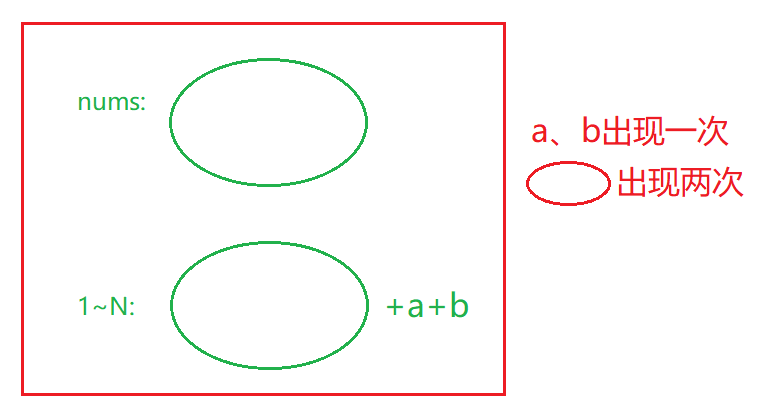
将这两组数异或之后得到一个数tmp，这个是就是a^b的结果，然后只需要将a和b分开即可。

根据异或的规则，相同为0，相异为1，我们要找到tmp中一个比特位为1的位置。然后将所有的数划分为两大类，即

• x为0
• x为1

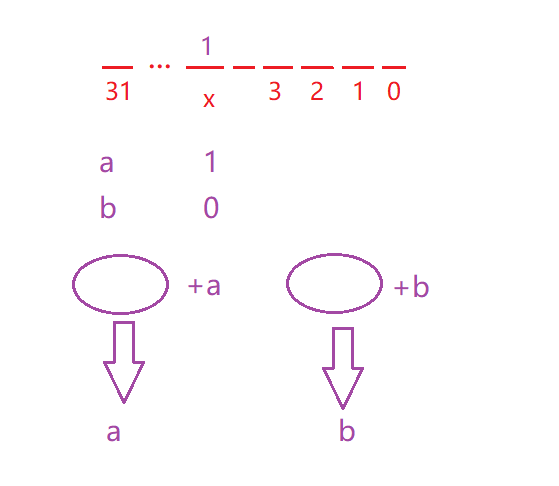
所以整体就是分为三步：

1. 将所有的数异或在一起，得出一个tmp
2. 找到tmp中，比特位为1的那一位
3. 根据x位的不同，划分成两类异或

🥕代码实现

class Solution {
public:
    vector<int> missingTwo(vector<int>& nums)
    {
        //异或所有数
        int tmp = 0;
        for(auto e:nums)    tmp^=e;
        for(int i=1;i<=nums.size()+2;i++) tmp^=i;

        //找出比特位为1的位置
        int diff = 0;
        while(1)
        {
            if(((tmp>>diff)&1) == 1)  break;
            else    diff++;
        }

        //分类异或
        int a = 0;
        int b = 0;
        for(auto e:nums)
        {
            if(((e>>diff)&1) == 1)    a^=e;
            else    b^=e;
        }
        for(int i=1;i<=nums.size()+2;i++)
        {
            if(((i>>diff)&1) == 1)    a^=i;
            else    b^=i;
        }
        return {a,b};   
    }
};

运行结果：