一、Nim游戏

1、题目

2、结论

这里直接说结论：
假设有$n$堆石子，对于第$i$堆石子，石子个数是$a_i$。
那么我们可以通过以下结论判断先手是否必赢：

3、结论验证

我们可以简单验证一下结论：
我们主要从两个角度入手，

先手必赢状态必定可以让对手为先手的时候，所面对的局面是必输状态。

证明：

---

第二件事我们要验证的就是，

我本身处于先手必输的状态，当轮到对方的时候，对方不可能也面对必输的状态。

证明：

如果我取出石子，必定会让某堆的石子数目发生变化，不变化的时候，抑或结果是0，变化之后抑或结果一定不是0。

如果我拿走了石子抑或结果还是0，那么说明我拿走前后该堆石子数目没变，说明我拿了0个，但是这是违法操作。

既然不可能是0，那么对方面对的就一定是必赢的状态。

4、代码

代码实现的话，我们只要看抑或结果是不是0就行了。

#include<iostream>
using namespace std;
int main()
{
    int res=0;
    int n=0;
    cin>>n;
    while(n--)
    {
        int a;
        scanf("%d",&a);
        res^=a;
    }
    if(res)puts("Yes");
    else puts("No");
}

二、集合——Nim游戏

1、问题

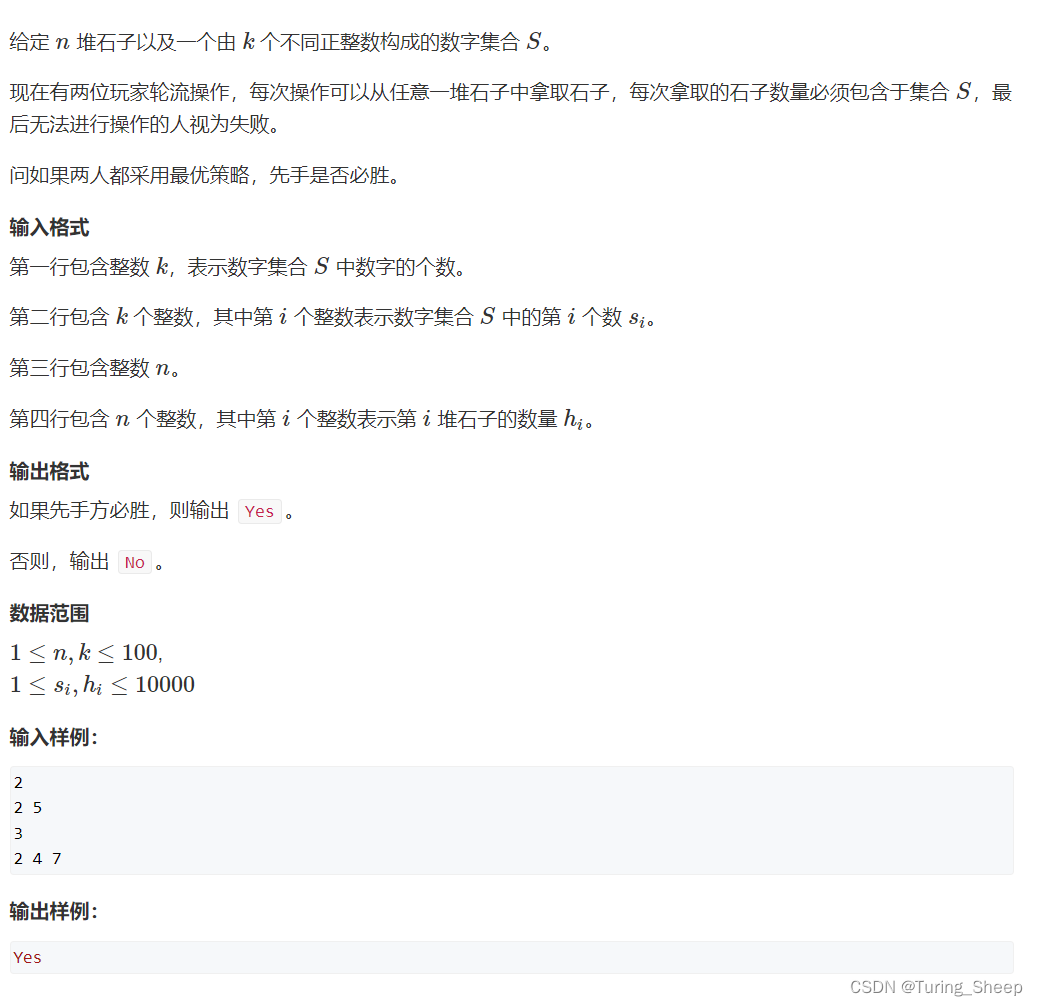
2、思路—SG()函数

我们这里再引入一个$SG()$函数的概念，而这个函数的定义需要根据一个有向无环图定义。

我们知道，我们比赛时的每一个状态都可以看作一个点，我们的操作可以看作一个有向边，经过有向边，我们可以到达下一个状态。

我们看下面这个图：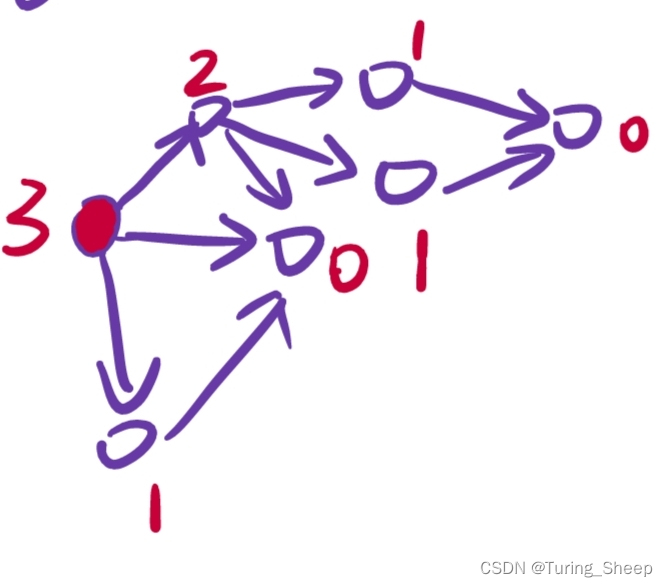
我们把最终状态变成0，而这里还是要用到我们的nim中的结论。

如果我处于了最终的状态，意思就是我无法进行操作了，那么就说明处于一种必输的状态，所以我们把所有的终点都标记成0。

然后，我们倒退，上一个节点的$SG()$函数值等于一个最小的大于等于0值，并且这个最小的自然数值不能是它所有可能的下一个状态的$sg()$的函数值。比如，一个节点连接着$sg()$函数值为$0,1,2$的点，那么当前的点就只能取$3$，如果所连的点是$1,2$，那么我可以是$0$。

$sg()$函数的意义同刚刚的结论一样：

如果函数值是0，说明当前是先手必输状态，如果函数值非0，说明当前的状态是先手必赢状态。

那么如我们的每一堆都可以画出这样一个图，那么思路就是，我们根据操作画出所有的情况，构成一个有向无环图，然后逆推$SG()$函数。如下图：

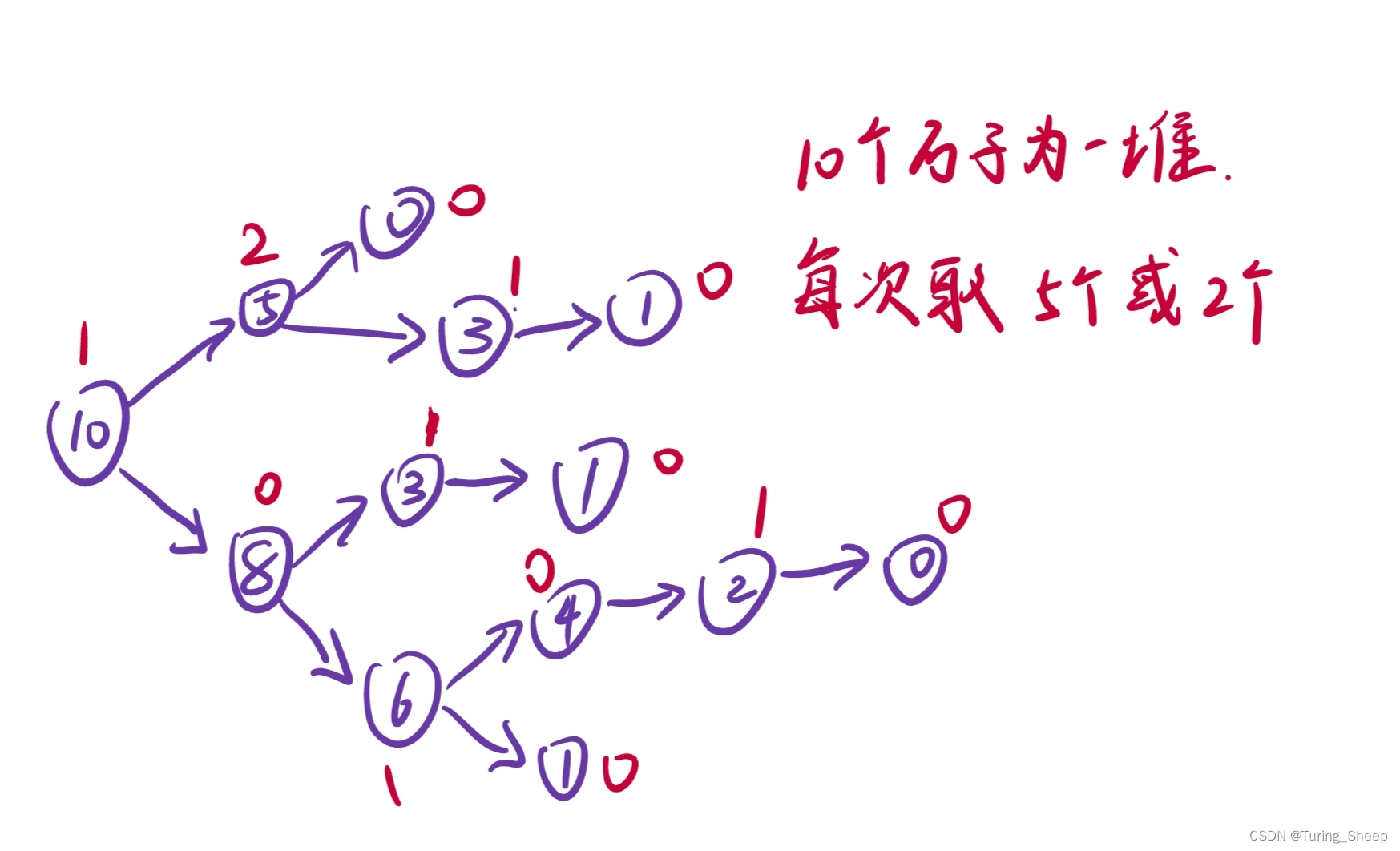
那么我们对每堆石子都进行上述的操作，然后画出$n$个图，然后我们对每个图的起点的$SG()$函数值进行抑或操作，看最终是否等于0，等于0说明先手必输，不等于0说明先手必赢。

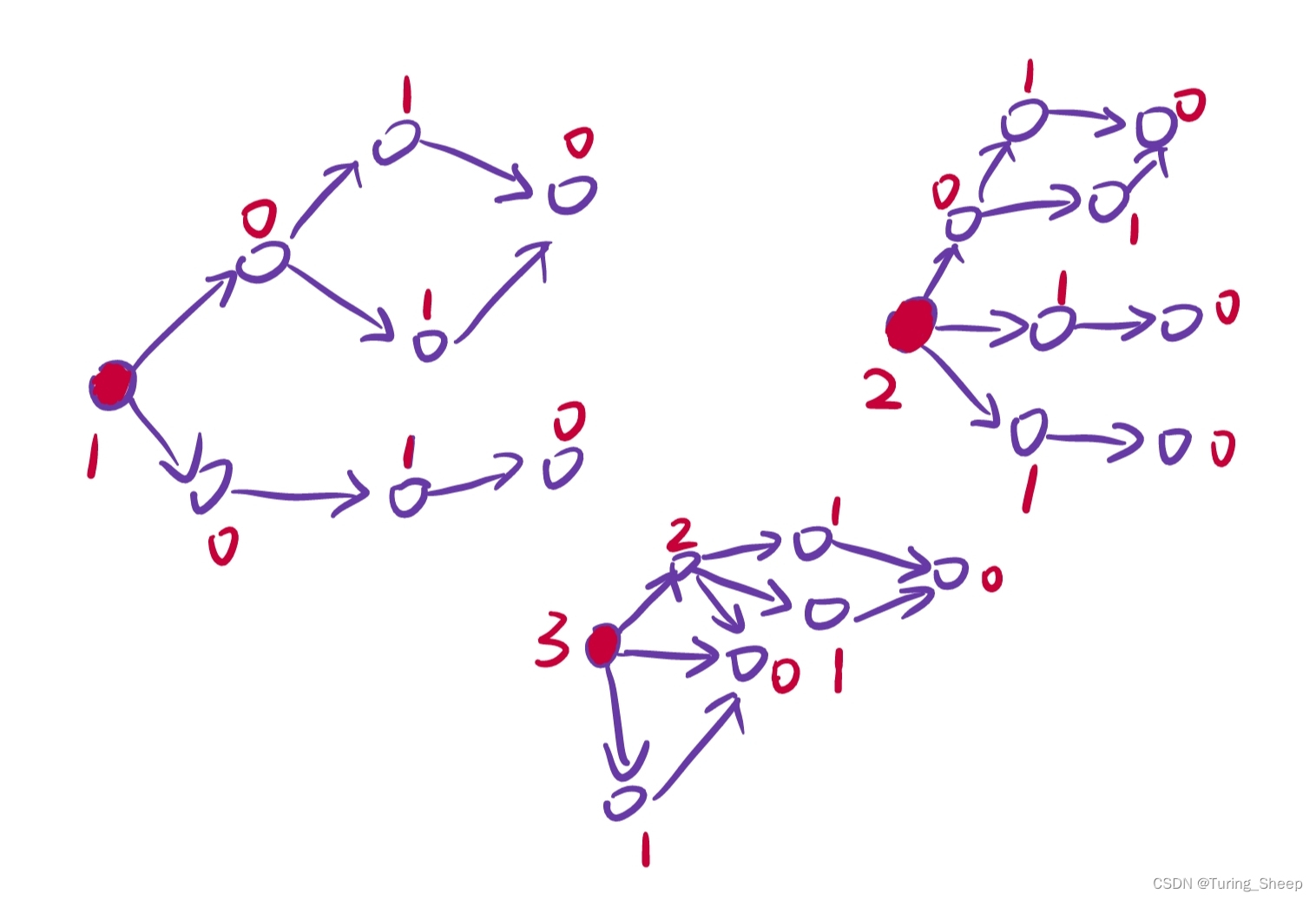
2、代码实现（记忆化搜索）

#include <cstring>
#include <iostream>
#include <unordered_set>
using namespace std;
const int N = 110, M = 10010;
int n, m;
int s[N], f[M];
int sg(int x)
{
    if (f[x] != -1) return f[x];
    unordered_set<int> St;
    for (int i = 0; i < m; i ++ )
    {
        int sum = s[i];
        if (x >= sum) St.insert(sg(x - sum));
    }
    for (int i = 0; ; i ++ )
        if (!St.count(i))
            return f[x] = i;
}
int main()
{
    cin >> m;
    for (int i = 0; i < m; i ++ ) cin >> s[i];
    cin >> n;
    memset(f, -1, sizeof f);
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res) puts("Yes");
    else puts("No");
    return 0;
}