Java中的Integer.bitCount浅析

原文链接

问题

有一个整数x,我们需要统计该整数的二进制表示中包含的1的个数。这个也被称为汉明重量（Hamming weight）。

例如，整数13的二进制表示是1101，其中有3个1，因此统计出的结果是3。

思考

看到这个问题的时候可能的想法就是遍历一遍这个二进制数位并统计结果。

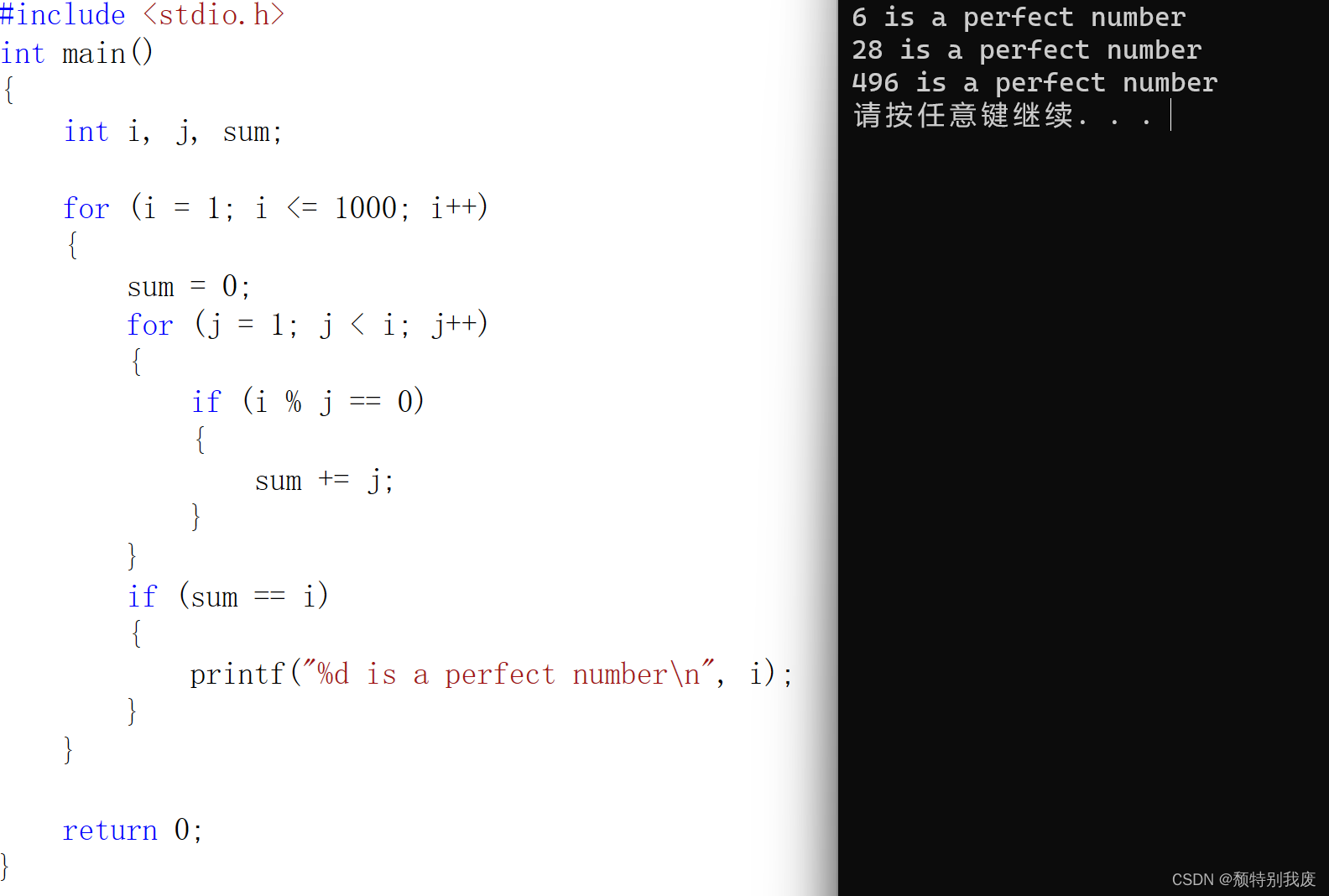
对于统计32位的整数，下面是其中的一种做法：

 int bitCount(int x) {
        int count = 0;
        for (int i = 0; i < 32; i++) {
            int t = x & 1;
            //count+=t;
            if (t == 1) {
                count++;
            }
            x >>= 1;
        }
        return count;
    }

这种做法时间复杂度是O(n)，n是二进制数的位数

Integer.bitCount

在Java中也有提供统计整数数位1数量的方法Integer.bitCount，下面是它的源码:

public static int bitCount(int i) {
        // HD, Figure 5-2
        i = i - ((i >>> 1) & 0x55555555);
        i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
        i = (i + (i >>> 4)) & 0x0f0f0f0f;
        i = i + (i >>> 8);
        i = i + (i >>> 16);
        return i & 0x3f;
    }

这个方法的代码第一眼看过去有点看不明白，但是我们可以很直观得看到这个方法里面并没有用到循环统计的方法，而是进行了几步位运算和算数运算就可以统计出来了，它是怎么做到的呢？

解释

直接举个例子:
对于数值为1822569234的32位整数，它的32位二进制表示为01101100101000100011001100010010，其中有13个1，计算过程如下:

对上图做出解释：

1. 首先我们对二进制进行分组，每组一个比特位，这样一开始有32组，假设为每个分组编号，从左到右即分组1，分组2，......，分组32
2. 接着将每两个相邻的组进行求和，即分组1和分组2，分组3和分组4，…，分组31和分组32，这样我们就可以先求出每两位中1的数量

0+0=00(等于十进制0)
0+1=01或1+0=01(等于十进制1)
1+1=10（等于十进制2）

3. 结果放到求和组的数位上，形成新的分组，每组中有两个比特位，这些组的值就是每两个比特位中1的数量，可以重新编号分组1，分组2......分组15，分组16
4. 继续对相邻的组进行求和，组成每4个比特位为一组的分组，依此类推，直到每32位为一组就是答案了。

这个过程其实利用了分治的思想，将一个大的问题，分解为多个小的子问题，先对子问题进行求解，最后将子问题合并得出结果。

这个过程用代码写出来如下:

  static int bitCount(int x) {
        x = (x & 0b01010101010101010101010101010101) + ((x >> 1) & 0b01010101010101010101010101010101);
        x = (x & 0b00110011001100110011001100110011) + ((x >> 2) & 0b00110011001100110011001100110011);
        x = (x & 0b00001111000011110000111100001111) + ((x >> 4) & 0b00001111000011110000111100001111);
        x = (x & 0b00000000111111110000000011111111) + ((x >> 8) & 0b00000000111111110000000011111111);
        x = (x & 0b00000000000000001111111111111111) + ((x >> 16) & 0b00000000000000001111111111111111);
        return x;
    }

在大部分编程语言中要表示二进制数，可以在其前面加上0b或0B前缀。

对于上述代码中，第一行就是求每个分组是1个比特位时，相邻分组的和。(x & 0b01010101010101010101010101010101)就是将分组1的值置零，保留分组2的值；分组3的值置零，保留分组4的值…依此类推。((x >> 1) & 0b01010101010101010101010101010101)
就是先将相邻分组中的第一个分组移到自己相邻的分组，即分组1的值移动到分组2，分组2到分组3,分组3到分组4…，之后再将分组1,分组3,分组5…等置零，避免影响求和的结果。最后将(x & 0b01010101010101010101010101010101)与((x >> 1) & 0b01010101010101010101010101010101)求和，就是第一次相邻分组的求和结果了，接着后面只是每个分组的比特位变多了，过程还是一样，最终得到32个比特位为一组时就是结果了。

这样的算法时间复杂度就是$O({\log }_{2}n)$，n是二进制数的位数

我们可以将上面的代码中的数值用十六进制表示：

static int bitCount(int x) {
        x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
        x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
        x = (x & 0x0F0F0F0F) + ((x >> 4) & 0x0F0F0F0F);
        x = (x & 0x00FF00FF) + ((x >> 8) & 0x00FF00FF);
        x = (x & 0x0000FFFF) + ((x >> 16) & 0x0000FFFF);
        return x;
    }

和Java中的进行比较

public static int bitCount(int i) {
        // HD, Figure 5-2
        i = i - ((i >>> 1) & 0x55555555);
        i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
        i = (i + (i >>> 4)) & 0x0f0f0f0f;
        i = i + (i >>> 8);
        i = i + (i >>> 16);
        return i & 0x3f;
    }

很明显这个和Java中的bitCount还是不一样呀？其实Java中的bitCount是在这个代码基础上减少了一些不必要的运算的结果。

1. 第一行 x = (x & 0x55555555) + ((x >> 1) & 0x55555555)其实可以等效于x = x - ((x >> 1) & 0x55555555)，可以减少一次与运算
2. 第二行，这个是求每个分组有2个比特位的时候的和，因为分组n和分组n+1相加的结果最大是4，二进制表示即100,超过分组n+1的2比特位，所以只能保留原样
3. 第三行，这个是求每个分组有4个比特位的时候的和，因为分组n和分组n+1相加的结果最大时8，二进制表示即1000，没有超过分组n+1的4比特位，所以可以先对原来的数字和移位的数字进行求和，之后要对分组n的位置置零，避免对后面求和结果造成影响，也就是需要与上0x0F0F0F0F。
4. 第四行，这个是求每个分组有8个比特位的时候的和，因为分组n和分组n+1相加的结果最大时16，二进制表示即10000，没有超过分组n+1的8比特位，所以可以和第三行那样先求和。而且32比特位中1的数量最大也就是32个，二进制表示即100000，只有6个比特位，所以结果也不会超过8个比特位，不需要对分组n置零，就是不需要与运算。
5. 第五行，这个是求每个分组有16个比特位的时候的和，同第四行一样可以直接求。
6. 最后的结果保存在低位的6个比特位置上，所以需要与上0b111111，换成十六进制就是0x3F。

拓展

理解了32个数位的做法，那推广到64个数位也可以利用上述的思想。

下面是Java中Long.bitCount的源码

public static int bitCount(long i) {
        // HD, Figure 5-2
        i = i - ((i >>> 1) & 0x5555555555555555L);
        i = (i & 0x3333333333333333L) + ((i >>> 2) & 0x3333333333333333L);
        i = (i + (i >>> 4)) & 0x0f0f0f0f0f0f0f0fL;
        i = i + (i >>> 8);
        i = i + (i >>> 16);
        i = i + (i >>> 32);
        return (int)i & 0x7f;
     }