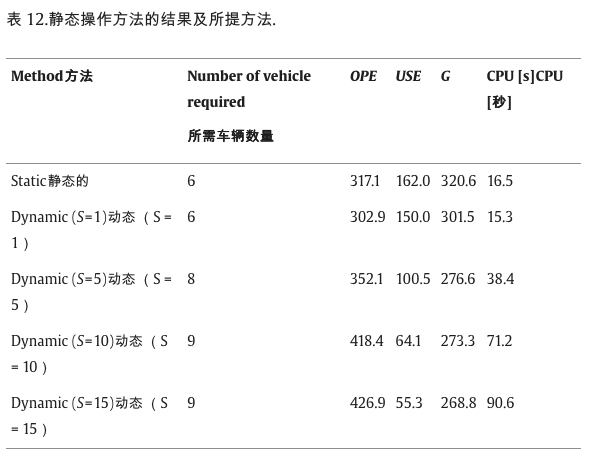
极限学习机(ELM, Extreme Learning Machines)是一种前馈神经网络,ELM 不需要基于梯度的反向传播来调整权重,而是通过 Moore-Penrose generalized inverse来设置权值。
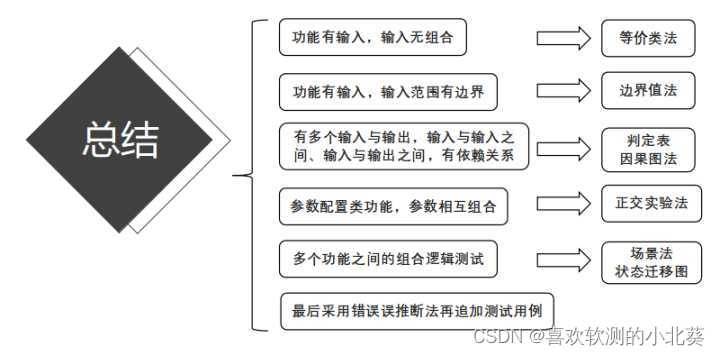
标准的单隐藏层神经网络结构如下:
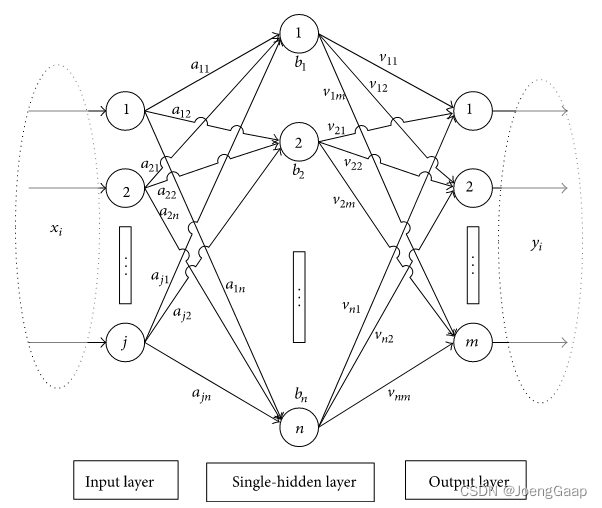
单隐藏层神经网络 | ELM网络
- 输入值乘以权重值 | 输入值乘以权重值
- 加上偏置值 | 加上偏置值
- 进行激活函数计算 | 进行激活函数计算
- 对每一层重复步骤1~3 | ×
- 计算输出值 | 计算输出值
- 误差反向传播 | 矩阵逆运算
- 重复步骤1~6 | ×
极限学习机就是没有反向传播的简单神经网络,反向传播部分使用矩阵逆运算计算权重。
极限学习机前向传播:
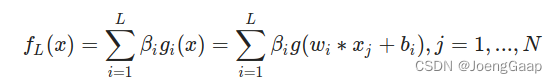
L 是隐藏单元的数量;N 是训练样本的数量;
beta 是第 i 个隐藏层和输出之间的权重向量(相当于图中的v);w 是输入和隐藏层之间的权重向量(相当于图中的a);
g 是激活函数;b 是偏置向量;x 是输入向量
可将这个函数看成:
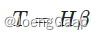
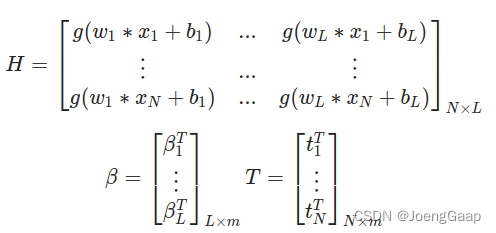
m 是输出的数量;
H 是隐藏层输出矩阵;
T 是训练集目标矩阵;
H是可逆的,T是已知的(因为它是已知标签结果)
||Hβ’-T||=min||Hβ-T||=0,即β’=H^-1T.。
所以这里需要求解的就是β的值。
ELM 算法主要过程:
- wi,bi,i=1,L 随机初始化
- 计算隐藏层输出
- H 计算输出权重矩阵
极限学习机 Extreme Learning Machines 介绍
python代码实现
class RELM_HiddenLayer:
"""
正则化的极限学习机
:param x: 初始化学习机时的训练集属性X
:param num: 学习机隐层节点数
:param C: 正则化系数的倒数
"""
def __init__(self, x, num, C=10):
row = x.shape[0]
columns = x.shape[1]
rnd = np.random.RandomState()
# 权重w
self.w = rnd.uniform(-1, 1, (columns, num))
# 偏置b
self.b = np.zeros([row, num], dtype=float)
for i in range(num):
rand_b = rnd.uniform(-0.4, 0.4)
for j in range(row):
self.b[j, i] = rand_b
self.H0 = np.matrix(self.softplus(np.dot(x, self.w) + self.b))
self.C = C
self.P = (self.H0.H * self.H0 + len(x) / self.C).I
# .T:转置矩阵,.H:共轭转置,.I:逆矩阵
@staticmethod
def sigmoid(x):
"""
激活函数sigmoid
:param x: 训练集中的X
:return: 激活值
"""
return 1.0 / (1 + np.exp(-x))
@staticmethod
def softplus(x):
"""
激活函数 softplus
:param x: 训练集中的X
:return: 激活值
"""
return np.log(1 + np.exp(x))
@staticmethod
def tanh(x):
"""
激活函数tanh
:param x: 训练集中的X
:return: 激活值
"""
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
# 分类问题 训练
def classifisor_train(self, T):
"""
初始化了学习机后需要传入对应标签T
:param T: 对应属性X的标签T
:return: 隐层输出权值beta
"""
if len(T.shape) > 1:
pass
else:
self.en_one = OneHotEncoder()
T = self.en_one.fit_transform(T.reshape(-1, 1)).toarray()
pass
all_m = np.dot(self.P, self.H0.H)
self.beta = np.dot(all_m, T)
return self.beta
# 分类问题 测试
def classifisor_test(self, test_x):
"""
传入待预测的属性X并进行预测获得预测值
:param test_x:被预测标签的属性X
:return: 被预测标签的预测值T
"""
b_row = test_x.shape[0]
h = self.softplus(np.dot(test_x, self.w) + self.b[:b_row, :])
result = np.dot(h, self.beta)
result = np.argmax(result, axis=1)
return result
基于python的ELM(极限学习机)分类及回归实现(附带自己数据链接及推导)