冒泡排序
基本思想
先将第一个记录与第二个记录比较,将较大的记录放到第二个位置上,之后再将第二个记录与第三
个记录比较,将较大的记录放到第三个位置上,如此类推,知道比较完最后一个位置,此时注意到
最后一个位置是整个记录表中最大的记录了。随后我们进行第二趟比较,但是此时只需要比较到倒
数第二个位置即可,此时次大的记录被放在了倒数第二个位置,直到比较完成。
注意到,较大的记录被放在了后面,娇小的记录被放在了前面,这跟水中冒泡一样,较重的物体下
沉,而水泡上浮。
故被称作:“冒泡法”。
示例
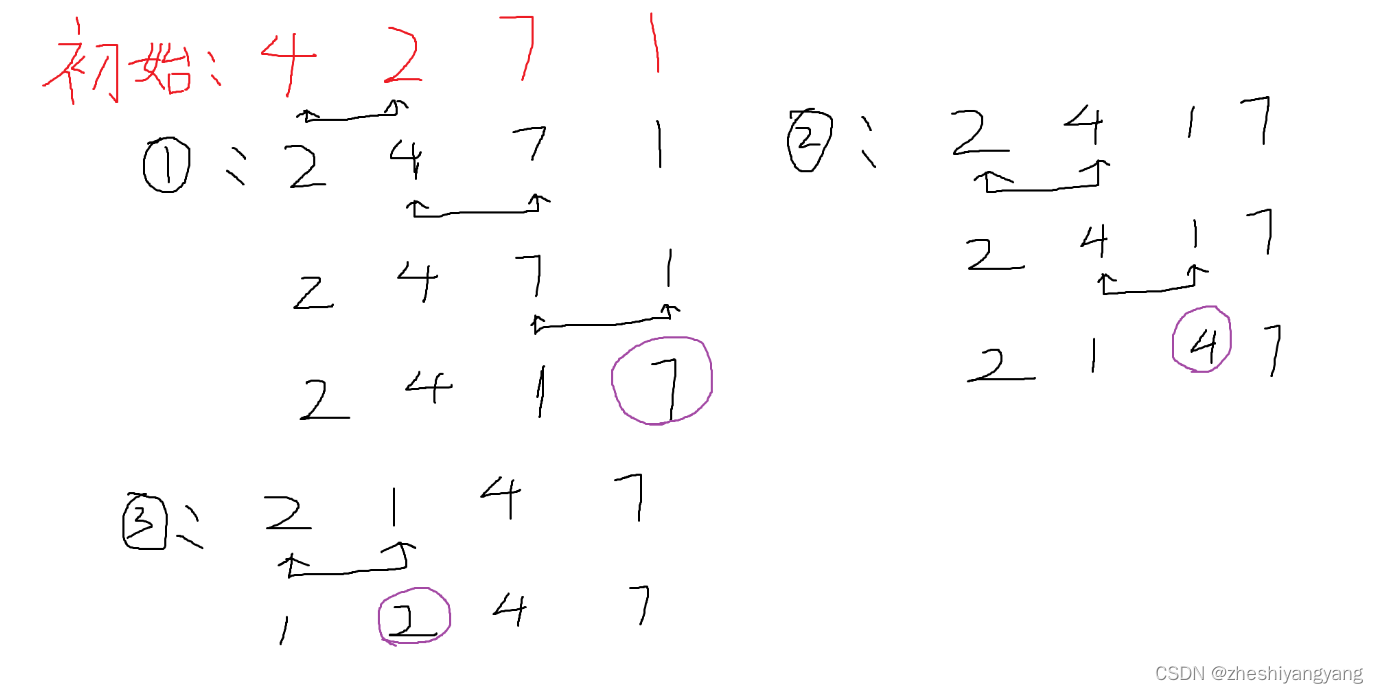
代码
OrderList BubbleSort(OrderList L)
{
RecordType tmp;
int i,j;
for(i=1;i<=L.length-1;i++){
for(j=1;j<=L.length-i;j++){
if(L.data[j].key > L.data[j+1].key){
tmp = L.data[j];
L.data[j] = L.data[j+1];
L.data[j+1] = tmp;
}
}
}
return L;
}快速排序
基本思想
从待排序的N个记录中,取第一个记录作为枢纽记录,所有比枢纽记录小的记录放在左侧,比枢纽
记录大的记录放在右侧。然后对两边的两个字表重新进行快速排序(选择枢纽记录)。
直到每个子表的长度不大于1为止。
示例


代码
int Partition(OrderList *L,int i,int j) //对当前i->j范围内的记录做一次快速排序
{
KeyType pivotkey;
L->data[0] = L->data[i];
pivotkey = L->data[i].key;
while(i<j){
while(i<j&&L->data[j].key>=pivotkey)
j--;
L->data[i] = L->data[j];
while(i<j&&L->data[i].key<=pivotkey)
i++;
L->data[j] = L->data[i];
}
L->data[i] = L->data[0];
return i;
}
void QuickSort(OrderList *L,int i,int j) //递归快速排序
{
int pivotkey;
if(i<j){
pivotkey = Partition(L,i,j);
QuickSort(L,i,pivotkey-1);
QuickSort(L,pivotkey+1,j);
}
}
总代码
#include<stdio.h>
#define MAX 100
typedef int KeyType;
typedef struct{
KeyType key;
}RecordType;
typedef struct{
RecordType data[MAX];
int length;
}OrderList;
OrderList BubbleSort(OrderList L)
{
RecordType tmp;
int i,j;
for(i=1;i<=L.length-1;i++){
for(j=1;j<=L.length-i;j++){
if(L.data[j].key > L.data[j+1].key){
tmp = L.data[j];
L.data[j] = L.data[j+1];
L.data[j+1] = tmp;
}
}
}
return L;
}
int Partition(OrderList *L,int i,int j) //对当前i->j范围内的记录做一次快速排序
{
KeyType pivotkey;
L->data[0] = L->data[i];
pivotkey = L->data[i].key;
while(i<j){
while(i<j&&L->data[j].key>=pivotkey)
j--;
L->data[i] = L->data[j];
while(i<j&&L->data[i].key<=pivotkey)
i++;
L->data[j] = L->data[i];
}
L->data[i] = L->data[0];
return i;
}
void QuickSort(OrderList *L,int i,int j) //递归快速排序
{
int pivotkey;
if(i<j){
pivotkey = Partition(L,i,j);
QuickSort(L,i,pivotkey-1);
QuickSort(L,pivotkey+1,j);
}
}
int main()
{
int simple[11] = {-1,5,9,1,100,56,78,22,40,60,99};
int i;
OrderList L;
L.length = 10;
for(i=1;i<11;i++)
L.data[i].key = simple[i];
//L = BubbleSort(L); 冒泡排序
//QuickSort(&L,1,10); 快速排序
for(i=1;i<11;i++)
printf("%d ",L.data[i].key);
return 0;
}