1、求解矩阵连乘问题。
要求:
分别用自底向上的动态规划方法和自顶向下的备忘录方法计算最优值并构造最优解,通过实例比较两种方法的结果和效率。
思路
1)寻找最优子结构:
此问题最难就在于此,对于乘积的任意位置加括号都会将序列在某个地方分成两部分,也就是最后一次乘法计算的地方,及这个位置为K,也就是先计算(A1...Ak)(Ak+1...An),然后两部分结果相乘。
2)构造递归解
设m[i,j]为矩阵链Ai…Aj的最优解的代价。A[i:j]表示AiAi+1...Aj
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数为m[i,j],则原问题的最优值为m[1,n]
当 i = j 时,A[i:j]=Ai,因此,m[i,i]=0,i=1,2,…,n
当 i < j时,若A[i:j]的最优次序在Ak和Ak+1间断开,
3)构建辅助表,解决重叠子问题
从第二步的递归式可以发现解的过程中会有很多重叠子问题,可以用一个n*n维的辅助表m[n][n] 和 s[n][n],分别表示最优乘积代价及其分割位置k
辅助表s[n][n]可以由2种方法构造:
一种是自底向上填表构建,该方法要求按照递增的方式逐步填写子问题的解,也就是先计算长度为2的所有矩阵链的解,然后计算长度3的矩阵链,直到长度n;
另一种是自顶向下填表的备忘录法,该方法将表的每个元素初始化为某特殊值(本问题中可以将最优乘积代价设置为一极大值),以表示待计算,在递归的过程中逐个填入遇到的子问题的解。
自底向上的动态规划:
1找出最优解性质,刻画结构特征
2.自底向上的方式计算最优解
3.根据计算最优解时得到的信息,构造最优解
void MatrixChain(int n)
{
int r, j;
for (int i = 0; i <= n; i++) {
m[i][i] = 0;
}
for ( r = 2; r <= n; r++) {
for (int i = 1; i <= n - r + 1; i++) {
j = i + r - 1;
m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (int k = i + 1; k < j; k++) {
int temp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (temp < m[i][j]) {
s[i][j] = k;
m[i][j] = temp;
}
}
}
}
}从上向下的备忘录方法:
int lookup_chain(int p[], int n, int m[][N], int s[][N], int i, int j) { if (m[i][j] < INT_MAX) { return m[i][j]; } if (i == j) { m[i][j] = 0; } else { for (int k = i; k <= j - 1; k++) { int q = lookup_chain(p, n, m, s, i, k) + lookup_chain(p, n, m, s, k + 1, j) + p[i - 1] * p[k] * p[j]; if (q < m[i][j]) { m[i][j] = q; s[i][j] = k; } } } return m[i][j]; }
实验结果
动态规划
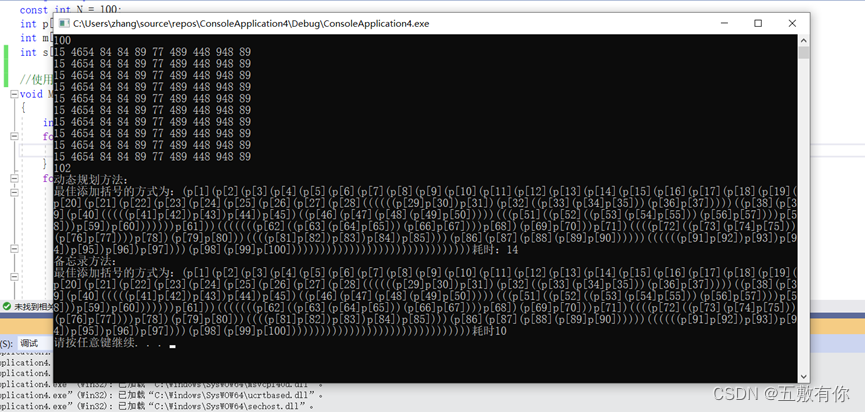
备忘录方法: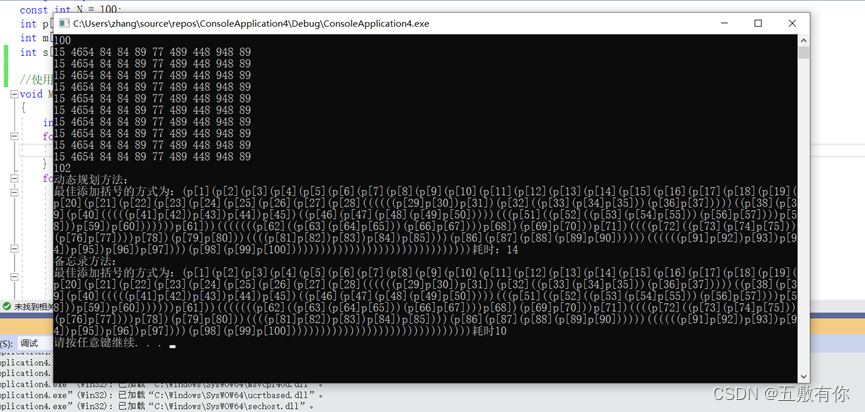
对比发现:
用了100个矩阵相乘多次验证,结果是备忘录方法快,查看了资料发现,数据量足够小,自顶向下的备忘录方法可能会更快一些,因为它可以利用备忘录表中已经计算过的结果,减少重复计算的开销。而自底向上的动态规划方法则需要计算所有子问题,并将结果存储在表中,即使某些子问题在后续计算中不需要再次使用,仍然需要计算和存储。