数据结构——链式二叉树的实现（详解）

呀哈喽。我是结衣。
不知道大家的递归学到怎么样呢？如果大家的递归功底不是很好，那么我相信在学完这篇文章后大家一定会对递归有一个更深层次的了解的。

构造链式二叉树

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

结构体的创建

typedef int BTdatatype;
typedef struct BinaryTreeNode
{
	BTdatatype data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}Treenode;

相信学了那么多数据结构的大家一定对此不会陌生，这里的结构体的创建的链表是相似的，毕竟这里的二叉树也是链式结构的。

函数的声明

Treenode* BTTreeCreat(BTdatatype x);
//前序
void PreOrder(Treenode* root);
//中序
void MidOrder(Treenode* root);
//求树的节点个数
int treesize(Treenode* root);
//求叶节点的个数
int TreeLeafSize(Treenode* root);
//求树的高度
int Treehight(Treenode* root);
//第k层的节点个数
int TreeLevelK(Treenode* root, int k);
//销毁
void treeDestroy(Treenode* root);
//查找
Treenode* BinaryTreeFind(Treenode*root,BTdatatype x);

没错学习二叉树就是为了让我们能够实现上面的功能。

构建二叉树

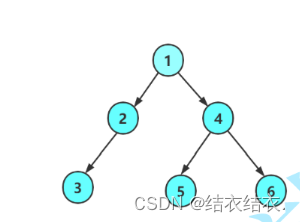
就想前文讲到的那样，现在我先面向结果构造一个如下图所示的二叉树出来，降低学习的成本，然后运用这棵树来实现二叉树的功能。
在这里插入图片描述

创造节点

Treenode* BTTreeCreat(BTdatatype x)
{
	Treenode* newnode = (Treenode*)malloc(sizeof(Treenode));
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

这个节点的创造和链表一模一样。不懂的小伙伴可以去看我实现链表的那篇文章。
节点创建完了，我们直接面向结果构造一个二叉树（如上图）

Treenode* root1 = BTTreeCreat(1);
	Treenode* root2 = BTTreeCreat(2);
	Treenode* root3 = BTTreeCreat(3);
	Treenode* root4 = BTTreeCreat(4);
	Treenode* root5 = BTTreeCreat(5);
	Treenode* root6 = BTTreeCreat(6);
	//Treenode* root7 = BTTreeCreat(7);
	root1->left = root2;
	root1->right = root4;
	root2->left = root3;
	root4->left = root5;
	root4->right = root6;
	//root5->right = root7;

构造完这个二叉树后我们就要来逐一的实现他的功能了。

函数的实现

我们要实现的功能有：打印二叉树的前序、中序，求二叉树的节点个数，求二叉树的叶节点个数，求二叉树的高度，求第k层的节点个数。

二叉树前序遍历

在实现这功能之前，我们先来了解一下上面是前序、中序、后序：

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
简洁一点就是
前序的访问顺序为根左右
中序的访问顺序为左根右
后序的访问顺序为左右根
了解完毕，看代码

void PreOrder(Treenode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
	{
		printf("%d ", root->data);
		PreOrder(root->left);
		PreOrder(root->right);
	}
}

发现是递归了吗？没错要实现链式二叉树的遍历就是要用递归的。我们来分析一下这个代码：
递归的结束条件 节点为空时就返回。
在这里插入图片描述
当我们进入函数1时，肯定是直接进入else中然后打印1，往下走，将root的左子树传入同函数，第二次进函数2打印2，再将2的左子树传进函数，再进入函数3打印3。这里要注意了，3的左子树为空，所以我们进入函数4的if里面打印N，然后再返回函数3，返回函数3后由于函数3还没执行完就继续往下执行，将3的右子树传给函数3-1，为空打印N，然后返回函数3此时函数3执行完毕退出函数3到函数2。后面差不多就略了，我们来画图看看。
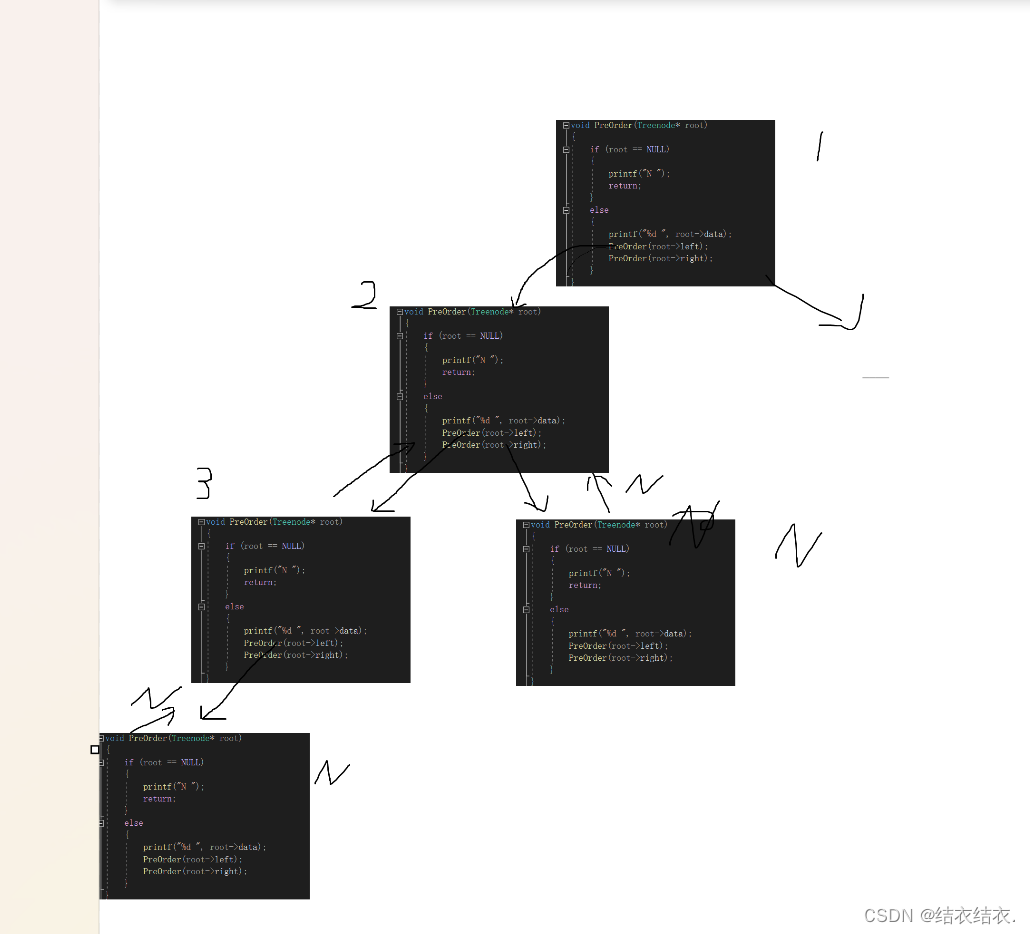
在这里插入图片描述
就是这么调用的。
下面看看打印效果

和我们分析的一样。

中序遍历

中序遍历只需要把打印放再中间就可以了。

void MidOrder(Treenode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
	{
		MidOrder(root->left);
		printf("%d ", root->data);
		MidOrder(root->right);
	}
}

在这里插入图片描述
这就是它的打印结果大家可以自己分析分析。

求树的节点个数

求节点的个数，我们肯定就要遍历二叉树，所以肯定要用到递归（下面的函数实现也都要用到递归）
首先我们要确定递归的返回条件，当节点为空时我们就返回，并且我要返回0.

int treesize(Treenode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return treesize(root->left) + treesize(root->right) + 1;
}

这个代码的本质其实就是，如果该节点不为空就加1，为空就加0。因为在我们调用的每个函数里面只要不是空节点，那么它就会加1然后返回，假设我们已经进入3节点了，当我们继续执行函数的时候，它将3的左右子树再次进入函数，因为左右子树为0。返回0回到3节点再加1回到节点2然后同上。最后我们就能遍历二叉树求的节点的个数了。

在这里插入图片描述

求叶节点的个数

叶节点就是指：没有左右子树的节点。
实现前我们肯定要确定递归停止的条件。当节点为空时返回0。那么我们应该知道当当叶节点进入函数的时候叶要返回，这次返回1。然后就是递归调用。

int TreeLeafSize(Treenode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (!root->left && !root->right)
		return 1;
	else
		return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

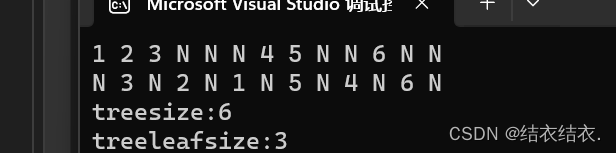
在这里插入图片描述
打印结果也是没有问题的。

求树的高度

要想求树的高度，我们可以这要求：

int Treehight(Treenode* root)
{
	if (root == NULL)
		return 0;
	int lefthight = Treehight(root->left) + 1;
	int righthight = Treehight(root->right) + 1;
	return lefthight > righthight ? lefthight : righthight;

	/*int lefthight = Treehight(root->left);
	int righthight = Treehight(root->right);
	return lefthight > righthight ? lefthight+1: righthight+1;*/

	//return fmax()
}

求树的高度本质上就是找最长的一条线路，我们利用lefthight来保存左边最长的线路，用righthight来保存右边最长的线路，最后利用三目操作符的性质来返回最长的一条线路。
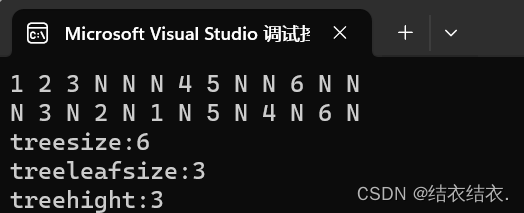
在这里插入图片描述
我们还可以再加一个节点7放在5节点的右边再验证一次。

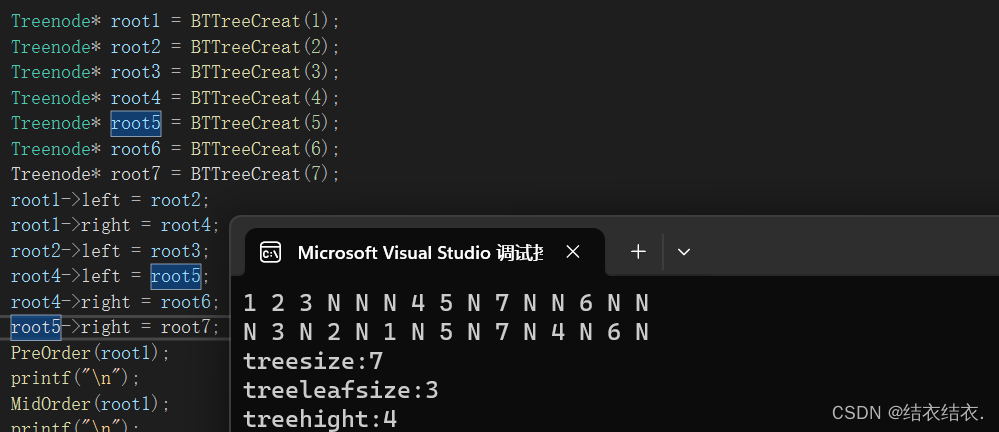
事实上没有问题。

求第k层的节点个数

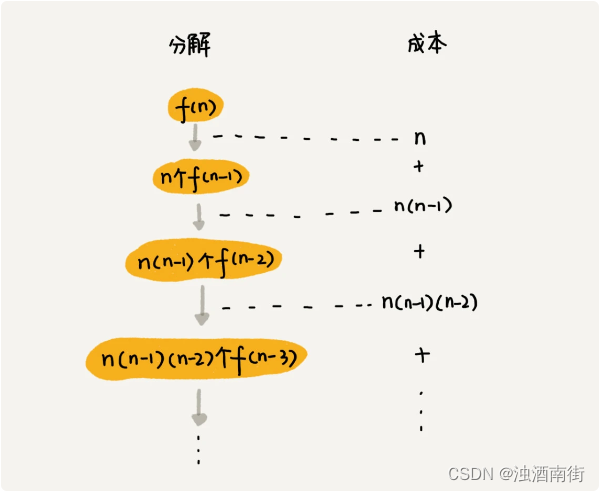
这个可以说是我们目前实现函数里面最难想到的一种了。首先我们要想怎么把他拆分成一个个的子问题。再把那个图取过来看看。
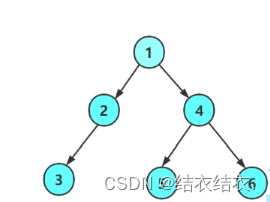
在这里插入图片描述
假设我们要求的是第3层节点的个数，是不是可以转换成2，3节点的第二层。3，5，6节点的第一层。有了这个思路来实现起来就会变得容易了。

int TreeLevelK(Treenode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	else
		return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);

}

我们通过将k不断地减小，将问题的难度逐渐的压缩。最终得到一个不能再压缩的子问题，这就是递归的本质！
看看实现的效果。
我们来求第3层的节点个数（前文我加了一个节点进去，所以二叉树一共是有7个节点的）
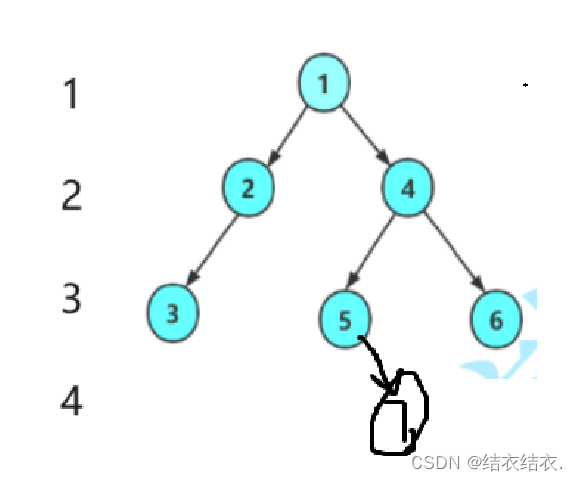
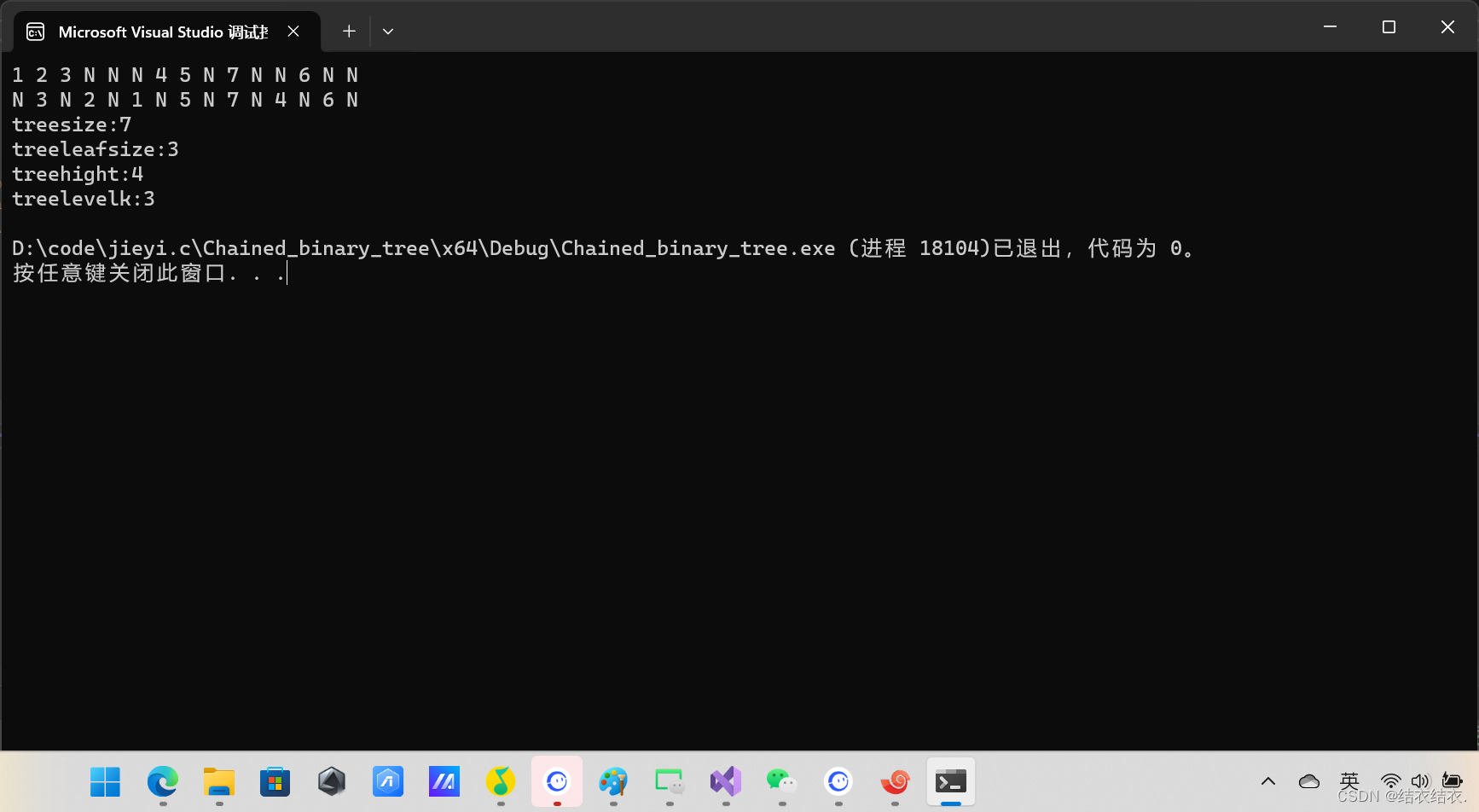
在这里插入图片描述

在这里插入图片描述
没有问题，下面我就把我的原码放再下面了

代码

tree.h

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#include <math.h>
typedef int BTdatatype;
typedef struct BinaryTreeNode
{
	BTdatatype data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}Treenode;

Treenode* BTTreeCreat(BTdatatype x);
//前序
void PreOrder(Treenode* root);
//中序
void MidOrder(Treenode* root);
//求树的节点个数
int treesize(Treenode* root);
//求叶节点的个数
int TreeLeafSize(Treenode* root);
//求树的高度
int Treehight(Treenode* root);
//第k层的节点个数
int TreeLevelK(Treenode* root, int k);
//销毁
void treeDestroy(Treenode* root);

tree.c

#define _CRT_SECURE_NO_WARNINGS
#include "tree.h"

Treenode* BTTreeCreat(BTdatatype x)
{
	Treenode* newnode = (Treenode*)malloc(sizeof(Treenode));
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}
void treeDestroy(Treenode* root)
{
	assert(root);
	
}
void PreOrder(Treenode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
	{
		printf("%d ", root->data);
		PreOrder(root->left);
		PreOrder(root->right);
	}
}
void MidOrder(Treenode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
	{
		MidOrder(root->left);
		printf("%d ", root->data);
		MidOrder(root->right);
	}
}

int treesize(Treenode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return treesize(root->left) + treesize(root->right) + 1;
}

int TreeLeafSize(Treenode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (!root->left && !root->right)
		return 1;
	else
		return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int Treehight(Treenode* root)
{
	if (root == NULL)
		return 0;
	int lefthight = Treehight(root->left) + 1;
	int righthight = Treehight(root->right) + 1;
	return lefthight > righthight ? lefthight : righthight;

	/*int lefthight = Treehight(root->left);
	int righthight = Treehight(root->right);
	return lefthight > righthight ? lefthight+1: righthight+1;*/

	//return fmax()
}

int TreeLevelK(Treenode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	else
		return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);

}

test.c

#include "tree.h"



int main()
{
	Treenode* root1 = BTTreeCreat(1);
	Treenode* root2 = BTTreeCreat(2);
	Treenode* root3 = BTTreeCreat(3);
	Treenode* root4 = BTTreeCreat(4);
	Treenode* root5 = BTTreeCreat(5);
	Treenode* root6 = BTTreeCreat(6);
	Treenode* root7 = BTTreeCreat(7);
	root1->left = root2;
	root1->right = root4;
	root2->left = root3;
	root4->left = root5;
	root4->right = root6;
	root5->right = root7;
	PreOrder(root1);
	printf("\n");
	MidOrder(root1);
	printf("\n");
	printf("treesize:%d", treesize(root1));
	printf("\n");
	printf("treeleafsize:%d\n", TreeLeafSize(root1));
	printf("treehight:%d\n", Treehight(root1));
	printf("treelevelk:%d\n", TreeLevelK(root1, 3));
	
	return 0;
}